Exercices - Géométrie dans l'espace

Géométrie dans l'espace

Exercice 1 : Étude de droites et de points dans un repère orthogonal

L'espace est rapporté au repère orthogonal $(O, \vec{i}, \vec{j}, \vec{k})$. Les points $A$, $B$ et $C$ ont pour coordonnées respectives $A(1; -1; 2)$, $B(3; 3; 8)$, $C(-3; 5; 4)$.

On considère les droites $D_1$ et $D_2$ définies par leurs représentations paramétriques :

$D_1 : \begin{cases} x = 2 + t \\ y = -1 + 2t \\ z = -4 + 3t \end{cases} , t \in \mathbb{R}$

$D_2 : \begin{cases} x = 3 + k \\ y = -1 + 2k \\ z = -4 + 3k \end{cases} , k \in \mathbb{R}$

Et la droite $D_3$ définie par sa représentation paramétrique :

$D_3 : \begin{cases} x = 4 - 4t \\ y = 3 - 3t \\ z = 2 + 3t \end{cases} , t \in \mathbb{R}$

Pour chacune des affirmations suivantes, indiquez si elle est vraie ou fausse en justifiant rigoureusement votre réponse.

Affirmation 1 : Les droites $D_1$ et $D_2$ sont parallèles.
Affirmation 2 : Le point $E$ de la droite $D_2$ dont l'abscisse est 3 a pour cote 1.
Affirmation 3 : Le point $C$ appartient à la droite $D_1$.
Affirmation 4 : Les droites $D_3$ et $D_1$ sont sécantes.

Correction :

Affirmation 1 : Les droites $D_1$ et $D_2$ sont parallèles.

Les vecteurs directeurs de $D_1$ et $D_2$ sont respectivement $\vec{u_1} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$ et $\vec{u_2} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$.

Méthode 1 : Proportionnalité des coordonnées

On observe que les coordonnées des vecteurs $\vec{u_1}$ et $\vec{u_2}$ sont proportionnelles (en fait, elles sont égales). Cela signifie que $\vec{u_1} = 1 \cdot \vec{u_2}$.

Méthode 2 : Recherche de k

On cherche un réel $k$ tel que $\vec{u_1} = k \vec{u_2}$. Dans ce cas, il est évident que $k=1$ convient.

Puisque les vecteurs directeurs sont colinéaires, les droites $D_1$ et $D_2$ sont parallèles. L'affirmation est donc vraie.

Affirmation 2 : Le point $E$ de la droite $D_2$ dont l'abscisse est 3 a pour cote 1.

Si l'abscisse de $E$ est 3, alors $3 = 3 + k$, donc $k = 0$. Les coordonnées de $E$ sont alors $(3; -1 + 2(0); -4 + 3(0)) = (3; -1; -4)$.

La cote de $E$ est -4, et non 1. L'affirmation est donc fausse.

Affirmation 3 : Le point $C$ appartient à la droite $D_1$.

$C(-3; 5; 4)$ appartient à $D_1$ si et seulement si il existe un réel $t$ tel que :

$\begin{cases} -3 = 2 + t \\ 5 = -1 + 2t \\ 4 = -4 + 3t \end{cases}$

On résout chaque équation séparément : $\begin{cases} t = -5 \\ t = 3 \\ t = \frac{8}{3} \end{cases}$

Le système n'a pas de solution commune, donc $C$ n'appartient pas à $D_1$. L'affirmation est donc fausse.

Affirmation 4 : Les droites $D_3$ et $D_1$ sont sécantes.

Pour déterminer si les droites $D_1$ et $D_3$ sont sécantes, on cherche s'il existe des valeurs de $t$ et $k$ telles que :

$\begin{cases} 2 + t = 4 - 4k \\ -1 + 2t = 3 - 3k \\ -4 + 3t = 2 + 3k \end{cases}$

On peut résoudre ce système d'équations. De la première équation, on a $t = 2 - 4k$. Substituons dans la deuxième équation :

$-1 + 2(2 - 4k) = 3 - 3k \implies -1 + 4 - 8k = 3 - 3k \implies 3 - 8k $

=$ 3 - 3k \implies -8k = -3k \implies 5k = 0$

\implies k = 0$

Si $k = 0$, alors $t = 2 - 4(0) = 2$. Vérifions si ces valeurs satisfont la troisième équation :

$-4 + 3(2) = 2 + 3(0) \implies -4 + 6 = 2 \implies 2 = 2$, ce qui est vrai.

Ainsi, les droites $D_1$ et $D_3$ sont sécantes. L'affirmation est donc vraie.

Exercice 2 : Étude d'un cube dans un repère orthonormé

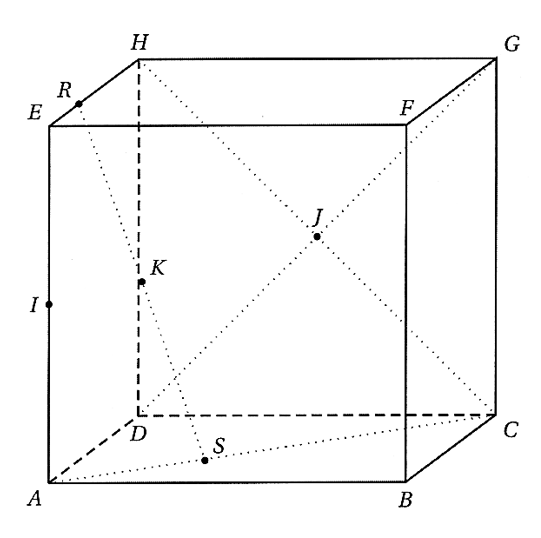
On considère le cube $ABCDEFGH$ de côté 1. On note $I$ le milieu de $[AE]$, $J$ le milieu de $[DG]$. $R$ et $S$ sont définis par $\vec{ER} = \frac{1}{3}\vec{EH}$ et $\vec{AS} = \frac{1}{3}\vec{AC}$. $K$ est le milieu du segment $[RS]$. On se place dans le repère $(A, \vec{AB}, \vec{AD}, \vec{AE})$.

Justifiez par des calculs que $I(0, 0, \frac{1}{2})$ et $J(\frac{1}{2}, \frac{1}{2}, 1)$.
Déterminez une représentation paramétrique de la droite $(IJ)$.
Justifiez par des calculs que $R(0, \frac{1}{3}, 1)$ et $S(\frac{1}{3}, \frac{1}{3}, 0)$.
a. Déterminez les coordonnées du point $K$.

b. Démontrez que les points $I$, $K$ et $J$ sont alignés.
En déduire que les points $I$, $K$, $J$, $R$ et $S$ sont coplanaires.

Correction :

Question 1 : Justification des coordonnées de $I$ et $J$.

$I$ est le milieu du segment $[AE]$. Pour trouver les coordonnées de $I$, on applique la formule du milieu : on prend la moyenne des coordonnées de $A$ et de $E$.

Les coordonnées de $A$ sont $(0,0,0)$ et celles de $E$ sont $(0,0,1)$. Donc, les coordonnées de $I$ sont :

$x_I = \frac{x_A + x_E}{2} = \frac{0 + 0}{2} = 0$

$y_I = \frac{y_A + y_E}{2} = \frac{0 + 0}{2} = 0$

$z_I = \frac{z_A + z_E}{2} = \frac{0 + 1}{2} = \frac{1}{2}$

Par conséquent, $I(0, 0, \frac{1}{2})$.

De même, $J$ est le milieu de $[DG]$. Les coordonnées de $D$ sont $(0,1,0)$ et celles de $G$ sont $(1,1,1)$. En utilisant la formule du milieu, les coordonnées de $J$ sont données par :

$x_J = \frac{x_D + x_G}{2} = \frac{0 + 1}{2} = \frac{1}{2}$

$y_J = \frac{y_D + y_G}{2} = \frac{1 + 1}{2} = 1$

$z_J = \frac{z_D + z_G}{2} = \frac{0 + 1}{2} = \frac{1}{2}$

Par conséquent, $J(\frac{1}{2}, 1, \frac{1}{2})$.

Question 2 : Représentation paramétrique de $(IJ)$.

$\vec{IJ} = \vec{AJ} - \vec{AI} = (\frac{1}{2}, \frac{1}{2}, 1) - (0, 0, \frac{1}{2}) = (\frac{1}{2}, \frac{1}{2}, \frac{1}{2})$.

Donc, une représentation paramétrique de $(IJ)$ est : $\begin{cases} x = 0 + \frac{1}{2}t \\ y = 0 + \frac{1}{2}t \\ z = \frac{1}{2} + \frac{1}{2}t \end{cases} , t \in \mathbb{R}$

Question 3 : Justification des coordonnées de $R$ et $S$.

$\vec{ER} = \frac{1}{3}\vec{EH}$, donc $\vec{AR} = \vec{AE} + \vec{ER} = \vec{AE} + \frac{1}{3}\vec{EH} = \vec{AE} + \frac{1}{3}\vec{AD}$. Ainsi, les coordonnées de $R$ sont $(0, \frac{1}{3}, 1)$.

$\vec{AS} = \frac{1}{3}\vec{AC} = \frac{1}{3}(\vec{AB} + \vec{AD})$. Ainsi, les coordonnées de $S$ sont $(\frac{1}{3}, \frac{1}{3}, 0)$.

Question 4 :

a. Coordonnées de $K$.

$K$ est le milieu de $[RS]$, donc $K = (\frac{x_R + x_S}{2}, \frac{y_R + y_S}{2}, \frac{z_R + z_S}{2}) = (\frac{0 + \frac{1}{3}}{2}, \frac{\frac{1}{3} + \frac{1}{3}}{2}, \frac{1 + 0}{2}) = (\frac{1}{6}, \frac{1}{3}, \frac{1}{2})$.

b. Démontrez que les points $I$, $K$ et $J$ sont alignés.

Pour montrer que les points $I$, $K$ et $J$ sont alignés, nous allons montrer que les vecteurs $\vec{IK}$ et $\vec{IJ}$ sont colinéaires.

On a : $\vec{IK} = \vec{AK} - \vec{AI} = (\frac{1}{6}, \frac{1}{3}, \frac{1}{2}) - (0, 0, \frac{1}{2}) = (\frac{1}{6}, \frac{1}{3}, 0)$

Et : $\vec{IJ} = \vec{AJ} - \vec{AI} = (\frac{1}{2}, \frac{1}{2}, 1) - (0, 0, \frac{1}{2}) = (\frac{1}{2}, \frac{1}{2}, \frac{1}{2})$

Méthode 1 : Proportionnalité des coordonnées

On vérifie s'il existe un scalaire $k$ tel que $\vec{IK} = k \vec{IJ}$. Cela reviendrait à dire que : $(\frac{1}{6}, \frac{1}{3}, 0) = k (\frac{1}{2}, \frac{1}{2}, \frac{1}{2})$

En comparant les troisièmes coordonnées, on aurait $0 = k \cdot \frac{1}{2}$, ce qui implique $k=0$. Mais si $k=0$, alors les premières et deuxièmes coordonnées de $\vec{IK}$ devraient aussi être nulles, ce qui n'est pas le cas. Donc, il n'existe pas de tel $k$, et les vecteurs ne sont pas colinéaires.

Méthode 2 : Recherche de k

Cherchons $k$ tel que $\vec{IK} = k\vec{IJ}$ : $(\frac{1}{6}, \frac{1}{3}, 0) = k(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}) \implies \begin{cases} \frac{1}{6} = \frac{1}{2}k \\ \frac{1}{3} = \frac{1}{2}k \\ 0 = \frac{1}{2}k \end{cases}$

La troisième équation implique $k = 0$, ce qui contredit les deux premières. Donc, $\vec{IK}$ et $\vec{IJ}$ ne sont pas colinéaires. Par conséquent, les points $I, K, J$ ne sont pas alignés.

Question 5 : Les points $I$, $K$, $J$, $R$ et $S$ sont coplanaires.

Les points $I$, $J$, $R$ et $S$ appartiennent au même plan. De plus, les droites (IJ) et (RS) ne sont pas parallèles, mais elles sont coplanaires. Comme K appartient aux deux droites (par définition, K est le milieu de \[RS] et on sait que K est sur la droite (IJ)), les droites (IJ) et (RS) sont sécantes en K. Conclusion, les points $I, K, J, R, S$ sont coplanaires