Fonctions Trigonométriques
Exercice 1 : Calcul d'aire
Fonction trigonométrique
On considère la fonction $f$ définie sur $[0;2\pi]$ par
$f(x)=-1.5\cos(x)+1.5$.
On admet que la fonction $f$ est continue sur $[0;2\pi]$.
On note $\mathcal{C}_{1}$ la courbe représentative de la fonction $f$ dans un repère orthonormé.
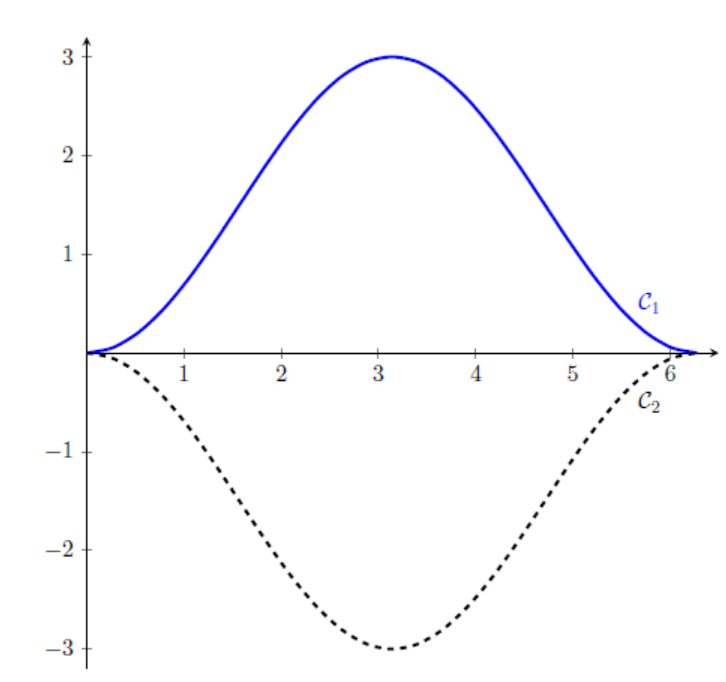
Courbe de la fonction $f$
1) Démontrer que la fonction $f$ est positive sur $[0 ; 2\pi]$.
2) Sur la figure ci-dessus, la courbe tracée en tiretés, notée $\mathcal{C}_{2}$, est la courbe
symétrique de $\mathcal{C}_{1}$ par rapport à l’axe des abscisses.
La forme d’un carreau est celle de la zone délimitée par les courbes $\mathcal{C}_{1}$ et
$\mathcal{C}_{2}$.
On note $\mathcal{A}$ son aire, exprimée en unité d’aire.
Calculer $\mathcal{A}$.
Exercice 2 : Étude d'une fonction et calcul d'aire
Un publicitaire souhaite imprimer le logo ci-dessous sur un T-shirt :
Il dessine ce logo à l’aide des courbes de deux fonctions $f$ et $g$ définies sur $\mathbb{R}$
par :
$f(x)=e^{-x}(-\cos(x)+\sin(x)+1)$
et
$g(x)=-e^{-x}\cos(x)$.
On admet que les fonctions $f$ et $g$ sont dérivables sur $\mathbb{R}$.
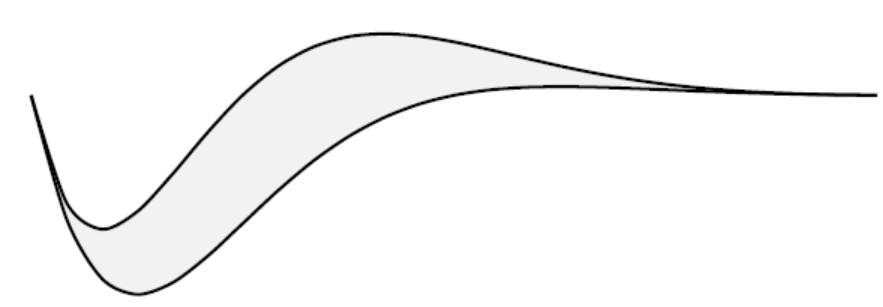
Logo
Partie A : Étude de la fonction $f$
1) Justifier que, pour tout $x\in \mathbb{R}$ :
$-e^{-x} \leq f(x) \leq 3e^{-x}$.
2) En déduire la limite de $f$ en $+\infty$.
3) Démontrer que, pour tout $x \in \mathbb{R}$, $f'(x) = e^{-x}(2\cos(x) - 1)$ où $f'$ est la fonction dérivée de $f$.
4) Dans cette question, on étudie la fonction $f$ sur l’intervalle $[-\pi;\pi]$.
a) Déterminer le signe de $f'(x)$ pour $x$ appartenant à l’intervalle $[-\pi;\pi]$.
b) En déduire les variations de $f$ sur $[-\pi;\pi]$.
Partie B : Aire du logo
On note $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$ les représentations graphiques des fonctions
$f$ et $g$ dans un repère orthonormé $(O;\vec{i},\vec{j})$.
L’unité graphique est de 2 centimètres.
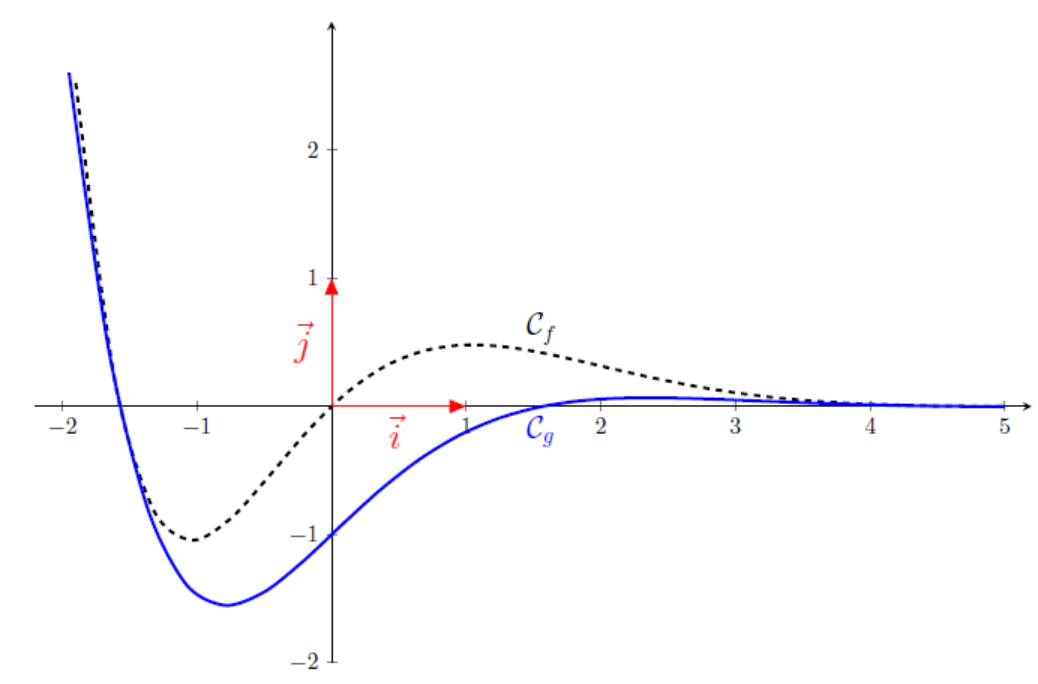
Courbe de la fonction $f$et $g$
1) Étudier la position relative de la courbe $\mathcal{C}_{f}$ par rapport à la courbe $\mathcal{C}_{g}$ sur $\mathbb{R}$.
2) Soit $H$ la fonction définie sur $\mathbb{R}$ par : $H(x)=(-\frac{\cos x}{2}-\frac{\sin x}{2}-1)e^{-x}$. On admet que $H$ est une primitive de la fonction $x \mapsto (\sin x+1)e^{-x}$ sur $\mathbb{R}$. On note $\mathcal{D}$ le domaine délimité par la courbe $\mathcal{C}_{f}$, la courbe $\mathcal{C}_{g}$ et les droites d’équation $x=-\frac{\pi}{2}$ et $x=\frac{3\pi}{2}$.
a) Hachurer le domaine $\mathcal{D}$ sur le graphique à rendre avec la copie.
b) Calculer, en unité d’aire, l’aire du domaine $\mathcal{D}$, puis en donner une valeur approchée à $10^{-2}$ près en cm2.
Exercice 3 : Optimisation d'angle
Lors d’un match de rugby, un joueur doit transformer un essai qui a été marqué au point $E$
(voir figure ci-contre) situé à l’extérieur du segment $[AB]$.
La transformation consiste à taper le ballon par un coup de pied depuis un point $T$ que le
joueur a le droit de choisir n’importe où sur le segment $[EM]$ perpendiculaire à la droite
$(AB)$ sauf en $E$. La transformation est réussie si le ballon passe entre les poteaux
repérés par les points $A$ et $B$ sur la figure.
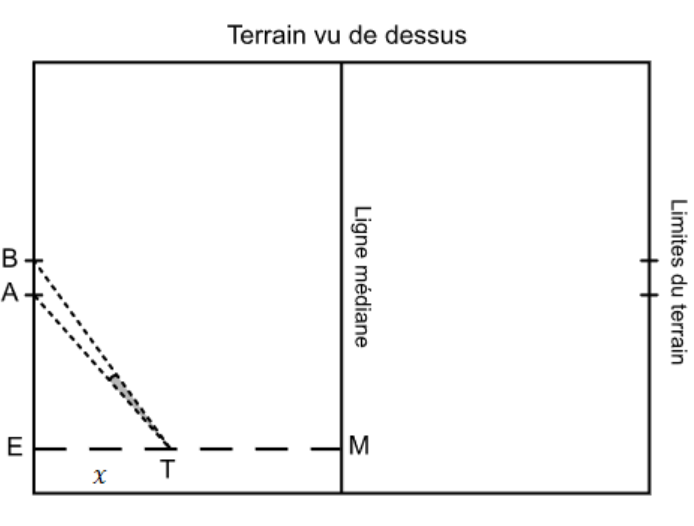
Courbe de la fonction $f$
Le but de cet exercice est donc de rechercher s’il existe une position du point $T$ sur le segment $[EM]$ pour laquelle l’angle $\widehat{ATB}$ est maximum et, si c’est le cas, de déterminer une valeur approchée de cet angle.
Dans toute la suite, on note $x$ la longueur $ET$, qu’on cherche à déterminer.
Les dimensions du terrain sont les suivantes : $EM = 50\text{ m}$, $EA = 25\text{ m}$ et $AB = 5,6\text{ m}$. On note $\alpha$ la mesure en radian de l’angle $\widehat{ETA}$, $\beta$ la mesure en radian de l’angle $\widehat{ETB}$ et $\gamma$ la mesure en radian de l’angle $\widehat{ATB}$.
1) En utilisant les triangles rectangles $ETA$ et $ETB$ ainsi que les longueurs fournies, exprimer $\tan\alpha$ et $\tan\beta$ en fonction de $x$. La fonction tangente est définie sur l’intervalle $]0 ;\frac{\pi}{2}[$ par $\tan x=\frac{\sin x}{\cos x}$.
2) Montrer que la fonction $\tan$ est strictement croissante sur l’intervalle $]0 ;\frac{\pi}{2}[$.
3) L’angle $\widehat{ATB}$ admet une mesure $\gamma$ appartenant à l’intervalle $]0 ;\frac{\pi}{2}[$, résultat admis ici, que l’on peut observer sur la figure. On admet que, pour tous réels $a$ et $b$ de l’intervalle $]0 ;\frac{\pi}{2}[$, $\tan(a-b)=\frac{\tan a-\tan b}{1+\tan a \times \tan b}$. Montrer que $\tan \gamma=\frac{5.6x}{x^{2}+765}$.
4) L’angle $\widehat{ATB}$ est maximum lorsque sa mesure $\gamma$ est maximale. Montrer que cela correspond à un minimum sur l’intervalle $]0; 50]$ de la fonction $f$ définie par : $f(x)=x+\frac{765}{x}$. Montrer qu’il existe une unique valeur de $x$ pour laquelle l'angle $\widehat{ATB}$ est maximum et déterminer cette valeur de $x$ au mètre près ainsi qu’une mesure de l'angle $\widehat{ATB}$ à 0.01 radian près.
Exercice 4 : Étude de fonctions et calcul d'aire
Partie B
Dans cette partie, on admet que, pour tout réel $\theta$,
$\cos(\theta)+\sin(\theta)=\sqrt{2}\cos \left(\theta−\frac{\pi}{4}\right)$.
On considère les fonctions $f$ et $g$ définies sur l’intervalle $[0 ;+\infty[$ par :
$f(x)=e^{-x}\cos(x)$
et
$g(x)=e^{-x}$.
On définit la fonction $h$ sur $[0 ;+\infty[$ par $h(x)=g(x)−f(x)$.
Les représentations graphiques $\mathscr{C}_{f}$, $\mathscr{C}_{g}$ et
$\mathscr{C}_{h}$ des fonctions $f$, $g$ et $h$ sont données ci-dessous, dans un repère
orthogonal.
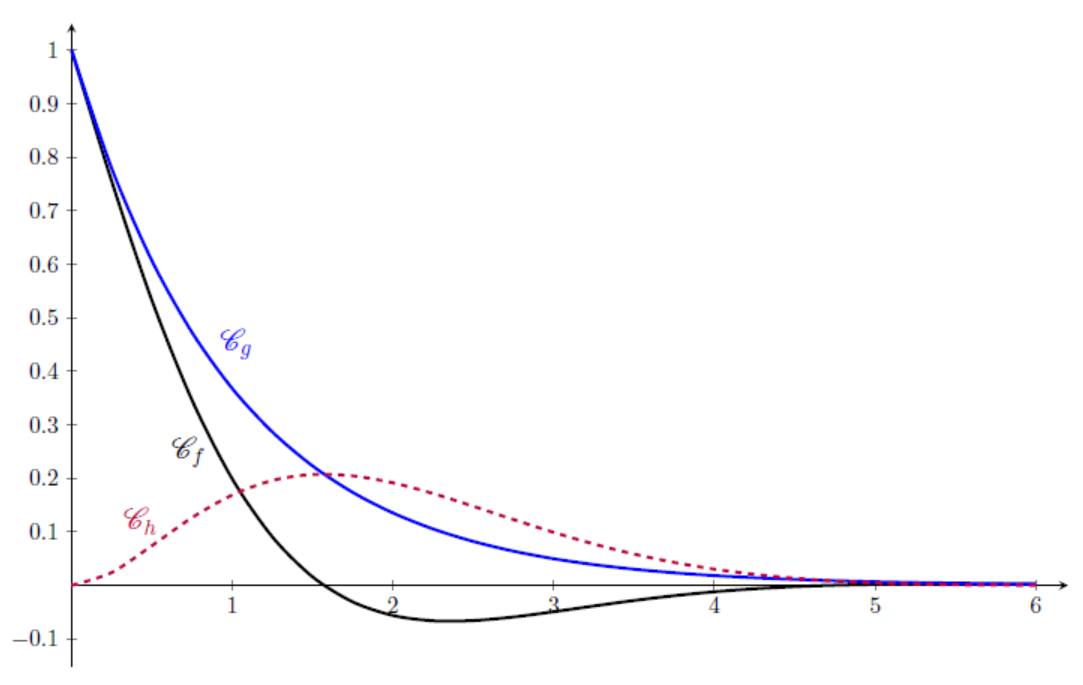
Schéma $f$
1) Conjecturer :
a) les limites des fonctions $f$ et $g$ en $+\infty$ ;
b) la position relative de $\mathscr{C}_{f}$ par rapport à $\mathscr{C}_{g}$ ;
c) la valeur de l’abscisse $x$ pour laquelle l’écart entre les deux courbes
$\mathscr{C}_{f}$ et $\mathscr{C}_{g}$ est maximal.
2) Justifier que $\mathscr{C}_{g}$ est située au-dessus de $\mathscr{C}_{f}$ sur l’intervalle $[0 ;+\infty[$.
3) Démontrer que la droite d’équation $y=0$ est asymptote horizontale aux courbes $\mathscr{C}_{f}$ et $\mathscr{C}_{g}$.
4) a) On note $h'$ la fonction dérivée de la fonction $h$ sur l’intervalle $[0 ;+\infty[$. Démontrer que, pour tout $x$ de l’intervalle $[0 ;+\infty[$, $h'(x)=e^{-x}\left[\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\right]$.
b) Justifier que, sur l’intervalle $\left[0;\frac{\pi}{2}\right]$, $\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\geq 0$ et que, sur l'intervalle $\left[\frac{\pi}{2};2\pi\right]$, $\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)-1\leq 0$.
c) En déduire le tableau de variation de la fonction $h$ sur l’intervalle $[0 ; 2\pi]$.
5) On admet que, sur l’intervalle $[0 ;+\infty[$, la fonction $H$ définie par $H(x)=\frac{1}{2}e^{-x}\left[-2+\cos(x)-\sin(x)\right]$ est une primitive de la fonction $h$. On note $\mathscr{D}$ le domaine du plan délimité par les courbes $\mathscr{C}_{f}$ et $\mathscr{C}_{g}$, et les droites d’équations $x=0$ et $x=2\pi$. Calculer l’aire $\mathscr{A}$ du domaine $\mathscr{D}$, exprimée en unités d’aire.
Exercice 5 : Calcul d'aire
Partie C
Le service commercial a adopté pour les étiquettes des bouteilles la forme représentée
ci-dessous dans un repère orthonormé du plan.
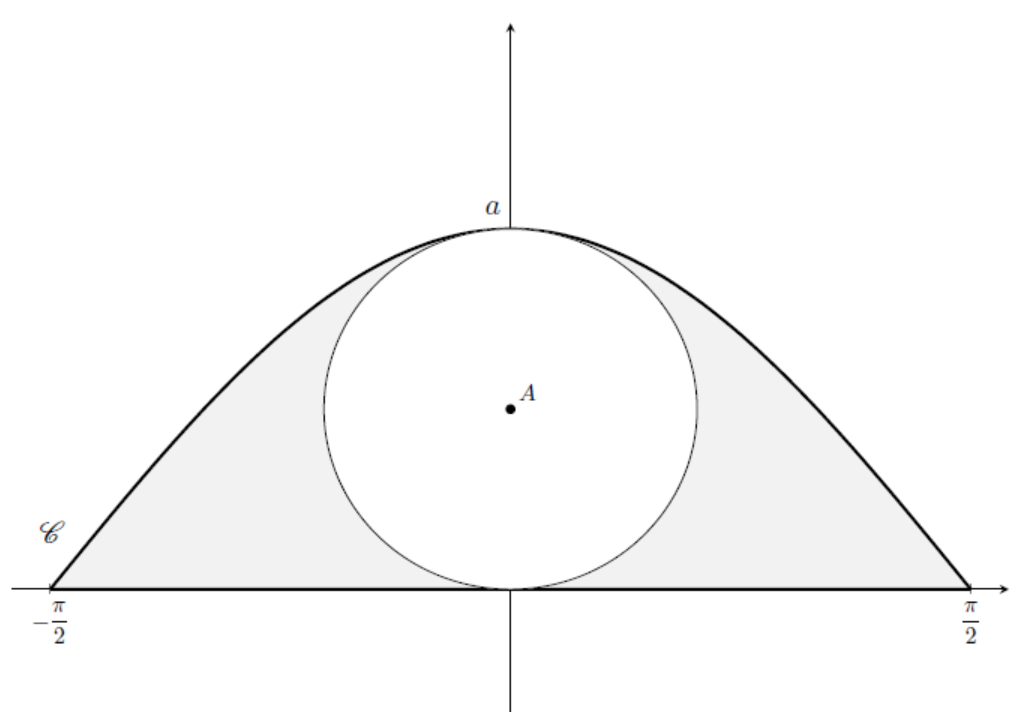
Schéma $f$
La forme de ces étiquettes est délimitée par l’axe des abscisses et la courbe $\mathscr{C}$ d’équation $y=a\cos x$ avec $x \in \left[−\frac{\pi}{2};\frac{\pi}{2}\right]$ et $a$ un réel strictement positif. Un disque situé à l’intérieur est destiné à recevoir les informations données aux acheteurs. On considère le disque de centre le point $A$ de coordonnées $\left(0 ;\frac{a}{2}\right)$ et de rayon $\frac{a}{2}$. On admettra que ce disque se trouve entièrement en dessous de la courbe $\mathscr{C}$ pour des valeurs de $a$ inférieures à 1,4.
1) Justifier que l’aire du domaine compris entre l’axe des abscisses, les droites d’équation $x=-\frac{\pi}{2}$ et $x=\frac{\pi}{2}$, et la courbe $\mathscr{C}$ est égale à $2a$ unités d’aire.
2) Pour des raisons esthétiques, on souhaite que l’aire du disque soit égale à l’aire de la surface grisée. Quelle valeur faut-il donner au réel $a$ pour respecter cette contrainte ?