Fonctions Trigonométriques
Exercice 1 : Fonction impaire et périodique
Soit $f$ une fonction définie sur $\mathbb{R}$, impaire et périodique de période 4 telle que
$f(-1)=3$. Parmi les nombres suivants, lesquels peut‑on déterminer ? Justifier.
1. $f(0)$
2. $f(1)$
3. $f(2)$
4. $f(3)$
Exercice 2 : Restriction d'étude
Soit $f$ une fonction définie sur $\mathbb{R}$, impaire et périodique de période 4. Sur quel intervalle peut‑on restreindre son étude ?
Exercice 3 : Compléter une courbe
Compléter la courbe $\mathcal{C}_f$ ci‑dessous, représentative d'une fonction $f$ impaire et définie sur $[-8; 8]$. (Image à insérer)
Exercice 4 : Courbes et conditions
Tracer dans chaque cas, si possible, la courbe représentative d'une fonction $f$ définie
sur $\mathbb{R}$ respectant les conditions données. Justifier lorsque c'est impossible.
1. $f$ est à la fois paire et impaire.
2. $f$ est paire et strictement croissante.
3. $f$ est impaire et strictement décroissante.
Exercice 5 : Périodicité
Dans chaque cas, tracer, si possible, la courbe représentative d'une fonction $f$ définie
sur $\mathbb{R}$ respectant les conditions données. Justifier lorsque c'est impossible.
1. $f$ est périodique de période 1 mais non de période 2.
2. $f$ est périodique de période 2 mais non de période 1.
3. $f$ est périodique de périodes 2 et 3.
Exercice 6 : Vrai / Faux
Parmi les affirmations suivantes, trouver celles qui sont toujours vraies. Justifier
1. Si $f$ n'est pas paire, alors elle est impaire.
2. Si $f$ est paire, alors elle ne peut pas être impaire.
3. Si $f$ est périodique, alors elle est définie sur $\mathbb{R}$.
4. Si $f(3)=f(-3)=-f(-3)$, alors $f$ est à la fois paire et impaire.
5. Si $f$ est définie en 3 mais pas en -3, alors $f$ n'est ni paire ni impaire.
6. Si $f$ est périodique de période 3, alors elle est périodique de période 6.
7. Si $f$ est périodique de période 6, alors elle est périodique de période 3.
8. Si $f$ est impaire, alors $f$ est définie en 0 et $f(0)=0$.
9. Si $f$ est impaire et périodique de période 3, alors on peut restreindre son étude à
$[-1,5; 0]$.
10. Si $f$ est impaire et périodique de période 3 avec $f(-1)=2$, alors $f(4)=-2$.
Exercice 7 : Fonction impaire et périodique
1. Compléter le tracé ci‑dessous sur $[-2,5; 5]$, sachant que $f$ est une fonction définie
sur $\mathbb{R}$, impaire et périodique de période 4.
(Image à insérer)
2. Résoudre dans $\mathbb{R}$ l'équation $f(x)=0$. Justifier.
Exercice 8 : Fonction impaire et périodique
Soit $f$ la fonction définie sur $\mathbb{R}$, impaire et périodique de période 4 telle
que :
sur $[-1; 0]$, $f(x) = x$ ;
sur $]1; 2]$, $f(x) = (x-2)^2$.
1. Déterminer $f(-4,5)$ ; $f(-1,5)$ et $f(7)$.
2. Montrer que $f$ est continue en 1.
3. Construire le tableau de variations de $f$ sur $[-5; 3]$. On pourra s'aider d'un tracé.
Exercice 9 : Vrai / Faux
Soit $f$ une fonction définie sur $\mathbb{R}$ à la fois paire et périodique de période
2. Donner, en justifiant, les propositions qui sont toujours vraies.
1. $f(0) = 0$
2. $f(5) = -f(5)$
3. $f(5) = f(-5)$
4. $f(5) = 0$
Exercice 10 : Parité de fonctions
Dans chaque cas, étudier la parité de la fonction $f$ définie sur $\mathbb{R}$ par :
1. $f(x) = \frac{e^x + e^x}{2}$
2. $f(x) = \frac{e^x - e^x}{2}$
3. $f(x) = \frac{e^x + e^{-x}}{2}$ (appelée cosinus hyperbolique)
4. $f(x) = \frac{e^x - e^{-x}}{2}$ (appelée sinus hyperbolique)
Exercice 11 : Fonction périodique
Soit $f$ une fonction définie sur $\mathbb{R}$, périodique de période 4 et telle que,
sur $[0; 4]$, l'équation $f(x)=0$ a pour solutions 1 et 2,5.
1. Résoudre $f(x)=0$ sur $\mathbb{R}$. Justifier.
2. Pour quelle raison $f$ ne peut‑elle pas être impaire ?
3. Pour quelle raison $f$ ne peut‑elle pas être paire ?
Exercice 12 : Dérivées et propriétés
Soient $f$ une fonction définie et dérivable sur $\mathbb{R}$ et $T$ un réel strictement
positif.
1. Déterminer, en fonction de $f'$, la dérivée des fonctions $g: x \mapsto f(-x)$ ; $h: x
\mapsto -f(x)$ et $k: x \mapsto f(x+T)$.
2. Montrer que si $f$ est paire, alors $f'$ est impaire.
3. Montrer que si $f$ est impaire, alors $f'$ est paire.
4. Montrer que si $f$ est périodique de période $T$, alors $f'$ est aussi périodique de
période $T$.
Exercice 13 : Association de courbes
Associer à chacune des courbes $\mathcal{C}_1$, $\mathcal{C}_2$ et $\mathcal{C}_3$ tracées ci‑dessous la fonction qui lui correspond parmi : $f: x \mapsto x \sin(x)$ ; $g: x \mapsto x^2 \sin(x)$ et $h: x \mapsto x \sin^2(x)$. Justifier.
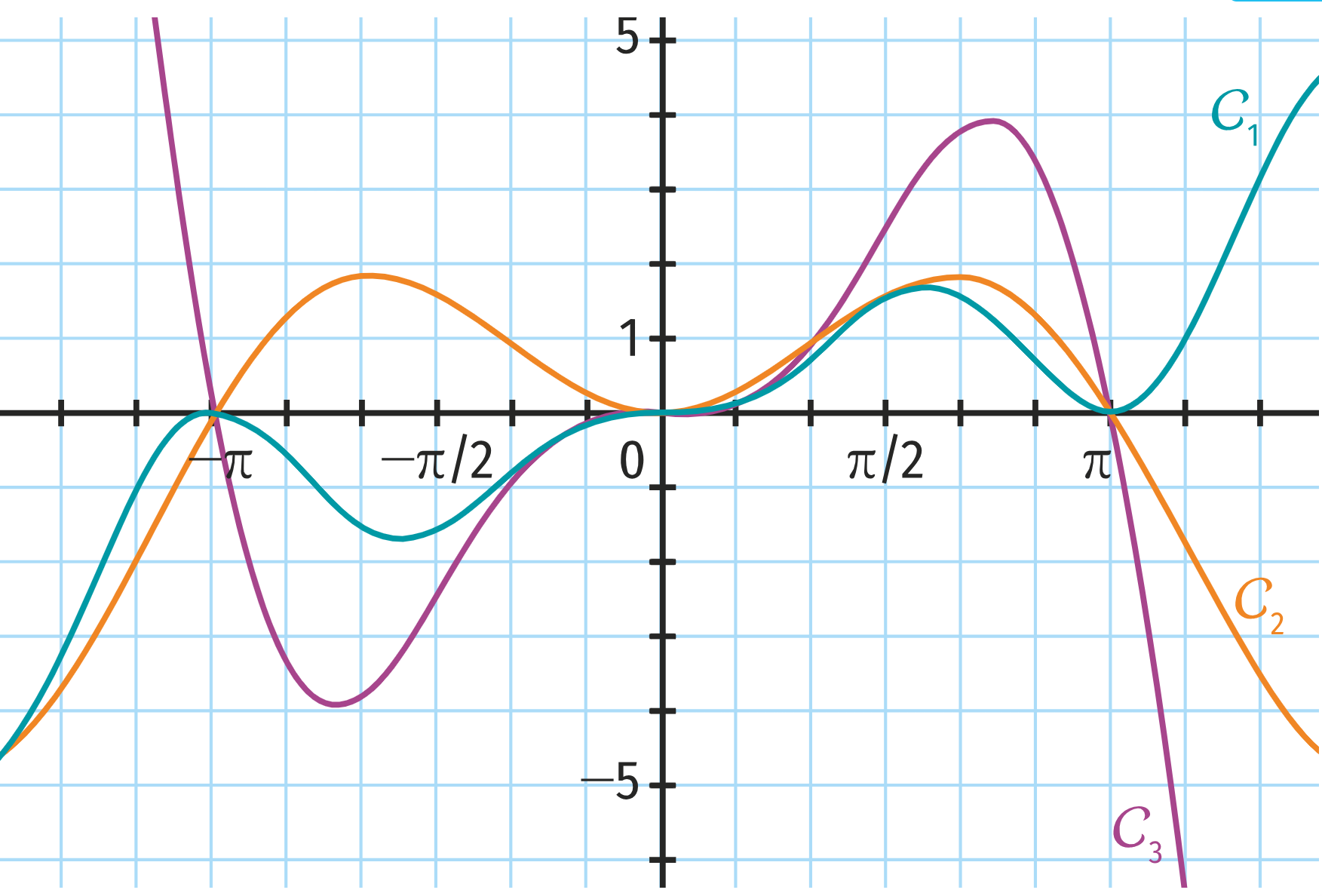
Courbes $f$
Exercice 14 : Association de courbes
Associer à chacune des courbes $\mathcal{C}_1$, $\mathcal{C}_2$ et $\mathcal{C}_3$ tracées ci‑dessous la fonction qui lui correspond parmi : $f: x \mapsto \sin(\frac{x}{2})$ ; $g: x \mapsto \sin(x)$ et $h: x \mapsto \sin(2x)$. Justifier.
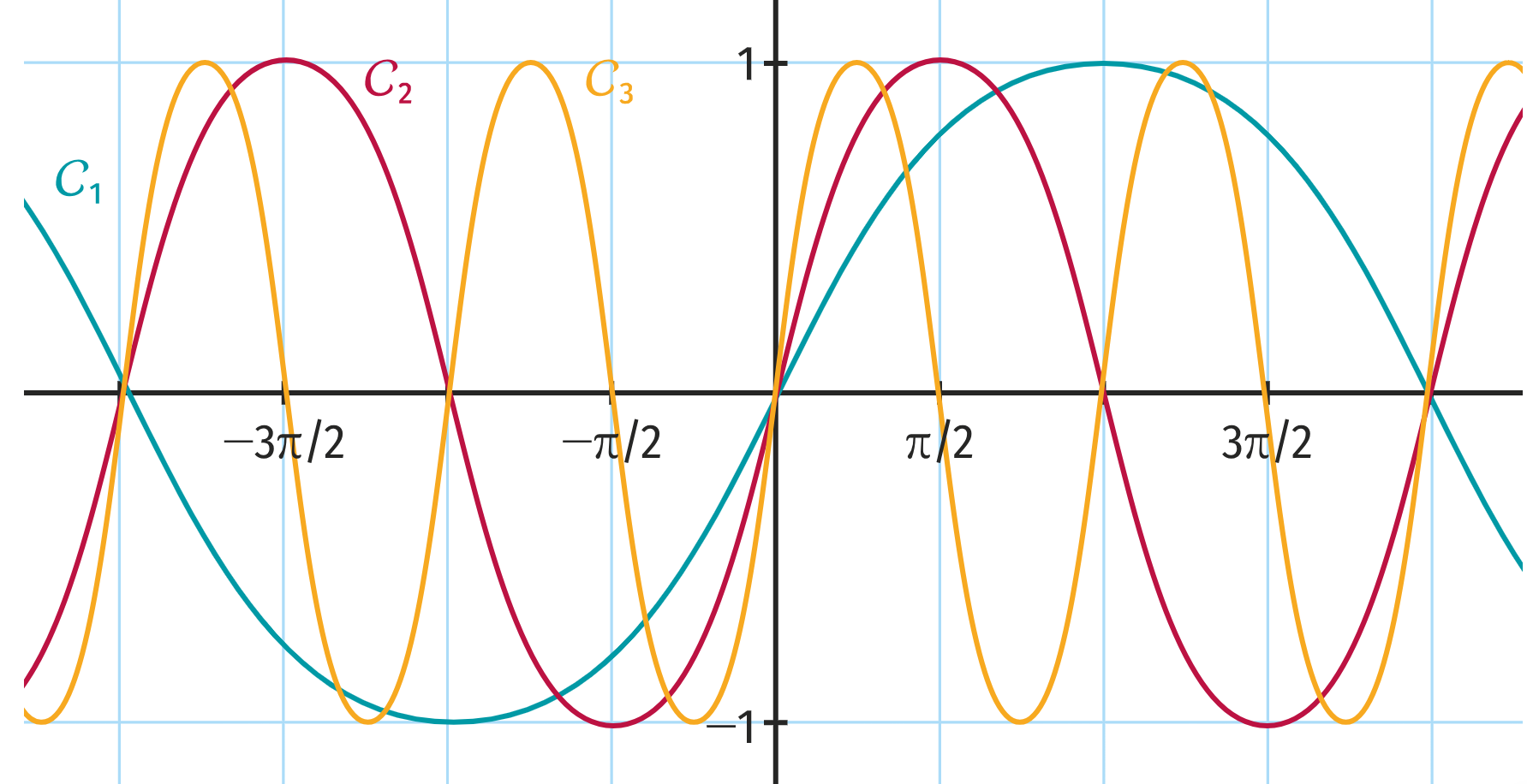
Courbes $f$
Exercice 15 : Fonction et sa dérivée
On a tracé ci‑dessous deux courbes $\mathcal{C}_1$ et $\mathcal{C}_2$. L'une des deux
représente une fonction $f$ et l'autre sa fonction dérivée $f'$.
1. Laquelle des deux représente la fonction $f$ ? Justifier.
2. Déterminer la plus petite des périodes de $f$.
3. Déterminer la plus petite des périodes de $f'$.
Exercice 16 : Fonction périodique
Soit $s$ la fonction définie pour tout $t \in \mathbb{R}$ par :
$s(t) = 2\cos(\frac{2\pi t}{7}) - 2\sin(\frac{2\pi t}{7}) - \cos(\frac{4\pi t}{7}) +
4\sin(\frac{4\pi t}{7})$.
Montrer que $s$ est une fonction périodique de période 7.
Exercice 17: Calculatrice et radians/degrés
Yann se souvient que $\cos(\frac{\pi}{4}) = \sin(\frac{\pi}{4})$. Expliquer pourquoi sa calculatrice lui affiche alors $\cos(\frac{\pi}{4}) \approx 0,9999060498$ et $\sin(\frac{\pi}{4}) \approx 0,0137073546$.
Exercice 18 : Placer des angles sur le cercle trigonométrique
Comment placer très simplement et précisément les réels $\frac{\pi}{6}$, $\frac{\pi}{4}$ et $\frac{\pi}{3}$ sur un cercle trigonométrique ?
Exercice 19 : Variations de la fonction sinus
1. Par simple lecture graphique sur un cercle trigonométrique, déterminer, sur $[0; \pi]$,
les variations de la fonction $\sin$.
2. Après avoir rappelé les propriétés de parité et de périodicité de $\sin$, construire le
tableau de variations de $\sin$ sur $[-2\pi; 2\pi]$.
Exercice 20 : Variations de la fonction cosinus
1. Par simple lecture graphique sur un cercle trigonométrique, déterminer, sur $[0; \pi]$,
les variations de la fonction $\cos$.
2. Après avoir rappelé les propriétés de parité et de périodicité de $\cos$, construire le
tableau de variations de $\cos$ sur $[-2\pi; 2\pi]$.
Exercice 21 : Équations trigonométriques
Résoudre sur $\mathbb{R}$ les équations suivantes.
1. $\sin(x) = -1$
2. $\cos(x) = -1$
3. $\sin(x) = -0,5$
4. $\cos(x) = -0,5$
Exercice 22 : Inéquations trigonométriques
Résoudre sur $[-\pi; \pi]$ les inéquations suivantes.
1. $\sin(x) < -0,5$
2. $\cos(x) > 0,5$
3. $\sin(x) \geq -2$
4. $\cos(x) \leq -2$
Exercice 23 : Inéquation trigonométrique
À la question « résoudre dans $[-\pi; \pi]$ l'inéquation $\sin(x) \geq -0,5$ », Étienne a répondu $[-\frac{5\pi}{6}; -\frac{\pi}{6}]$ alors que son amie Rachida a répondu $[-\frac{\pi}{6}; -\frac{5\pi}{6}]$. Mehdi pense qu'ils se sont tous les deux trompés. Déterminer celui des trois qui a raison. Justifier.
Exercice 24 : Comparaison de cosinus
Sans utiliser de calculatrice et en justifiant le résultat, classer par ordre croissant les nombres suivants : $\cos(\frac{\pi}{5})$ ; $\cos(\frac{\pi}{7})$ ; $\cos(\frac{2\pi}{5})$ ; $\cos(\frac{3\pi}{5})$ et $\cos(\frac{3\pi}{7})$.
Exercice 25 : Comparaison de sinus
Sans utiliser de calculatrice et en justifiant le résultat, classer par ordre croissant les nombres suivants : $\sin(\frac{\pi}{5})$ ; $\sin(\frac{\pi}{7})$ ; $\sin(\frac{2\pi}{5})$ ; $\sin(\frac{3\pi}{5})$ et $\sin(\frac{3\pi}{7})$.
Exercice 26 : Comparaison de sinus et cosinus
Sans utiliser de calculatrice et en justifiant le résultat, classer par ordre croissant les nombres suivants : $\sin(\frac{\pi}{5})$ ; $\sin(\frac{\pi}{7})$ ; $\cos(\frac{\pi}{5})$ et $\cos(\frac{\pi}{7})$.
Exercice 27 : Fonction trigonométrique
Soit $f$ la fonction définie sur $\mathbb{R}$ par : $f(x)=2 \cos \left(\frac{3 x}{\pi}\right)-3 \sin ^{2}\left(\frac{4 x}{\pi}\right)+1$.
1. Uniquement à l'aide de la calculatrice et sans justifier :
a. préciser si $f(0) = -2$ ;
b. préciser si $f\left(\frac{\pi^{2}}{6}\right)=\frac{-5}{4}$ ;
c. préciser si $f$ est paire ou impaire ;
d. préciser si $f$ est périodique de période $2\pi$ ;
e. déterminer le nombre de solutions sur $[-2\pi~; 2\pi]$ de l'équation $f(x) = 0$ ;
f. déterminer la limite éventuelle de $f(x)$ en $+\infty$ ;
g. préciser si $f'(0)=0$ ;
h. préciser si $f'\left(\frac{\pi^{2}}{6}\right)=\frac{-12}{\pi}$.
2. Préciser si sa dérivée $f'$ est définie sur $\mathbb{R}$ par $f^{\prime}(x)=\frac{-6}{\pi} \sin \left(\frac{3 x}{\pi}\right)-\frac{12}{\pi} \sin \left(\frac{8 x}{\pi}\right)$.
Exercice 28 : Fonction trigonométrique
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=2 \cos (2 x)-1$.
1. Résoudre dans $\mathbb{R}$ l'équation $f(x) = 0$.
2. Déterminer la plus petite période $T$ de $f$.
3. Montrer qu'il est possible de restreindre l'étude de $f$ à $\left[0; \frac{\pi}{2}\right]$.
4. Démontrer que sur $\left[0 ; \frac{\pi}{2}\right]$, $f^{\prime}(x) \leqslant 0$.
5. Construire le tableau de variations de $f$ sur $[-\pi; \pi]$.
Exercice 29
Partie A
La courbe suivante représente sur $[-\pi; \pi]$ la fonction $f$ définie par $f(x) = ax + b\cos(x) + c$.
Déterminer les réels $a$, $b$ et $c$, sachant que la tangente à la courbe au point $A$ d'abscisse $-\frac{\pi}{2}$ est horizontale et que celle au point $B$ de coordonnées $(0; 3)$ a pour coefficient directeur $-2$.
Partie B
Soit $g$ la fonction définie sur $\mathbb{R}$ par :
$g(x) = -2x + 2\cos(x) + 1$.
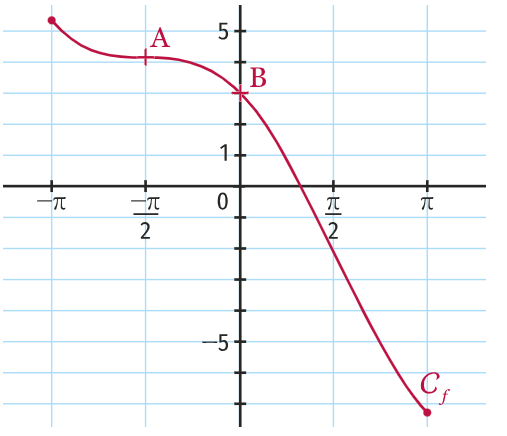
Courbes $f$
2. Montrer que sur $[0; \frac{\pi}{2}]$, l'équation $g(x) = 0$ admet une unique solution $\alpha$ et encadrer $\alpha$ au dixième.
3. En déduire le signe de $g(x)$ sur $\mathbb{R}$.
Exercice 30 : Fonction trigonométrique
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)= \sin (2 x)-1$.
1. Résoudre dans $\mathbb{R}$ l'équation $f(x) = 0$.
2. Déterminer la plus petite période $T$ de $f$.
3. Montrer qu'il est possible de restreindre l'étude de $f$ à $\left[0; \frac{\pi}{2}\right]$.
4. Démontrer que sur $\left[0 ; \frac{\pi}{2}\right]$, $f^{\prime}(x) \geqslant 0$.
5. Construire le tableau de variations de $f$ sur $[-\pi; \pi]$.
Exercice 31 : Fonction trigonométrique
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)= \frac{1}{2}\cos (4 x)+\frac{1}{2}$.
1. Résoudre dans $\mathbb{R}$ l'équation $f(x) = 0$.
2. Déterminer la plus petite période $T$ de $f$.
3. Montrer qu'il est possible de restreindre l'étude de $f$ à $\left[0; \frac{\pi}{4}\right]$.
4. Démontrer que sur $\left[0 ; \frac{\pi}{4}\right]$, $f^{\prime}(x) \leqslant 0$.
5. Construire le tableau de variations de $f$ sur $[-\pi; \pi]$.
Exercice 32 : Fonction trigonométrique
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)= 4\sin (3x)$.
1. Résoudre dans $\mathbb{R}$ l'équation $f(x) = 0$.
2. Déterminer la plus petite période $T$ de $f$.
3. Montrer qu'il est possible de restreindre l'étude de $f$ à $\left[0; \frac{\pi}{3}\right]$.
4. Démontrer que sur $\left[0 ; \frac{\pi}{6}\right]$, $f^{\prime}(x) \geq 0$ et sur $\left[\frac{\pi}{6} ; \frac{\pi}{3}\right]$, $f^{\prime}(x) \leq 0$.
5. Construire le tableau de variations de $f$ sur $[-\pi; \pi]$.
Exercice 33 : Fonction trigonométrique
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)= -3\cos (2x+\frac{\pi}{3})$.
1. Résoudre dans $\mathbb{R}$ l'équation $f(x) = 0$.
2. Déterminer la plus petite période $T$ de $f$.
3. Montrer qu'il est possible de restreindre l'étude de $f$ à $\left[-\frac{\pi}{6}; \frac{\pi}{3}\right]$.
4. Démontrer que sur $\left[-\frac{\pi}{6} ; \frac{\pi}{12}\right]$, $f^{\prime}(x) \geq 0$ et sur $\left[\frac{\pi}{12} ; \frac{\pi}{3}\right]$, $f^{\prime}(x) \leq 0$.
5. Construire le tableau de variations de $f$ sur $[-\pi; \pi]$.
Exercice 34 : Fonction trigonométrique
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)= 2\cos (3x-\frac{\pi}{4})+3$.
1. Résoudre dans $\mathbb{R}$ l'équation $f(x) = 3$.
2. Déterminer la plus petite période $T$ de $f$.
3. Montrer qu'il est possible de restreindre l'étude de $f$ à $\left[0; \frac{\pi}{3}\right]$.
4. Démontrer que sur $\left[0 ; \frac{\pi}{4}\right]$, $f^{\prime}(x) \leq 0$ et sur $\left[\frac{\pi}{4} ; \frac{\pi}{3}\right]$, $f^{\prime}(x)$ change de signe.
5. Construire le tableau de variations de $f$ sur $[-\pi; \pi]$.
Exercice 35 : Équation trigonométrique
Résoudre dans $\mathbb{R}$ l'équation $\cos(2x) + \sin(x) = 0$.
Exercice 36 : Inéquation trigonométrique
Résoudre dans $[-\pi; \pi]$ l'inéquation $\sin(3x) \leq \frac{\sqrt{3}}{2}$.
Exercice 37 : Parité et périodicité
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = \cos(2x) - \sin(3x)$.
1. Déterminer la parité de $f$.
2. Montrer que $f$ est périodique et déterminer sa période.
Exercice 38 : Dérivée et variations
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = x + \sin(x)$.
1. Calculer $f'(x)$.
2. Montrer que pour tout $x \in \mathbb{R}$, $f'(x) \geq 0$.
3. En déduire les variations de $f$ sur $\mathbb{R}$.
Exercice 39 : Fonction trigonométrique et tangente
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = \sin(x)$.
1. Donner l'équation de la tangente à la courbe représentative de $f$ au point d'abscisse $0$.
2. Montrer que pour tout $x \geq 0$, $\sin(x) \leq x$.
3. Que peut-on dire de la position relative de la courbe et de sa tangente en $0$ ?
Exercice 40 : Encadrement d'une fonction trigonométrique
Montrer que pour tout $x \in \mathbb{R}$, on a : $$-\sqrt{2} \leq \sin(x) + \cos(x) \leq \sqrt{2}$$
Exercice 41 : Limite trigonométrique
Calculer la limite suivante : $$\lim_{x \to 0} \frac{\sin(3x)}{\sin(5x)}$$
Exercice 42 : Identité trigonométrique
Démontrer l'identité trigonométrique suivante : $$\cos^2(x) - \sin^2(x) = \cos(2x)$$
Exercice 43 : Équation trigonométrique
Résoudre dans $\mathbb{R}$ l'équation $\tan(x) = \sqrt{3}$.