Exercices de base dans l'espace
Exercice 1
Dans un repère orthonormé de l'espace, on considère les points $A(2, 1, 3)$, $B(4, 3, 1)$, $C(1, 5, 2)$ et $D(-1, 3, 4)$.
- Calculer les coordonnées des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$.
- Calculer les normes des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$.
- Calculer le produit scalaire $\overrightarrow{AB} \cdot \overrightarrow{AC}$.
- En déduire une mesure de l'angle géométrique $\widehat{BAC}$.
- Calculer les coordonnées du vecteur $\overrightarrow{AD}$.
- Calculer le produit scalaire $\overrightarrow{AB} \cdot \overrightarrow{AD}$.
- Les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AD}$ sont-ils orthogonaux ? Justifier.
Exercice 2
Dans un repère orthonormé de l'espace, on considère les vecteurs $\vec{u}(3, -2, 1)$, $\vec{v}(1, 4, 0)$ et $\vec{w}(-2, -1, 2)$.
- Calculer le produit scalaire $\vec{u} \cdot \vec{v}$.
- Les vecteurs $\vec{u}$ et $\vec{v}$ sont-ils orthogonaux ? Justifier.
- Calculer les normes des vecteurs $\vec{u}$ et $\vec{w}$.
- Calculer le produit scalaire $\vec{u} \cdot \vec{w}$.
- En déduire une mesure de l'angle entre les vecteurs $\vec{u}$ et $\vec{w}$.
- Déterminer la valeur de $k$ pour que le vecteur $\vec{z}(k, 1, 2)$ soit orthogonal à $\vec{u}$.
Exercice 3
Dans un repère orthonormé $(O; \vec{i}, \vec{j}, \vec{k})$, on considère les points $A(1, -1, 2)$, $B(3, 2, 0)$, et $C(0, 1, -2)$.
- Calculer les coordonnées des vecteurs $\overrightarrow{AB}$, $\overrightarrow{AC}$, et $\overrightarrow{BC}$.
- Calculer les normes $||\overrightarrow{AB}||$, $||\overrightarrow{AC}||$, et $||\overrightarrow{BC}||$.
- Calculer les produits scalaires suivants :
- $\overrightarrow{AB} \cdot \overrightarrow{AC}$
- $\overrightarrow{BA} \cdot \overrightarrow{BC}$
- $\overrightarrow{CA} \cdot \overrightarrow{CB}$
- Déterminer une mesure en degrés de l'angle $\widehat{BAC}$.
- Déterminer une mesure en degrés de l'angle $\widehat{ABC}$.
- Déterminer une mesure en degrés de l'angle $\widehat{BCA}$.
Exercice de base 4: Vecteurs colinéaires
Les vecteurs $\vec{u}(1, 2, -1)$ et $\vec{v}(-2, -4, 2)$ sont-ils colinéaires ? Justifier.
Exercice de base 5: Représentation paramétrique d'une droite
Donner une représentation paramétrique de la droite passant par $A(1, 0, -1)$ et de vecteur directeur $\vec{u}(2, -1, 3)$.
Exercice de base 6: Equation cartésienne d'un plan
Donner une équation cartésienne du plan passant par $A(1, 1, 1)$ et de vecteur normal $\vec{n}(2, -1, 1)$.
Exercice de base 7: Vecteur normal à un plan
Le plan a pour équation $3x - 2y + z + 5 = 0$. Donner un vecteur normal à ce plan.
Exercice de base 8: Orthogonalité d'une droite et d'un plan
La droite a pour vecteur directeur $\vec{u}(1, 2, -1)$ et le plan a pour vecteur normal $\vec{n}(2, -1, 1)$. La droite est-elle orthogonale au plan ?
Exercice de base 9: Intersection d'une droite et d'un plan
Déterminer le point d'intersection de la droite $ \begin{cases} x=t\\y=1+t\\z=2-t\end{cases} , t \in \mathbb{R}$ et du plan $x + y + z - 5 = 0$.
Exercice de base 10: Droites parallèles
Les droites $d_1$ de vecteur directeur $\vec{u_1}(1, 2, -1)$ et $d_2$ de vecteur directeur $\vec{u_2}(2, 4, -2)$ sont-elles parallèles ? Justifier.
Exercice de base 11: Plans parallèles
Les plans $P_1$ d'équation $2x - y + 3z - 1 = 0$ et $P_2$ d'équation $-4x + 2y - 6z + 5 = 0$ sont-ils parallèles ? Justifier.
Exercice de base 12: Distance d'un point à un plan
Calculer la distance du point $A(1, 2, 3)$ au plan d'équation $2x - y + 2z - 5 = 0$.
Exercice de base 13: Volume d'un tétraèdre (Hors programme pour aller plus loin...)
Calculer le volume du tétraèdre de sommets $A(0, 0, 0)$, $B(1, 0, 0)$, $C(0, 1, 0)$ et $D(0, 0, 1)$.
Exercice de base 14: Aire d'un triangle dans l'espace (Hors programme pour aller plus loin...)
Calculer l'aire du triangle de sommets $A(1, 0, 0)$, $B(0, 1, 0)$ et $C(0, 0, 1)$.
Exercice de base 15: Projeté orthogonal sur un plan
Déterminer les coordonnées du projeté orthogonal du point $A(1, 2, 3)$ sur le plan $(xOy)$.
Exercice de base 16: Equations de plans parallèles aux axes
Donner une équation du plan parallèle au plan $(xOy)$ et passant par le point $A(2,3,5)$.
Exercice de base 17: Vecteur directeur d'une droite
Donner un vecteur directeur de la droite $ \begin{cases} x=1+2t\\y=-t\\z=3+t\end{cases} , t \in \mathbb{R}$.
Exercice de base 18: Point appartenant à une droite
Le point $A(3, -1, 5)$ appartient-il à la droite $ \begin{cases} x=1+t\\y=2-2t\\z=1+t\end{cases} , t \in \mathbb{R}$ ?
Exercice de base 19: Point appartenant à un plan
Le point $A(2, 1, 1)$ appartient-il au plan d'équation $x - 2y + z - 1 = 0$ ?
Exercice de base 20: Projeté orthogonal sur un axe
Donner les coordonnées du projeté orthogonal du point $A(1, 2, 3)$ sur l'axe $(Oz)$.
Volumes et tétraèdres
Exercice 21: Bac, 20 mars 2023 - Volume d'un tétraèdre dans un cube
On considère le cube ABCDEFGH d'arête 1. On appelle I le point d'intersection du plan (GBD) avec la droite (EC). L'espace est rapporté au repère orthonormé $( A~;~\overrightarrow{AB},~\overrightarrow{AD},~\overrightarrow{AE})$.
- Donner dans ce repère les coordonnées des points E, C, G.
- Déterminer une représentation paramétrique de la droite (EC).
- Démontrer que la droite (EC) est orthogonale au plan (GBD).
-
- Justifier qu'une équation cartésienne du plan (GBD) est : $x + y - z - 1 = 0$.
- Montrer que le point I a pour coordonnées $(\frac23~;~\frac23~;~\frac13)$.
- En déduire que la distance du point E au plan (GBD) est égale à $\frac{2\sqrt 3}{3}$.
-
- Démontrer que le triangle BDG est équilatéral.
- Calculer l'aire du triangle BDG. On pourra utiliser le point J, milieu du segment [BD].
- Justifier que le volume du tétraèdre EGBD est égal à $\frac13$. On rappelle que le volume d'un tétraèdre est donné par $V = \frac13 Bh$ où $B$ est l'aire d'une base du tétraèdre et $h$ est la hauteur relative à cette base.
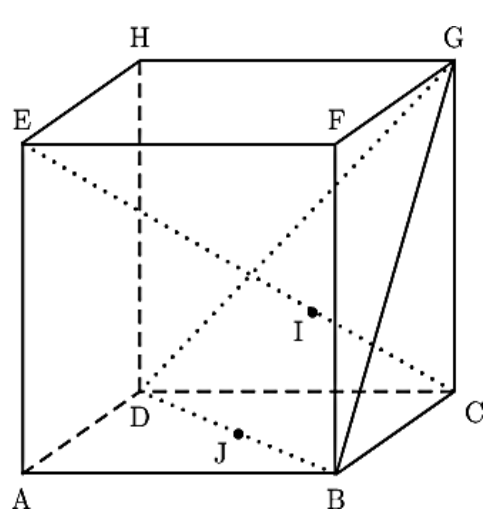
Exercice 22: Bac 2022 - Volume d'un tétraèdre dans un cube
On considère un cube ABCDEFGH et on appelle K le milieu du segment [BC]. On se place dans le repère $( A~;~\overrightarrow{AB},~\overrightarrow{AD},~\overrightarrow{AE})$ et on considère le tétraèdre EFGK. On rappelle que le volume d'un tétraèdre est donné par: $V=\frac13 \times \mathcal{B} \times h$ où $\mathcal{B}$ désigne l'aire d'une base et $h$ la hauteur relative à cette base.
Figure
- Préciser les coordonnées des points E, F, G et K.
- Montrer que le vecteur $\vec{n}\begin{pmatrix}2\\-2\\1\end{pmatrix}$ est orthogonal au plan (EGK).
- Démontrer que le plan (EGK) admet pour équation cartésienne : $2x - 2y + z - 1 = 0$.
- Déterminer une représentation paramétrique de la droite $(d)$ orthogonale au plan (ECK) passant par F.
- Montrer que le projeté orthogonal L de F sur le plan (EGK) a pour coordonnées $(\frac59~;~\frac49~;~\frac79)$.
- Justifier que la longueur LF est égale à $\frac23$.
- Calculer l'aire du triangle EFG. En déduire que le volume du tétraèdre EFGK est égal à $\frac16$.
- Déduire des questions précédentes l'aire du triangle EGK.
- On considère les points P milieu du segment [EG], M milieu du segment [EK] et N milieu du segment[GK]. Déterminer le volume du tétraèdre FPMN.
Représentation paramétrique et orthogonalité
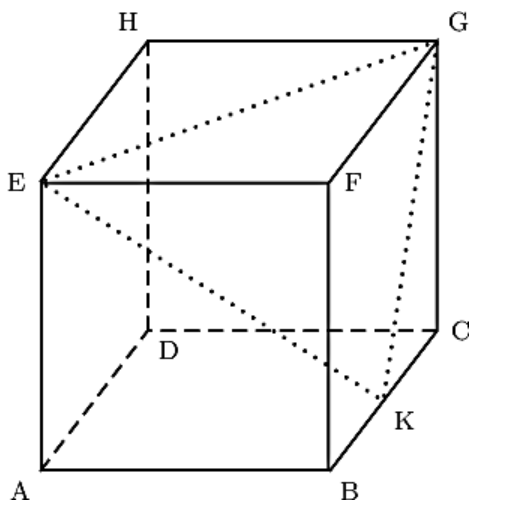
Exercice 23: Bac 2022 - Représentation paramétrique et projeté orthogonal
Dans l'espace rapporté à un repère orthonormé $( O;\vec{i},\vec{j},\vec{k})$, on considère:
Figure
le point A de coordonnées $(-1~;~1~;~3)$,
la droite $\mathcal{D}$ dont une représentation paramétrique est: $ \begin{cases} x=1+2t\\y = 2 - t\\z= 2+2t \end{cases} , t \in \mathbb{R}$.
-
- Donner les coordonnées d'un vecteur directeur $\vec{u}$ de la droite $\mathcal{D}$. On admet que le point A n'appartient pas à la droite $\mathcal{D}$.
- Montrer que le point $B( -1~;~3~;~0)$ appartient à la droite $\mathcal{D}$.
- Calculer le produit scalaire $\overrightarrow{AB} \cdot \vec{u}$.
- On note $\mathcal{P}$ le plan passant par le point A et orthogonal à la droite $\mathcal{D}$, et on appelle H le point d'intersection du plan $\mathcal{P}$ et de la droite $\mathcal{D}$. Ainsi, H est le projeté orthogonal de A sur la droite $\mathcal{D}$.
- Montrer que le plan $\mathcal{P}$ admet pour équation cartésienne: $2x - y + 2z - 3 = 0$.
- En déduire que le point H a pour coordonnées $(\frac79~;~\frac{19}{9}~;~\frac{16}{9})$.
- Calculer la longueur AH. On donnera une valeur exacte.
- Dans cette question, on se propose de retrouver les coordonnées du point H, projeté orthogonal du point A sur la droite $\mathcal{D}$, par une autre méthode. On rappelle que le point B$(-1;3;0)$ appartient à la droite $\mathcal{D}$ et que le vecteur $\vec{u}$ est un vecteur directeur de la droite $\mathcal{D}$.
- Justifier qu'il existe un nombre réel $k$ tel que $\overrightarrow{HB} = k\vec{u}$.
- Montrer que $k = \frac{\overrightarrow{AB} \cdot \vec{u}}{\left\|\vec{u}\right\|^2}$.
- Calculer la valeur du nombre réel $k$ et retrouver les coordonnées du point H.
- On considère un point C appartenant au plan $\mathcal{P}$ tel que le volume du tétraèdre ABCH soit égal à $\frac89$. Calculer l'aire du triangle ACH. On rappelle que le volume d'un tétraèdre est donné par: $V = \frac13 \times \mathcal{B} \times h$ où $\mathcal{B}$ désigne l'aire d'une base et $h$ la hauteur relative à cette base.
Géométrie dans un cube
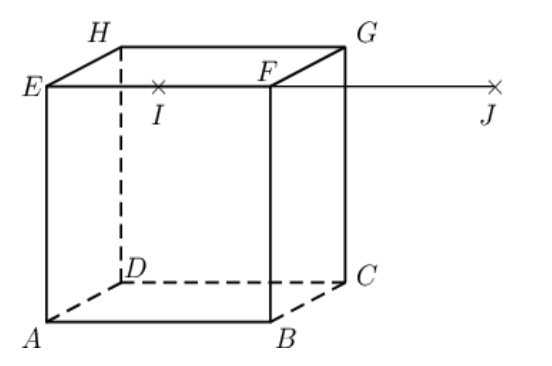
Exercice 24: Bac 2021 - Géométrie dans un cube
On considère le cube ABCDEFGH de côté 1, I est le milieu de [EF] et J le symétrique de E par rapport à F. Dans tous les exercices, l'espace est rapporté au repère orthonormé $( A,\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE})$.
Figure
-
- Par lecture graphique, donner les coordonnées de $I$ et $J$.
- En déduire les coordonnées des vecteurs $\overrightarrow{DJ}$, $\overrightarrow{BI}$ et $\overrightarrow{BG}$.
- Montrer que $\overrightarrow{DJ}$ est un vecteur normal au plan $(BGI)$.
- Montrer qu'une équation cartésienne du plan $(BGI)$ est $2x-y+z-2=0$.
- On note $d$ la droite passant par $F$ et orthogonale au plan $(BGI)$.
- Déterminer une représentation paramétrique de la droite $d$.
- On considère le point $L$ de coordonnées $(\frac23;\frac16;\frac56)$. Montrer que $L$ est le point d'intersection de la droite $d$ et du plan $(BGI)$.
- On rappelle que le volume $V$ d'une pyramide est donné par la formule $V=\frac13 \times \mathcal{B} \times h$, où $\mathcal{B}$ est l'aire d'une base et $h$ la hauteur associée à cette base.
- Calculer le volume de la pyramide $FBGI$.
- En déduire l'aire du triangle $BGI$.
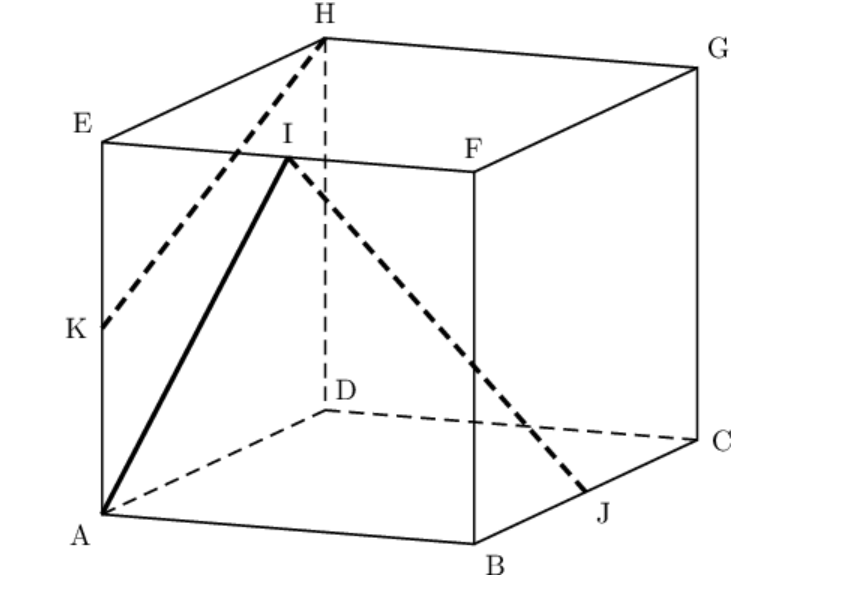
Exercice 25: Bac 2021, Amérique du nord - Géométrie dans un cube et représentation paramétrique de droites
On considère un cube ABCDEFGH. Le point I est le milieu du segment [EF], le point J est le milieu du segment [BC] et le point K est le milieu du segment [AE].
Figure
- Les droites (AI) et (KH) sont-elles parallèles ? Justifier votre réponse.
- Dans la suite, on se place dans le repère orthonormé $( A~;~\overrightarrow{AB},~ \overrightarrow{AD},~ \overrightarrow{AE})$.
- Donner les coordonnées des points I et J.
- Montrer que les vecteurs $\overrightarrow{IJ},~\overrightarrow{AE}$ et $\overrightarrow{AC}$ sont coplanaires.
- On considère le plan $\mathcal P$ d'équation $x + 3y - 2z + 2 = 0$ ainsi que les droites $d_1$ et $d_2$ définies par les représentations paramétriques ci-dessous:
$d_1 : \begin{cases} x=3 + t\\ y = 8 - 2t\\ z= - 2 + 3t\\ \end{cases} , t \in \mathbb{R}$ et $d_2 : \begin{cases} x=4 + t\\ y = 1 + t\\ z= 8 + 2t\\ \end{cases} , t \in \mathbb{R}$.- Les droites $d_1$ et $d_2$ sont-elles parallèles ? Justifier votre réponse.
- Montrer que la droite $d_2$ est parallèle au plan $\mathcal P$.
- Montrer que le point $L(4~;~0~;~3)$ est le projeté orthogonal du point $M(5~;~3~;~1)$ sur le plan $\mathcal P$.
QCM de géométrie dans l'espace
Exercice 26: Bac 2021 - QCM de géométrie dans l'espace
Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées
est exacte.
Une réponse exacte rapporte un point. Une réponse fausse, une réponse multiple
ou l'absence de réponse à une question ne rapporte ni n'enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre
de la réponse choisie.
Aucune justification n'est demandée.
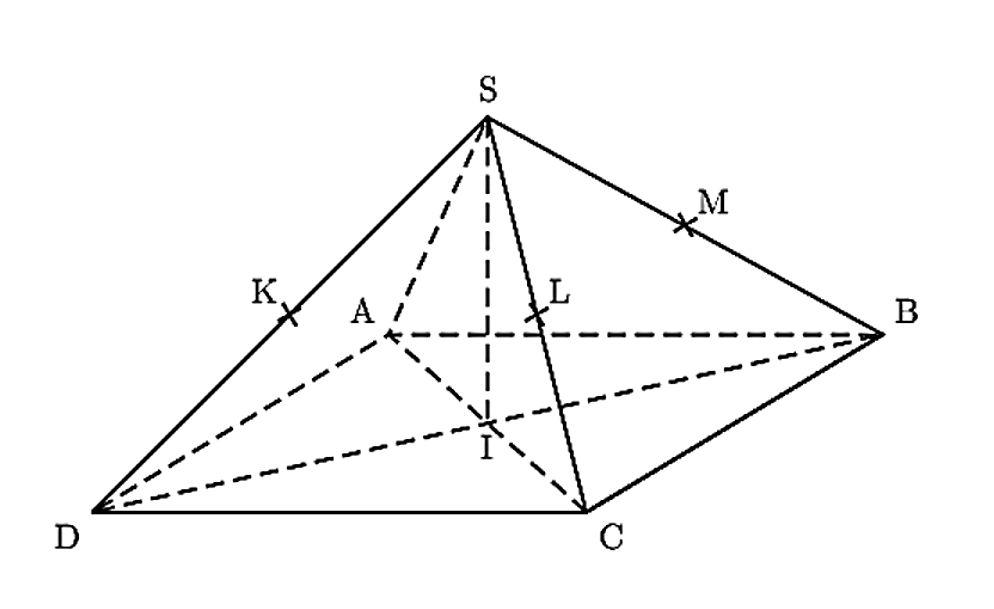
Pyramide régulière SABCD
SABCD est une pyramide régulière à base carrée ABCD dont toutes les arêtes ont la même longueur.
Le point I est le centre du carré ABCD. On suppose que: IC = IB = IS = 1.
Les points K, L et M sont les milieux respectifs des arêtes [SD], [SC] et [SB].
- Les droites suivantes ne sont pas coplanaires:
a. (DK) et (SD)
b. (AS) et (IC)
c. (AC) et (SB)
d. (LM) et (AD) - Pour les questions suivantes, on se place dans le repère orthonormé
de l'espace $( I~;~ \overrightarrow{IC},~\overrightarrow{IB},~\overrightarrow{IS})$. Dans ce repère, on donne les coordonnées des points suivants:
$I(0;0;0) ; A(-1;0;0) ; B(0;1;0) ; C(1;0;0) ; D(0;-1;0) ; S(0;0;1)$
Les coordonnées du milieu N de [KL] sont:
a. $(\frac{1}{4}~;~\frac{1}{4}~;~\frac{1}{4})$
b.$(\frac{1}{4}~;~- \frac{1}{4}~;~\frac{1}{2})$
c.$(-\frac{1}{4}~;~\frac{1}{4}~;~\frac{1}{2})$
d.$(-\frac{1}{2}~;~\frac{1}{2}~;~1)$ - Les coordonnées du vecteur $\overrightarrow{AS}$ sont:
a. $\begin{pmatrix}1\\1\\0 \end{pmatrix}$
b. $\begin{pmatrix}1\\0\\1 \end{pmatrix}$
c. $\begin{pmatrix}2\\1\\-1 \end{pmatrix}$
d. $\begin{pmatrix} 1\\1\\1\end{pmatrix}$ - Une représentation paramétrique de la droite (AS) est:
a. $\begin{cases}x=-1-t\\y=t\\z=-t\end{cases} , (t \in \mathbb{R})$
b. $\begin{cases}x=-1+2t\\y=0\\z=1 + 2t\end{cases} (t \in \mathbb{R})$
c. $\begin{cases}x=t\\y=0\\z=1+t\end{cases}(t \in \mathbb{R})$
d. $\begin{cases}x=-1-t\\y=1+t\\z=1-t\end{cases}(t \in \mathbb{R})$ - Une équation cartésienne du plan (SCB) est:
a. $y+z-1 =0$
b.$x+y+z- 1=0$
c.$x-y+z=0$
d.$x+z-1 =0$
Distance point à un plan et volume d'une pyramide
Exercice 27: Bac 2021 - Distance point à un plan et volume d'une pyramide
Dans l'espace rapporté à un repère orthonormé $( O, \vec{i}, \vec{j}, \vec{k})$, on considère les points: A de coordonnées (2;0;0), B de coordonnées (0;3;0) et C de coordonnées (0;0;1).
L'objectif de cet exercice est de calculer l'aire du triangle ABC.
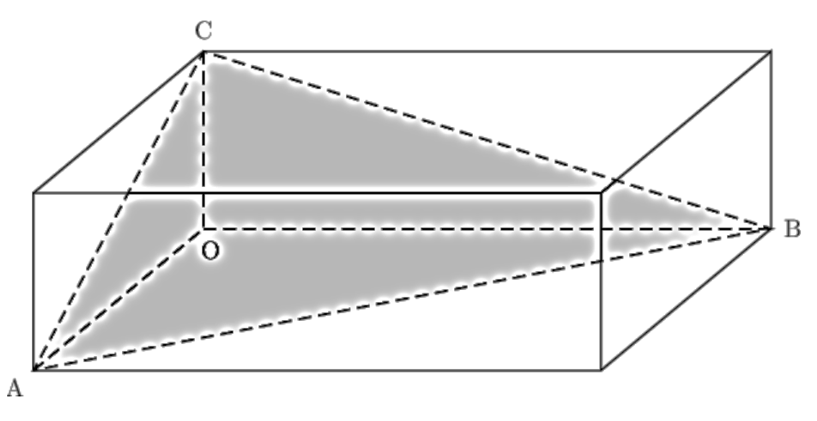
Figure
-
- Montrer que le vecteur $\vec{n}\begin{pmatrix}3\\2\\6\end{pmatrix}$ est normal au plan (ABC).
- En déduire qu'une équation cartésienne du plan (ABC) est : $3x + 2y + 6z - 6 = 0$.
- On note $d$ la droite passant par O et orthogonale au plan (ABC).
- Déterminer une représentation paramétrique de la droite $d$.
- Montrer que la droite $d$ coupe le plan (ABC) au point H de coordonnées $(\frac{18}{49}~;~\frac{12}{49}~;~\frac{36}{49})$.
- Calculer la distance OH.
- On rappelle que le volume d'une pyramide est donné par: $V = \frac{1}{3}\mathcal{B}h$, où $\mathcal{B}$ est l'aire d'une base et $h$ est la hauteur de la pyramide correspondant à cette base. En calculant de deux façons différentes le volume de la pyramide OABC, déterminer l'aire du triangle ABC.
Orthogonalité, projection et minimisation de distance
Exercice 28: Bac 2021 - Orthogonalité dans l'espace et minimisation d'une distance et volume d'une pyramide
Dans un repère orthonormé $( O;\vec{i},\vec{j},\vec{k})$ on considère
le point A de coordonnées (1;3;2),
le vecteur $\vec{u}$ de coordonnées $\begin{pmatrix} 1\\1\\0\\\end{pmatrix}$
la droite $d$ passant par l'origine O du repère et admettant pour vecteur directeur $\vec{u}$.
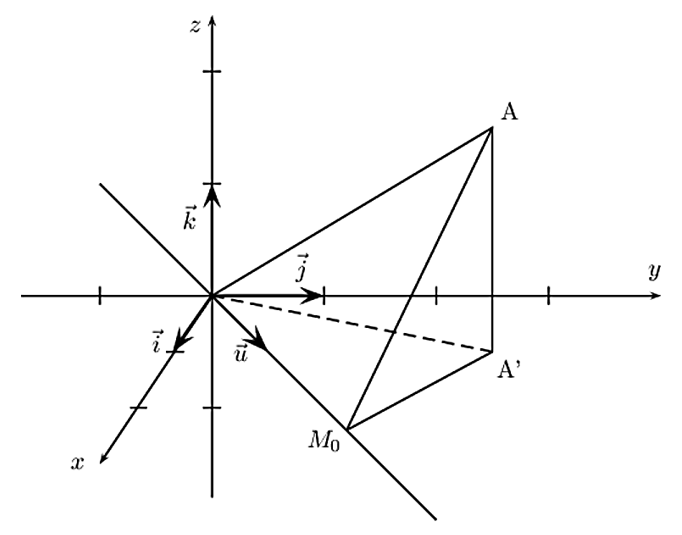
Figure
Le but de cet exercice est de déterminer le point de $d$ le plus proche du point A et d'étudier quelques propriétés de ce point.
- Déterminer une représentation paramétrique de la droite $d$.
- Soit $t$ un nombre réel quelconque, et $M$ un point de la droite $d$, le point $M$ ayant pour coordonnées $(t~;~t~;~0)$.
- On note AM la distance entre les points A et M. Démontrer que: $AM^2 = 2t^2 - 8t+ 14$.
- Démontrer que le point $M_0$ de coordonnées $(2~;~2~;~0)$ est le point de la droite $d$ pour lequel la distance $AM$ est minimale. On admettra que la distance $AM$ est minimale lorsque son carré $AM^2$ est minimal.
- Démontrer que les droites $(AM_0)$ et $d$ sont orthogonales.
- On appelle $A'$ le projeté orthogonal du point $A$ sur le plan d'équation cartésienne $z = 0$. Le point $A'$ admet donc pour coordonnées $(1~;~3~;~0)$. Démontrer que le point $M_0$ est le point du plan $(AA'M_0)$ le plus proche du point O, origine du repère.
- Calculer le volume de la pyramide $OM_0A'A$. On rappelle que le volume d'une pyramide est donné par: $V = \frac{1}{3}\mathcal{B}h$, où $\mathcal{B}$ est l'aire d'une base et $h$ est la hauteur de la pyramide correspondant à cette base.
Droites et plans, intersection
Exercice 29: Bac 2018, Pondichéry - Droite, plan, intersection
Dans l'espace muni du repère orthonormé $( O; \vec{i}, \vec{j}, \vec{k})$ d'unité 1 cm, on considère les points A, B, C et D de coordonnées respectives (2;1;4), (4;-1;0), (0;3;2) et (4;3;-2).
- Déterminer une représentation paramétrique de la droite (CD).
- Soit M un point de la droite (CD).
- Déterminer les coordonnées du point M tel que la distance BM soit minimale.
- On note H le point de la droite (CD) ayant pour coordonnées (3;3;-1). Vérifier que les droites (BH) et (CD) sont perpendiculaires.
- Montrer que l'aire du triangle BCD est égale à $12\,\text{cm}^2$.
-
- Démontrer que le vecteur $\vec{n}\begin{pmatrix}2\\1\\2\end{pmatrix}$ est un vecteur normal au plan (BCD).
- Déterminer une équation cartésienne du plan (BCD).
- Déterminer une représentation paramétrique de la droite $\Delta$ passant par A et orthogonale au plan (BCD).
- Démontrer que le point I, intersection de la droite $\Delta$ et du plan (BCD) a pour coordonnées $(\frac{2}{3}~;~\frac{1}{3}~;~\frac{8}{3})$.
- Calculer le volume du tétraèdre ABCD.
Droites perpendiculaires dans l'espace
Exercice 30: Bac 2015, Nouvelle Calédonie - Droites perpendiculaires dans l'espace
L'espace est rapporté au repère orthonormé $( O;\vec{i},\vec{j},\vec{k})$. On désigne par $\mathbb{R}$ l'ensemble des nombres réels.
On rappelle que deux droites de l'espace sont dites perpendiculaires si et seulement si elles sont orthogonales et sécantes.
Soient le point $A_1$ de coordonnées $(0~;~2~;~-1)$ et le vecteur
$\overrightarrow{u_1}$ de coordonnées $\begin{pmatrix}1\\2\\3\end{pmatrix}$.
On appelle $D_1$ la droite passant par $A_1$ et de vecteur directeur
$\overrightarrow{u_1}$.
On appelle $D_2$ la droite qui admet pour représentation paramétrique
$\begin{cases}
x=1 + k\\y= - 2k\\ z=2\end{cases}, k \in \mathbb{R}$.
Le but de l'exercice est de prouver l'existence d'une droite perpendiculaire à la fois à $D_1$ et $D_2$.
-
- Donner une représentation paramétrique de $D_1$.
- Donner un vecteur directeur de $D_2$ (on le notera : $\overrightarrow{u_2}$).
- Le point $A_2(- 1~;~4~;~2)$ appartient-il à $D_2$ ?
- Démontrer que les droites $D_1$ et $D_2$ sont non coplanaires.
- Soit le vecteur $\vec{v}\begin{pmatrix}- 6\\- 3\\4\end{pmatrix}$. On définit la droite $\Delta_1$ passant par $A_1$ et de vecteur directeur $\vec{v}$ et la droite $\Delta_2$ passant
par $A_2$ et parallèle à $\Delta_1$. Justifier que les droites $D_1$ et $\Delta_1$ sont perpendiculaires.
Dans la suite, on admettra que les droites $D_2$ et $\Delta_2$ sont perpendiculaires.
- Soit $P_1$ le plan défini par les droites $D_1$ et $\Delta_1$ et
$P_2$ le plan défini par les droites $D_2$ et $\Delta_2$.
- Soit le vecteur $\vec{n}\begin{pmatrix}17\\- 22\\9\end{pmatrix}$. Vérifier que $\vec{n}$ est un vecteur normal au plan $P_1$.
- Montrer que $P_1$ et $P_2$ ne sont pas parallèles.
- Soit $\Delta$ la droite d'intersection des plans $P_1$ et $P_2$. On admettra que le vecteur $\vec{v}$ est un vecteur directeur de $\Delta$. Utiliser les questions précédentes pour prouver qu'il existe une droite de l'espace perpendiculaire à la fois à $D_1$ et à $D_2$.
Géométrie dans l'espace
Exercice 31: Bac 2015 - Géométrie dans l'espace
Dans un repère orthonormé (O, I, J, K) d'unité 1 cm, on considère les points
$A(0;-1;5)$, $B(2;-1;5)$, $C(11;0;1)$, $D(11;4;4)$.
Un point $M$ se déplace sur la droite $(AB)$ dans le sens de $A$ vers $B$ à la vitesse de 1cm par seconde.
Un point $N$ se déplace sur la droite $(CD)$ dans le sens de $C$ vers $D$ à la vitesse de 1cm par seconde.
À l'instant $t=0$ le point $M$ est en $A$ et le point $N$ est en $C$.
On note $M_t$ et $N_t$ les positions des points $M$ et $N$ au bout de $t$ secondes, $t$ désignant un nombre réel positif.
On admet que $M_t$ et $N_t$, ont pour coordonnées : $M_t(t;-1;5)$ et $N_t(11;0,8t;1+0,6t)$.
Les questions 1 et 2 sont indépendantes.
-
- La droite $(AB)$ est parallèle à l'un des axes $(OI)$, $(OJ)$ ou $(OK)$. Lequel ?
- La droite $(CD)$ se trouve dans un plan $\mathcal{P}$ parallèle à l'un des plans $(OIJ)$, $(OIK)$ ou $(OJK)$. Lequel ? On donnera une équation de ce plan $\mathcal{P}$.
- Vérifier que la droite $(AB)$, orthogonale au plan $\mathcal{P}$, coupe ce plan au point $E(11;-1;5)$.
- Les droites $(AB)$ et $(CD)$ sont-elles sécantes ?
-
- Montrer que $M_tN_t^2 = 2 t^2 - 25,2 t + 138$.
- À quel instant $t$ la longueur $M_tN_t$ est-elle minimale?
Géométrie dans un tétraèdre
Exercice 32: Bac 2014 - Géométrie dans l'espace, dans un tétraèdre…
Dans l'espace, on considère un tétraèdre $ABCD$ dont les faces $ABC$,
$ACD$ et $ABD$ sont des triangles rectangles et isocèles en A.
On désigne par $E$, $F$ et $G$ les milieux respectifs des côtés
$[AB]$, $[BC]$ et $[CA]$.
On choisit $AB$ pour unité de longueur et on se place dans le repère
orthonormé $( A;\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD})$ de l'espace.
-
On désigne par $\mathcal{P}$ le plan qui passe par A et qui est orthogonal à la droite (DF).
On note H le point d'intersection du plan $\mathcal{P}$ et de la droite (DF).
- Donner les coordonnées des points D et F.
- Donner une représentation paramétrique de la droite (DF).
- Déterminer une équation cartésienne du plan $\mathcal{P}$.
- Calculer les coordonnées du point H.
- Démontrer que l'angle $\widehat{\text{EHG}}$ est un angle droit.
-
On désigne par $M$ un point de la droite $(DF)$ et par $t$ le réel tel que $\overrightarrow{DM} = t\overrightarrow{DF}$.
On note $\alpha$ la mesure en radians de l'angle géométrique $\widehat{EMG}$.
Le but de cette question est de déterminer la position du point $M$ pour que $\alpha$ soit maximale.
- Démontrer que $ME^2 = \frac{3}{2}t^2-\frac{5}{2}t+\frac{5}{4}$.
- Démontrer que le triangle $MEG$ est isocèle en $M$. En déduire que $ME\sin (\frac{\alpha}{2})=\frac{1}{2\sqrt{2}}$.
- Justifier que $\alpha$ est maximale si et seulement si $\sin (\frac{\alpha}{2} )$ est maximal. En déduire que $\alpha$ est maximale si et seulement si $ME^2$ est minimal.
- Conclure.