Thème : Convexité
Exercice 1
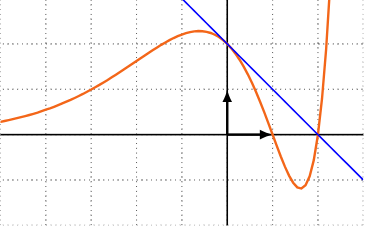
On considère la fonction dérivable \(f\) dont la courbe représentative est donnée ci-dessous. On a également tracé la tangente à cette courbe au point d'abscisse 0.
Figure
1. Déterminer graphiquement \(f'(0)\).
2. Donner une équation réduite de la tangente à la courbe de \(f\) au point d'abscisse 0.
3. Déterminer graphiquement le signe de \(f'(-3)\).
4. La fonction \(f\) semble-t-elle convexe ou concave sur \([-5\, ;\, -2]\) ? sur \([-2\,;\,1]\) ? sur \([1 \, ; 2\,]\) ?
Exercice 2
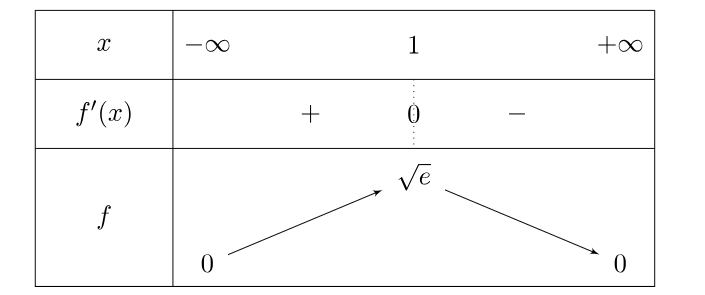
On considère une fonction \(f\) dont le tableau de variations est donné ci-dessous.
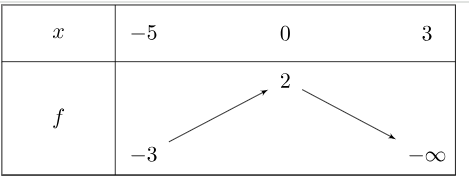
Tableau de variations
On sait de plus que \(f\) est convexe sur \([-5;-2]\) puis concave sur \([-2;3]\). Tracer une courbe représentative compatible avec ces données.
Exercice 3
L'objectif de cet exercice est de démontrer que la fonction \(x\mapsto x^2\) est convexe sur \(\mathbb{R}\). Le plan est muni d'un repère orthonormé \((O, \vec i, \vec j)\). On note \(\mathcal{C}\) la courbe de la fonction \(f:x\mapsto x^2\) dans ce repère.
1. Cas particulier : On considère les points \(A\) et \(B\) de coordonnées respectives \((-2;4)\) et \((3;9)\).
a. Justifier que ces points appartiennent bien à la courbe \(\mathcal{C}\).
b. Vérifier que l'équation réduite de la droite \((AB)\) est \(y=x+6\).
c. Étudier le signe de \(x^2-(x+6)\) sur l'intervalle \([-2;3]\) et conclure.
2. Cas général : Soit \(a\) et \(b\) deux réels avec \(a a. Montrer que l'équation réduite de la droite \((AB)\) est \(y=(a+b)x-ab\). b. Étudier le signe de \(x^2-((a+b)x-ab)\) sur \([a;b]\) et conclure.
Exercice 4
On considère la fonction \(f:x\mapsto \dfrac{1}{x}\), définie et dérivable sur \(]0;+\infty[\). Soit \(a\) un réel strictement positif.
1. Montrer que pour tout réel strictement positif \(x\), \(f(x)-(f'(a)(x-a)+f(a))=\dfrac{(a-x)^2}{a^2x}\).
2. La fonction \(f\) est-elle convexe ou concave sur \(]0;+\infty[\) ?
Exercice 5
Soit \(a\) et \(b\) deux réels. Montrer que la fonction \(x\mapsto e^{ax+b}\), définie et deux fois dérivable sur \(\mathbb{R}\), est également convexe sur \(\mathbb{R}\).
Exercice 6
Montrer que la fonction \(\ln\) est concave sur \(]0;+\infty[\).
Exercice 7
On donne ci-dessous, dans le plan rapporté à un repère orthonormé, la courbe représentant la fonction dérivée \(f’\) d’une fonction \(f\) dérivable sur \(\mathbb{R}\).
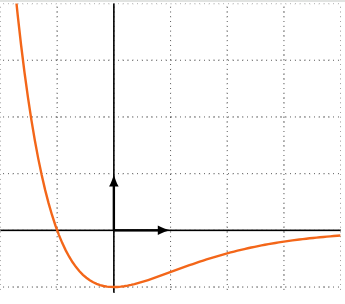
Tableau de signe de $f'$
1. Le sens de variations de la fonction \(f\) sur \(\mathbb{R}\)
2. La convexité de la fonction \(f\) sur \(\mathbb{R}\)
Exercice 8
Pour tout réel \(x\), on pose \(f(x)=3x^3+3x^2-4x+1\).
1. Pour tout réel \(x\), déterminer \(f^{\prime\prime}(x)\).
2. En déduire les intervalles sur lesquels \(f\) est convexe.
3. La courbe représentative de la fonction \(f\) possède-t-elle un point d’inflexion ? Si oui, en quelle abscisse ?
Exercice 9
Pour tout réel \(x\), on pose \(f(x)=x^4+2x^2-3x+1\). La fonction \(f\) admet-elle un point d’inflexion ?
Exercice 10
On considère la fonction \(f:x\mapsto \ln(1+x^2)\).
1. Justifier que \(f\) est définie et dérivable sur \(\mathbb{R}\) et calculer \(f'(x)\).
2. Construire le tableau de variations de \(f\) en y incluant les limites.
3. Résoudre l’équation \(f(x)=1\) sur \(\mathbb{R}\).
4. Justifier que \(f\) est deux fois dérivable sur \(\mathbb{R}\) et que pour tout réel \(x\), \(f^{\prime\prime}(x)= \dfrac{2-2x^2}{(1+x^2)^2}\).
5. Construire le tableau de signes de \(f^{\prime\prime}\) et en déduire les intervalles lesquels \(f\) est convexe/concave.
6. Donner les équations des tangentes à la courbe de \(f\) aux points d’abscisses 1 et \(-1\).
7. Dans un repère orthonormé, tracer la courbe représentative de \(f\) ainsi que ses tangentes aux points d’abscisse 1 et \(-1\).