Revoyons ensemble les points essentiels sur les Vecteurs et Translations avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Vecteurs : Définition et Caractéristiques
Définition : Un vecteur est un objet mathématique défini par :
Une direction : donnée par la droite qui le porte.
Un sens : un sens de parcours sur cette droite (de l'origine vers l'extrémité).
Une norme (ou longueur) : la distance entre l'origine et l'extrémité.
Représentant : Un vecteur peut être représenté par une infinité de segments orientés (flèches) appelés représentants. Un représentant est défini par une origine et une extrémité.
Notation : Un vecteur est noté avec une flèche au-dessus, par exemple $\vec{u}$, ou par deux points désignant son origine et son extrémité, par exemple $\overrightarrow{AB}$.
Vecteurs égaux : Deux vecteurs sont égaux s'ils ont la même direction, le même sens et la même norme. En termes de représentants, cela signifie que le quadrilatère formé par leurs origines et extrémités est un parallélogramme (éventuellement aplati).
2. Opérations sur les Vecteurs
Somme vectorielle : La somme de deux vecteurs $\vec{u}$ et $\vec{v}$ se construit graphiquement par la règle du parallélogramme ou la relation de Chasles.
Relation de Chasles : Pour tous points $A$, $B$ et $C$, on a $\overrightarrow{AB}$ + $\overrightarrow{BC}$ = $\overrightarrow{AC}$. Cette relation est fondamentale pour simplifier des expressions vectorielles.
Règle du parallélogramme : Si $OAEB$ est un parallélogramme, alors $\overrightarrow{OA}$ + $\overrightarrow{OB}$ = $\overrightarrow{OE}$.
Multiplication par un scalaire : Multiplier un vecteur $\vec{u}$ par un nombre réel $k$ (scalaire) donne un nouveau vecteur $k\vec{u}$ qui a :
même direction que $\vec{u}$.
même sens que $\vec{u}$ si $k > 0$, sens opposé si $k < 0$.
norme multipliée par $|k|$ : $\|k\vec{u}\| = |k| \times \|\vec{u}\|$.
3. Vecteurs et Repérage Cartésien
Coordonnées d'un vecteur : Dans un repère $(O, \vec{i}, \vec{j})$, un vecteur $\vec{u}$ peut être défini par ses coordonnées $\begin{pmatrix} x \\ y \end{pmatrix}$, où $x$ est la composante horizontale et $y$ la composante verticale.
Coordonnées du vecteur $\overrightarrow{AB}$ : Si $A(x_A, y_A)$ et $B(x_B, y_B)$, alors $\overrightarrow{AB} = \begin{pmatrix} x_B - x_A \\ y_B - y_A \end{pmatrix}$.
Opérations sur les coordonnées :
Somme de vecteurs : Si $\vec{u} \begin{pmatrix} x \\ y \end{pmatrix}$ et $\vec{v} \begin{pmatrix} x' \\ y' \end{pmatrix}$, alors $\vec{u} + \vec{v} = \begin{pmatrix} x + x' \\ y + y' \end{pmatrix}$.
Multiplication par un scalaire : Si $\vec{u} \begin{pmatrix} x \\ y \end{pmatrix}$ et $k$ est un réel, alors $k\vec{u} = \begin{pmatrix} kx \\ ky \end{pmatrix}$.
Colinéarité : Deux vecteurs $\vec{u} \begin{pmatrix} x \\ y \end{pmatrix}$ et $\vec{v} \begin{pmatrix} x' \\ y' \end{pmatrix}$ sont colinéaires si et seulement si leur déterminant est nul, c'est-à-dire $xy' - x'y = 0$.
4. Translations et Points Définis Vectoriellement
Définition d'une translation : La translation de vecteur $\vec{u}$ est la transformation géométrique qui associe à tout point $M$ un point $M'$ tel que $\overrightarrow{MM'} = \vec{u}$.
Image et antécédent : $M'$ est l'image de $M$ par la translation de vecteur $\vec{u}$, et $M$ est l'antécédent de $M'$ par la même translation.
Points définis vectoriellement : Souvent, les positions de points sont définies par des égalités vectorielles impliquant des sommes et des multiplications par des scalaires. Pour trouver les coordonnées de ces points, on utilise les opérations sur les coordonnées des vecteurs.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Vecteurs et traductions
Exercice 1 : Représentation de vecteurs sur quadrillage
Choisissez $A$, $B$, $C$ et $D$ des points distincts et non alignés du plan sur le quadrillage de votre feuille. Notons $\vec u$ un vecteur dont $\overrightarrow{AB}$ est un représentant.
- Dessinez le représentant $\overrightarrow{AB}$ de $\vec u$.
- Dessinez le représentant de $\vec{u}$ d'origine $C$.
- Dessinez le représentant de $\vec{u}$ d'extrémité $D$.
Exercice 2 : Représentation de vecteurs hors quadrillage
Recommencez l'exercice précédent en présentant maintenant les points hors le quadrillage et en utilisant règle et compas.
Choisissez $A$, $B$, $C$ et $D$ des points distincts et non alignés sur votre feuille (sans quadrillage).- Dessinez le représentant $\overrightarrow{AB}$ de $\vec u$.
- Dessinez le représentant de $\vec{u}$ d'origine $C$ en utilisant règle et compas.
- Dessinez le représentant de $\vec{u}$ d'extrémité $D$ en utilisant règle et compas.
Exercice 3 : Vecteurs égaux et identification
En vous référant à la figure ci-dessous, répondez aux questions suivantes :
- Citez tous les vecteurs égaux au vecteur $\overrightarrow{AE}$ et au vecteur $\overrightarrow{CF}$.
- Citez un vecteur de même direction que $\overrightarrow{CB}$ mais de sens opposé. Faites de même pour $\overrightarrow{AF}$.
- Citez un vecteur égal à $\overrightarrow{DC}$ d'extrémité $F$. Citez un vecteur égal à $\overrightarrow{FB}$ d'origine $A$.
- Citez deux vecteurs de même direction, de même sens qui ne sont pas égaux.
- Citez deux vecteurs de même norme qui ne sont pas égaux.
Exercice 4 : Démonstration avec l'égalité de vecteurs
$RSTU$ est un parallélogramme. $E$ est le point tel que $\overrightarrow{RE} = \overrightarrow{US}$. $F$ est le point tel que $\overrightarrow{TF} = \overrightarrow{RU}$. Démontrer que $RSET$ est un parallélogramme.
Exercice 5 : Construction de somme de vecteurs
Choisissez $4$ points $A$, $B$, $C$ et $D$ non alignés et hors du quadrillage. Construisez un représentant du vecteur somme $\overrightarrow{AB}+\overrightarrow{CD}$.
Exercice 6 : Construction de somme de vecteurs sur quadrillage
Recommencez l'exercice précédent en exploitant les points du quadrillage et en utilisant celui-ci pour répondre à la question.
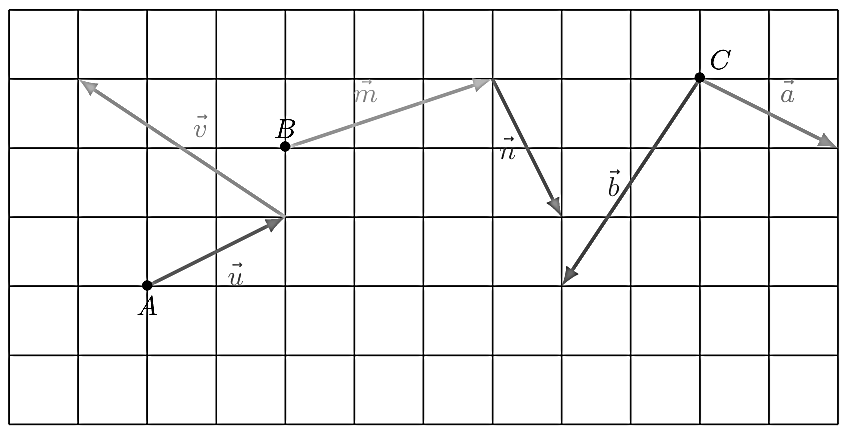
Exercice 7 : Construction de sommes graphiques
Reproduisez la figure ci-dessous et construisez :
- le représentant d'origine $A$ du vecteur $\vec{u}+ \vec{v}$
- le représentant d'origine $B$ du vecteur $\vec{m}+ \vec{n}$
- le représentant d'origine $C$ du vecteur $\vec{a}+ \vec{b}$

Exercice 8 : Simplification d'expressions vectorielles
Soient $A$, $B$, $C$, $E$, $G$ et $I$ des points du plan. Simplifiez les expressions vectorielles suivantes (grâce notamment à la relation de Chasles).
- $\overrightarrow{GE}+\overrightarrow{CG}$
- $\overrightarrow{GE}-\overrightarrow{IE}+\overrightarrow{CG}$
- $\overrightarrow{AB}+\overrightarrow{GE}-\overrightarrow{CB}+\overrightarrow{EI}+\overrightarrow{CG}$
Exercice 9 : Simplifications vectorielles avec relation de Chasles
Simplifiez les expressions vectorielles suivantes :
- $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}$
- $\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BC}-\overrightarrow{BA}$
- $\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{AB}$
Exercice 10 : Démonstrations vectorielles
Démontrez les égalités vectorielles suivantes :
- $\overrightarrow{AB}-\overrightarrow{CD}-\overrightarrow{AC}=\overrightarrow{DB}$
- $\overrightarrow{AB}-\overrightarrow{DB}+\overrightarrow{DE}=\overrightarrow{AE}$
- $\overrightarrow{BE}+\overrightarrow{CB}-\overrightarrow{DE}=\overrightarrow{CD}$
- $\overrightarrow{BD}-\overrightarrow{CA}+\overrightarrow{CB}-\overrightarrow{AD}=\vec 0$
- $\overrightarrow{CB}-\overrightarrow{CA}+\overrightarrow{BD}=\overrightarrow{AD}$
- $\overrightarrow{AC}+\overrightarrow{BD}+\overrightarrow{CE}+\overrightarrow{DA}+\overrightarrow{EB}=\vec 0$