Revoyons ensemble les points essentiels sur les Inéquations Produits et Quotients avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Inéquations produit et quotient
Inéquation produit : Une inéquation produit est de la forme $P(x) \times Q(x) > 0$, $P(x) \times Q(x) < 0$, $P(x) \times Q(x) \geq 0$ ou $P(x) \times Q(x) \leq 0$, où $P(x)$ et $Q(x)$ sont des expressions dépendant de $x$.
Inéquation quotient : Une inéquation quotient est de la forme $\frac{P(x)}{Q(x)} > 0$, $\frac{P(x)}{Q(x)} < 0$, $\frac{P(x)}{Q(x)} \geq 0$ ou $\frac{P(x)}{Q(x)} \leq 0$. Il faut faire attention aux valeurs interdites qui annulent le dénominateur $Q(x)$.
Tableau de signes : La méthode de résolution principale pour ces inéquations est le tableau de signes. Il permet de déterminer le signe du produit ou du quotient en fonction des signes de chaque facteur.
2. Étapes de résolution avec tableau de signes
1. Factorisation : Factoriser si possible le numérateur et le dénominateur en facteurs du premier degré (de la forme $ax+b$) ou des carrés.
2. Valeurs charnières : Trouver les valeurs de $x$ qui annulent chaque facteur (numérateur et dénominateur). Ces valeurs sont les racines des facteurs et les valeurs interdites pour le quotient.
3. Tableau de signes : Construire un tableau avec :
- Une ligne pour les valeurs de $x$ (incluant les valeurs charnières et les valeurs interdites).
- Une ligne pour le signe de chaque facteur.
- Une ligne pour le signe du produit ou quotient (déduit par la règle des signes).
4. Conclusion : Déterminer l'ensemble des solutions en lisant le tableau de signes et en tenant compte du sens de l'inéquation (>, <, $\geq$, $\leq$) et des valeurs interdites.
3. Cas particuliers et astuces
Facteur carré : Un facteur au carré, comme $(x-a)^2$, est toujours positif ou nul. Il ne change pas le signe de l'expression sauf en $x=a$ où il s'annule.
Facteur constant : Un facteur constant (nombre) influence le signe global. Un facteur négatif inverse le signe de l'expression.
Valeurs absolues : Un facteur en valeur absolue, comme $|x-a|$, est toujours positif ou nul. Il ne change pas le signe de l'expression sauf en $x=a$ où il s'annule.
Identités remarquables et factorisation : Utiliser les identités remarquables pour factoriser les expressions du second degré et simplifier la construction du tableau de signes.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Inéquations Produits et Quotients (Seconde)
Exercice 1 : Inéquation produit simple
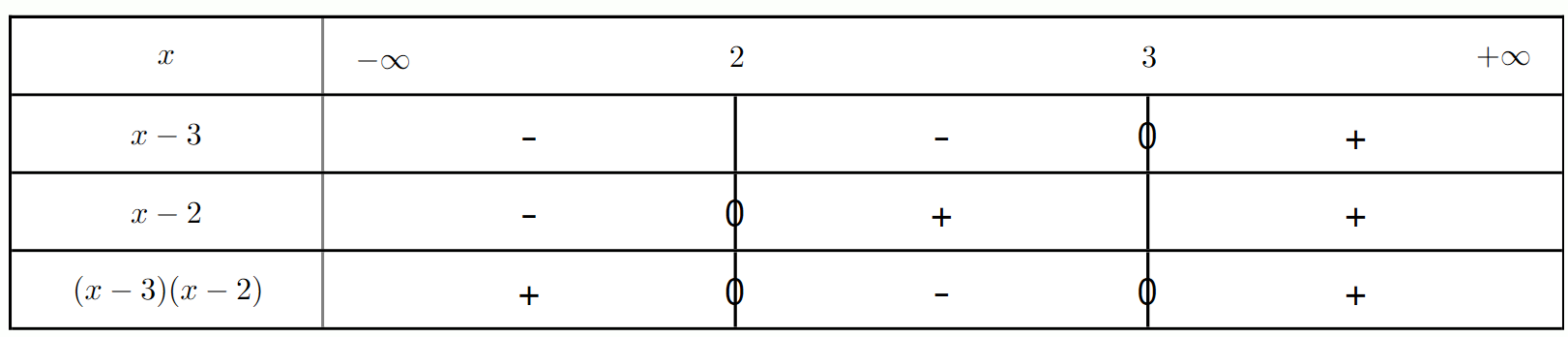
On considère l'inéquation $(x - 3)(x + 2) > 0$.
a) Quelles sont les valeurs de $x$ qui annulent chaque facteur ?
b) Établir le tableau de signes de chaque facteur et du produit.
c) En déduire l'ensemble des solutions de l'inéquation.
d) Comment vérifier graphiquement la solution ?
Exercice 2 : Inéquation quotient simple
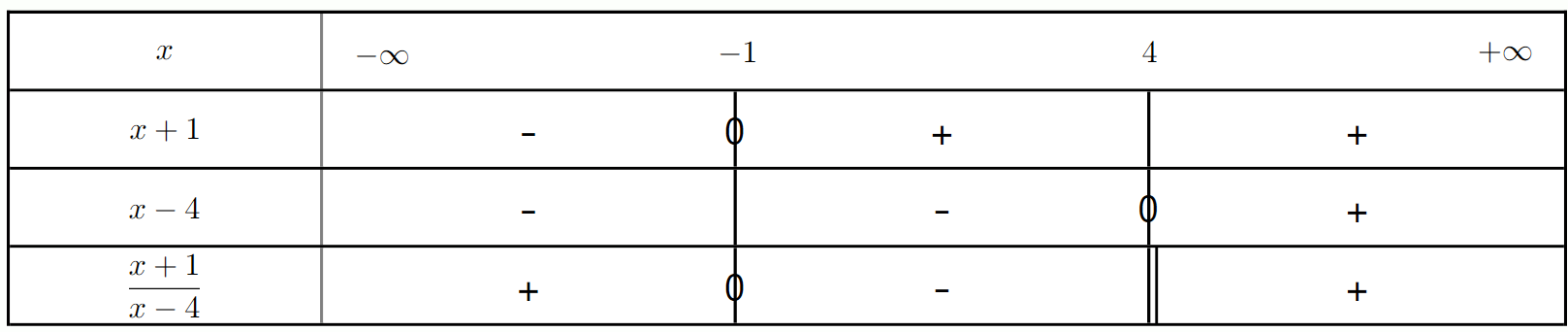
Résoudre l'inéquation $\frac{x + 1}{x - 4} \leq 0$.
a) Quelles sont les valeurs de $x$ qui annulent le numérateur et le dénominateur ?
b) Quelle est la valeur interdite ? Pourquoi ?
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment interpréter la solution en termes de position relative de deux fonctions ?
Exercice 3 : Inéquation produit avec un carré
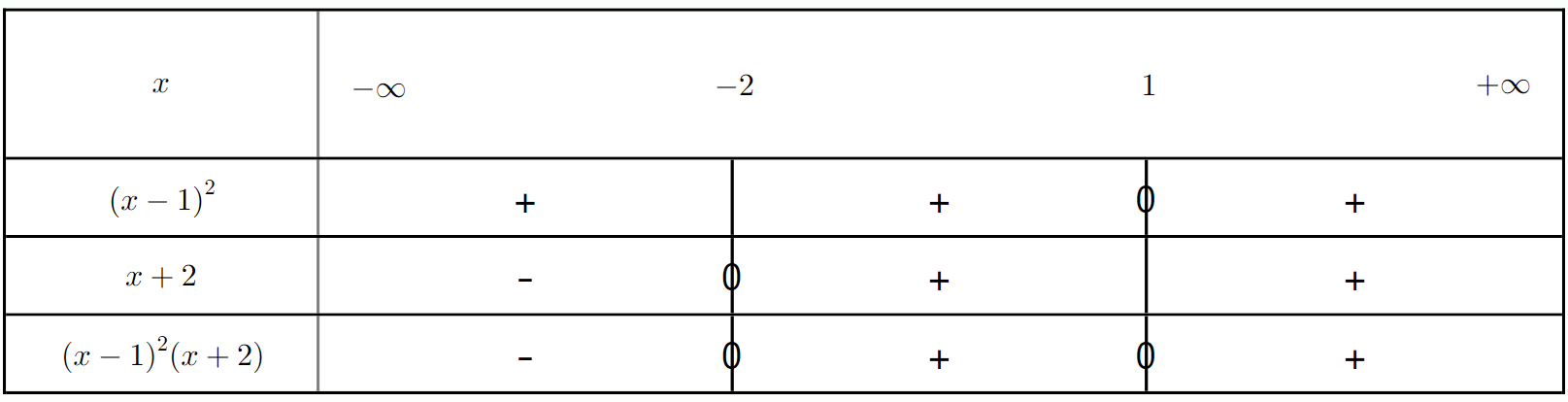
Résoudre l'inéquation $(x - 1)^2(x + 2) \geq 0$.
a) Quelle est la particularité du facteur $(x - 1)^2$ ?
b) Déterminer les valeurs qui annulent chaque facteur.
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment représenter l'ensemble des solutions sur une droite numérique ?
Exercice 4 : Inéquation quotient avec un carré
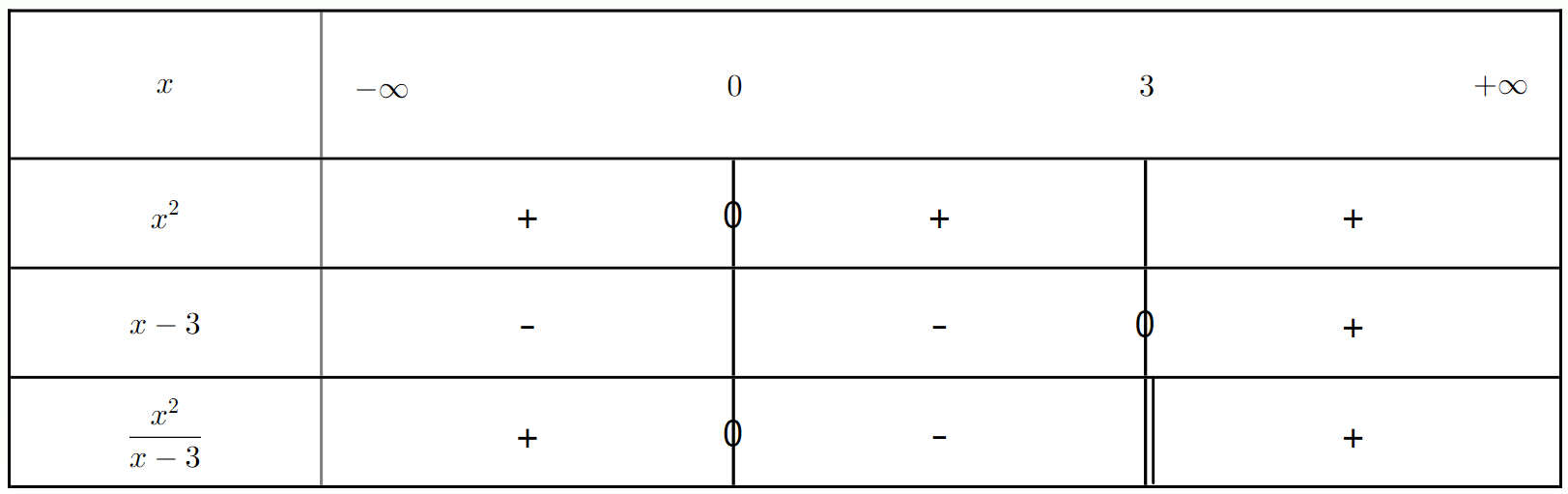
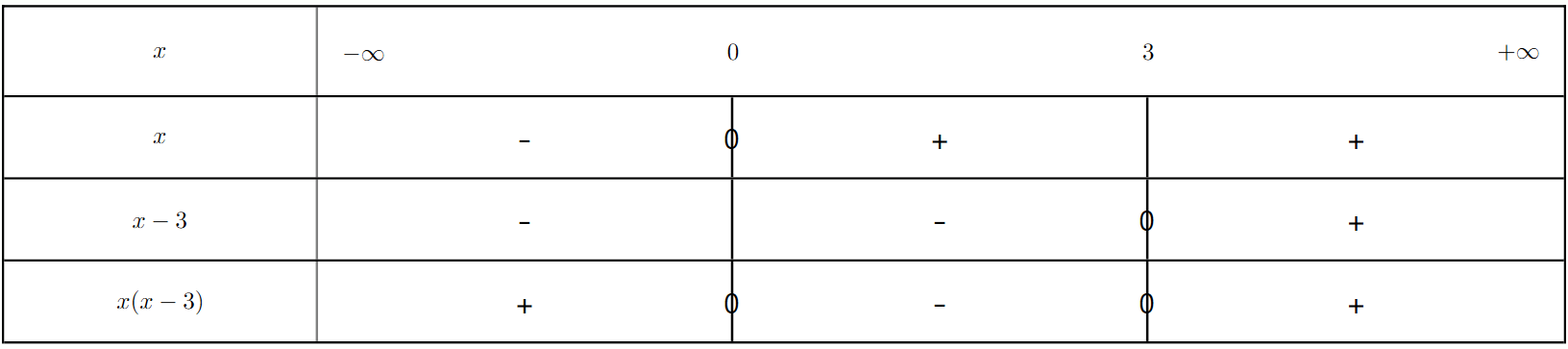
Résoudre l'inéquation $\frac{x^2}{x - 3} > 0$.
a) Quelle est la particularité du facteur $x^2$ ?
b) Déterminer les valeurs qui annulent le numérateur et le dénominateur.
c) Quelle est la valeur interdite ?
d) Établir le tableau de signes et en déduire l'ensemble des solutions.
e) Comment la valeur $x=0$ influence-t-elle la solution ?
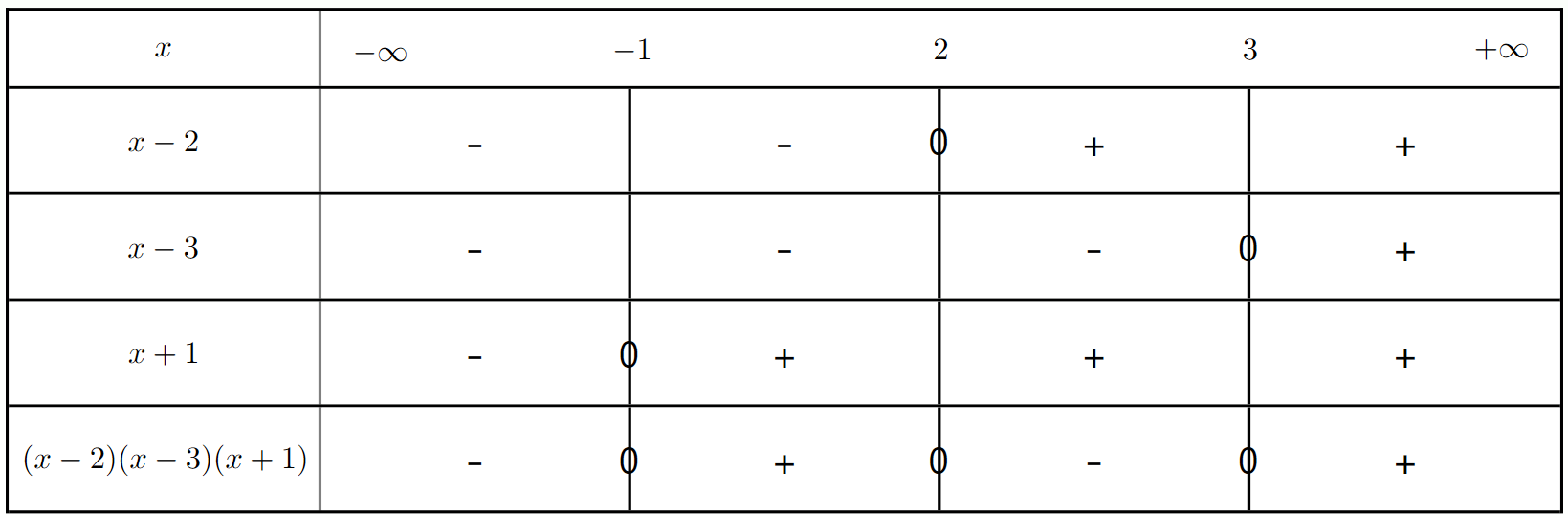
Exercice 5 : Inéquation produit avec trois facteurs
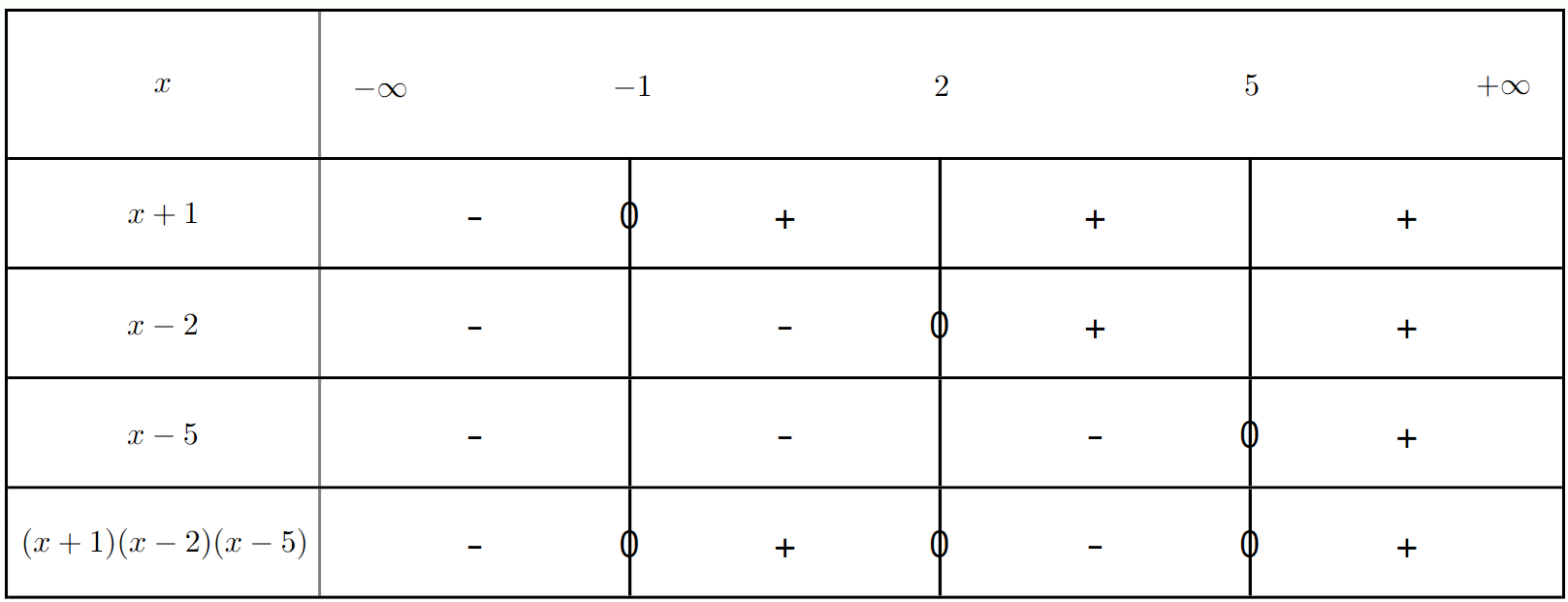
Résoudre l'inéquation $(x + 1)(x - 2)(x - 5) < 0$.
a) Déterminer les valeurs qui annulent chaque facteur.
b) Établir le tableau de signes et en déduire l'ensemble des solutions.
c) Comment vérifier la solution en utilisant un grapheur ?
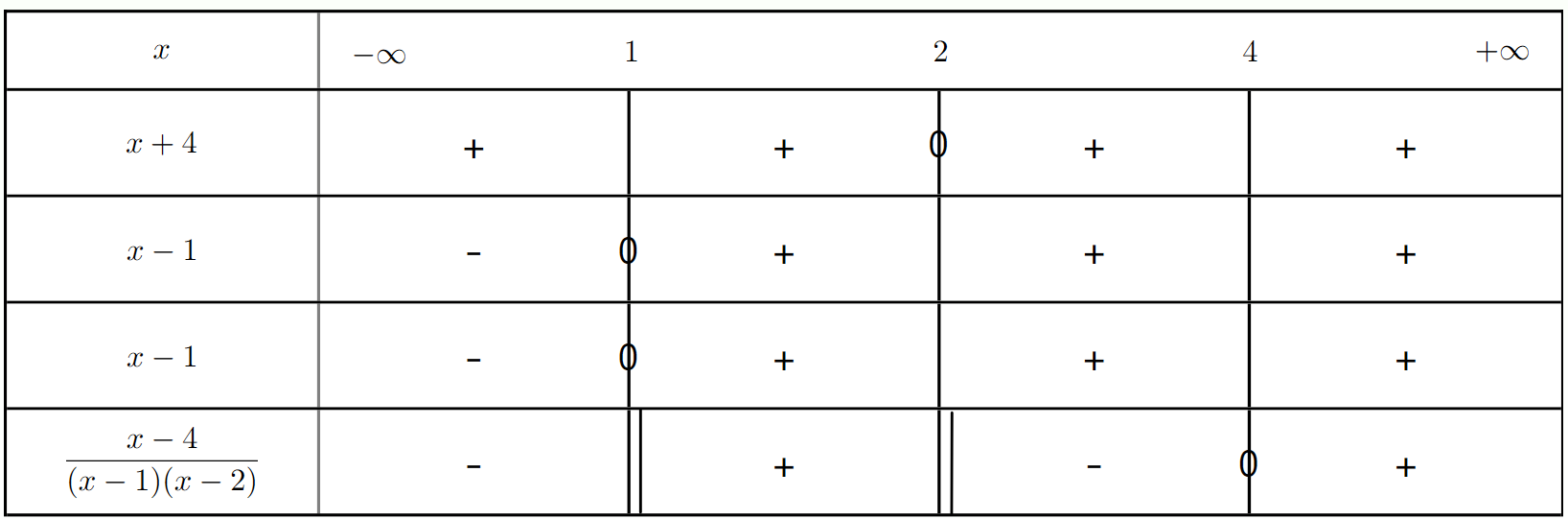
Exercice 6 : Inéquation quotient avec trois facteurs
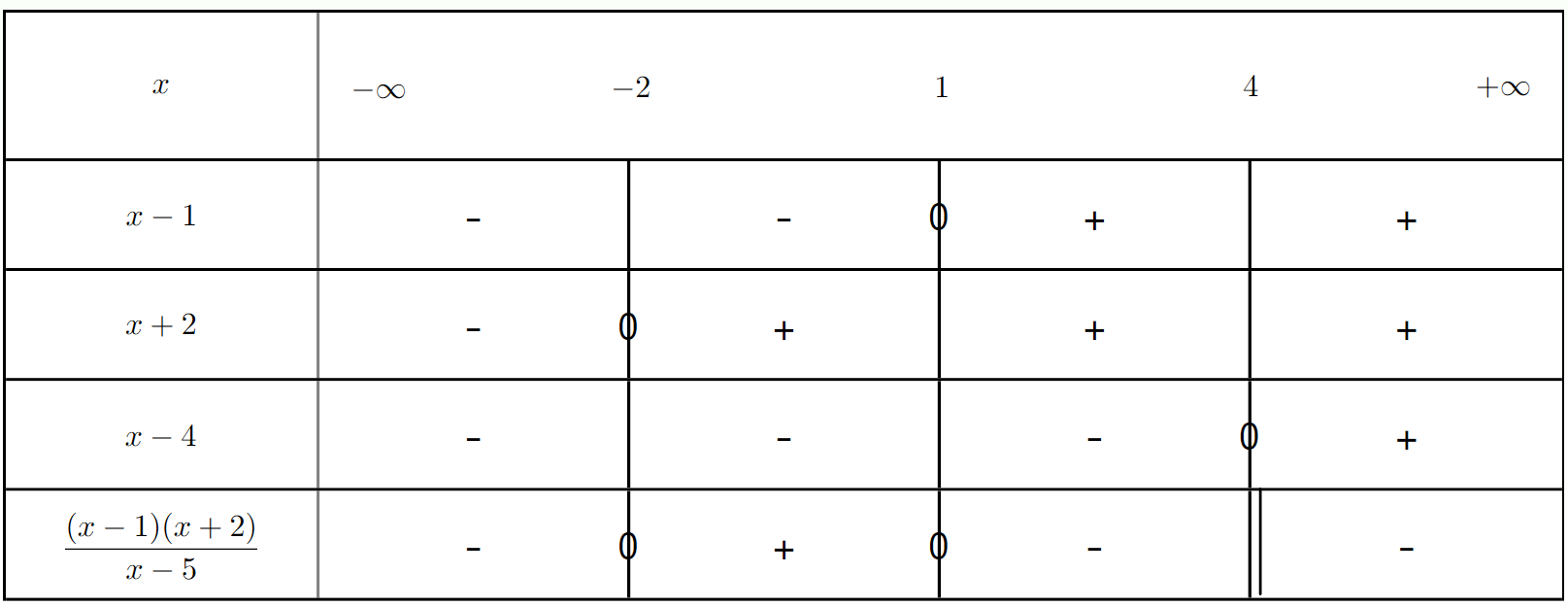
Résoudre l'inéquation $\frac{(x - 1)(x + 2)}{x - 4} \geq 0$.
a) Déterminer les valeurs qui annulent chaque facteur.
b) Identifier la ou les valeurs interdites.
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment interpréter le rôle de la valeur interdite dans la solution ?
Exercice 7 : Inéquation produit avec facteur constant
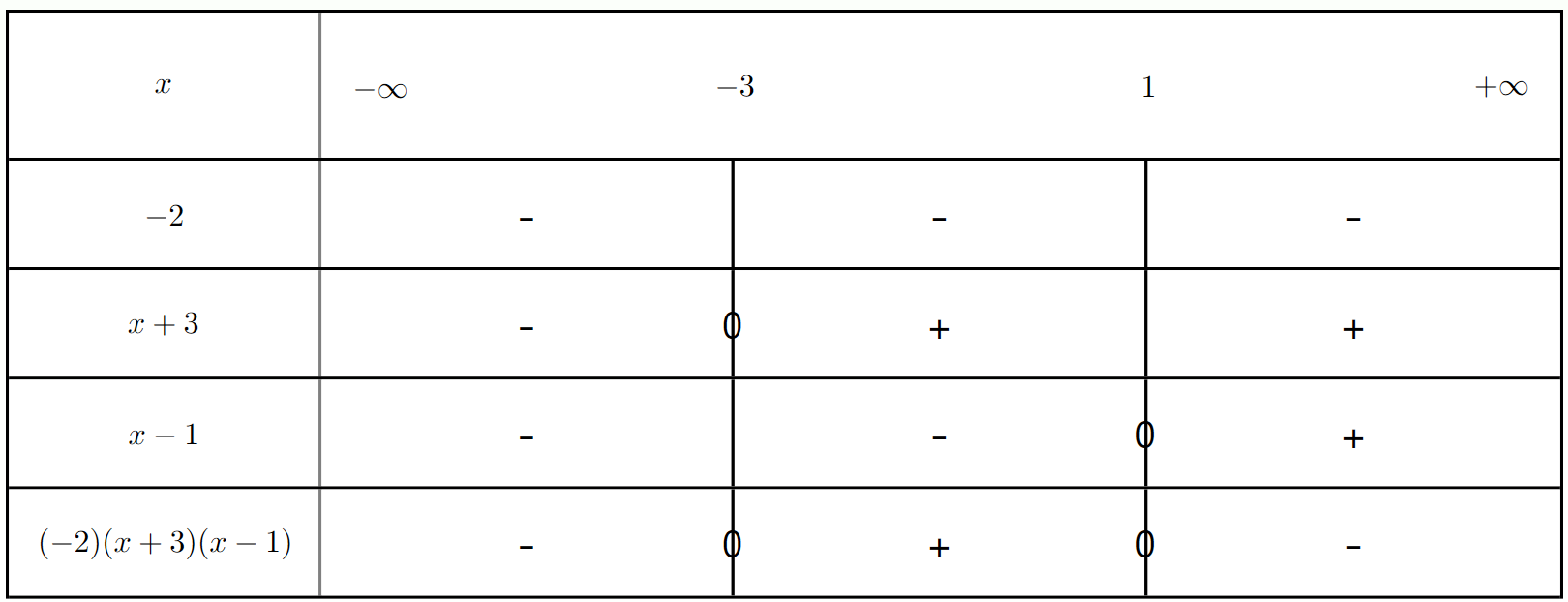
Résoudre l'inéquation $-2(x + 3)(x - 1) \leq 0$.
a) Quel est l'impact du facteur constant -2 sur le signe du produit ?
b) Déterminer les valeurs qui annulent les facteurs variables.
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment le facteur constant influence-t-il le tableau de signes ?
Exercice 8 : Inéquation quotient avec facteur constant
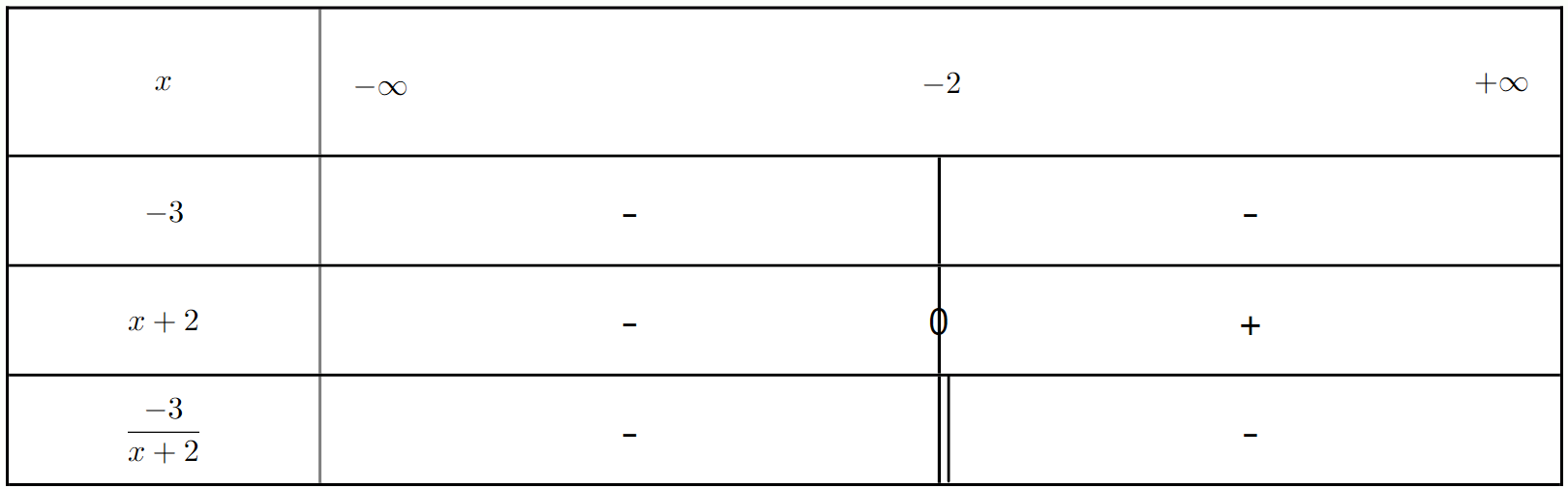
Résoudre l'inéquation $\frac{-3}{x + 2} < 0$.
a) Quel est l'impact du facteur constant -3 sur le signe du quotient ?
b) Déterminer la valeur qui annule le dénominateur et préciser la valeur interdite.
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment résoudre l'inéquation si le numérateur était positif ?
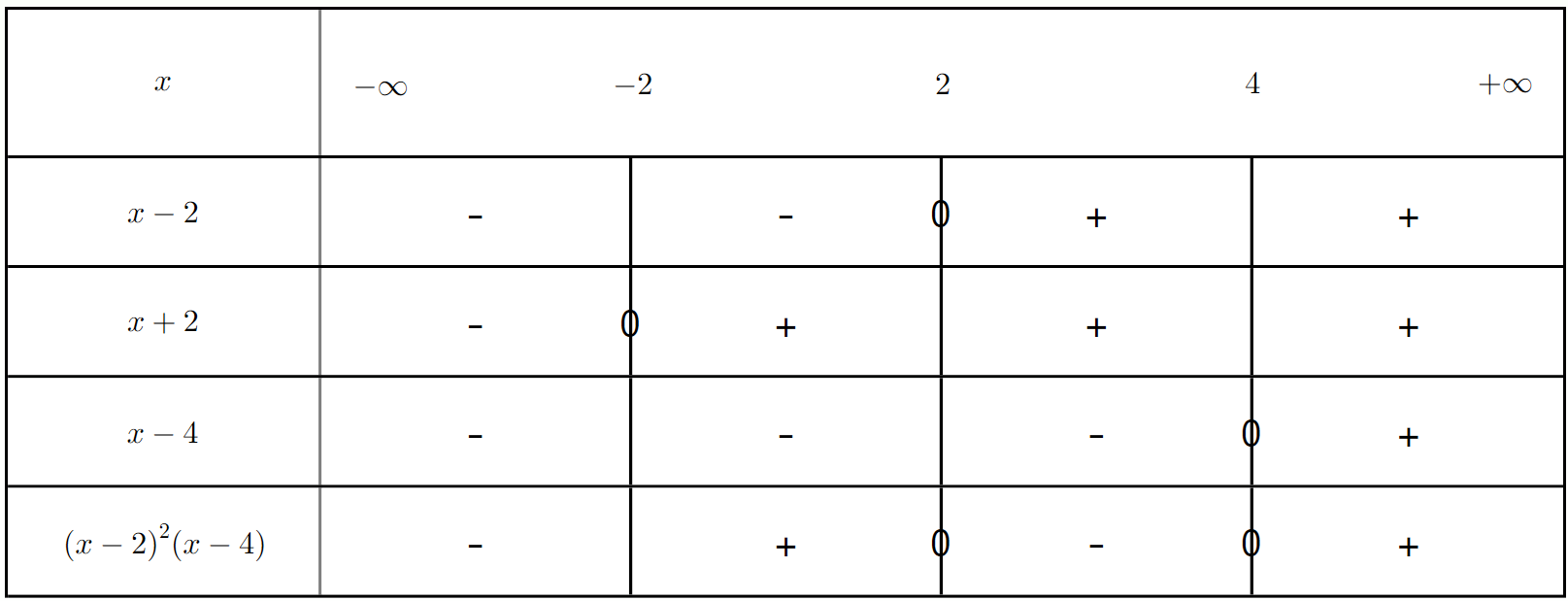
Exercice 9 : Inéquation produit avec identité remarquable
Résoudre l'inéquation $(x^2 - 4)(x + 1) > 0$.
a) Factoriser $x^2 - 4$.
b) Déterminer les valeurs qui annulent chaque facteur.
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Pourquoi est-il crucial de factoriser avant de résoudre l'inéquation ?
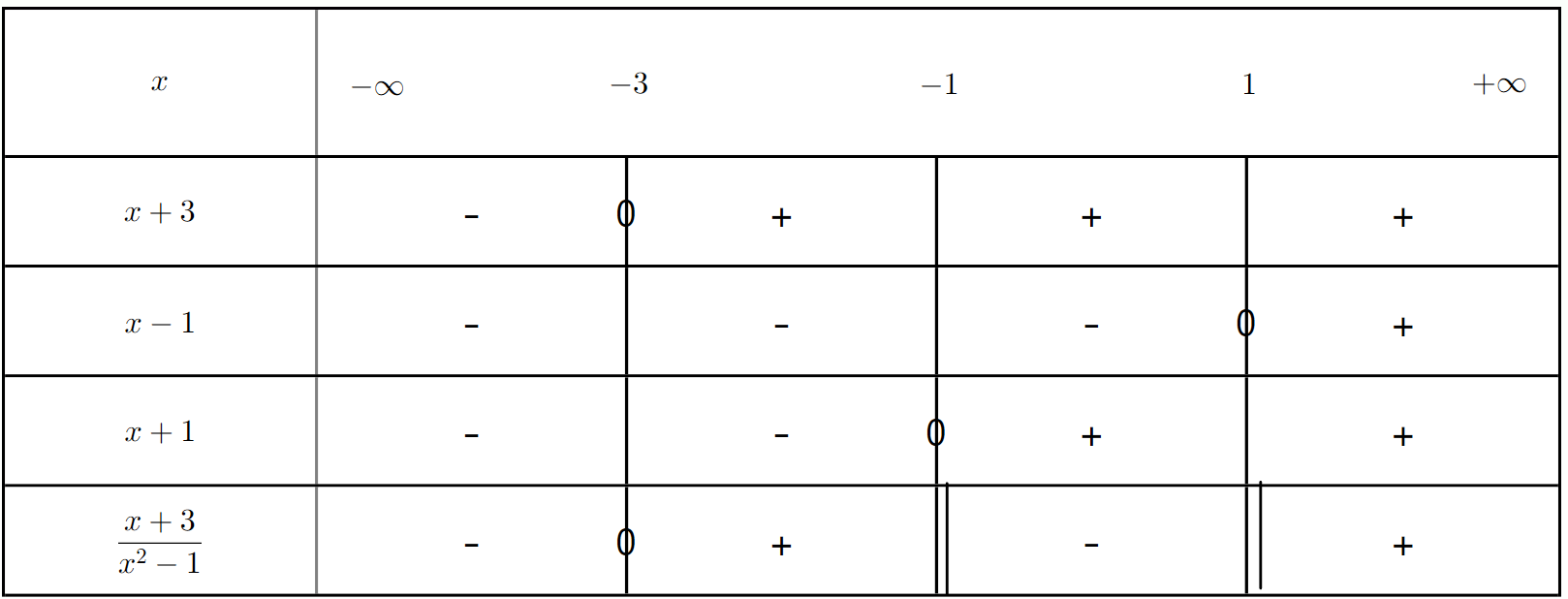
Exercice 10 : Inéquation quotient avec identité remarquable
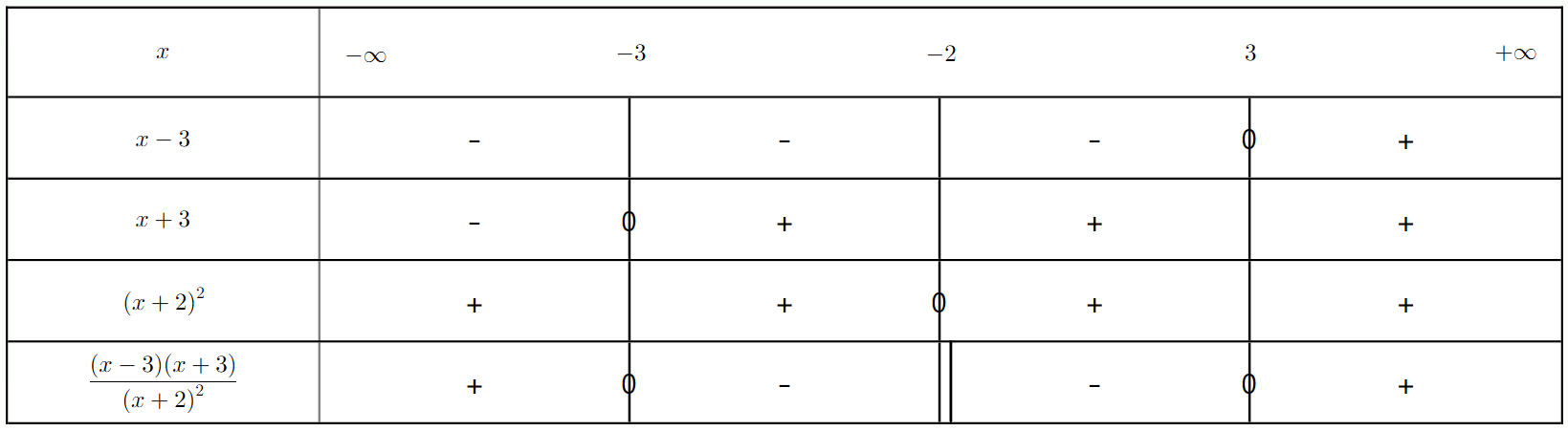
Résoudre l'inéquation $\frac{x + 3}{x^2 - 1} \leq 0$.
a) Factoriser $x^2 - 1$.
b) Déterminer les valeurs qui annulent chaque facteur.
c) Identifier les valeurs interdites.
d) Établir le tableau de signes et en déduire l'ensemble des solutions.
e) Comment les valeurs interdites influencent-elles l'ensemble des solutions ?
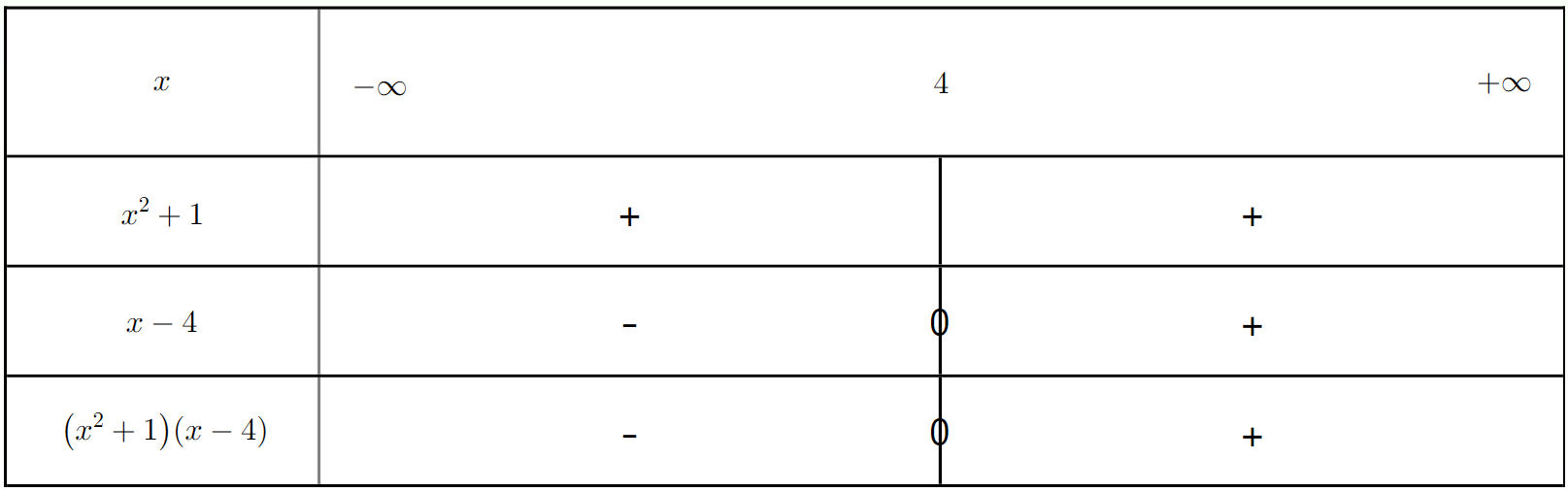
Exercice 11 : Inéquation produit avec un facteur toujours positif
Résoudre l'inéquation $(x^2 + 1)(x - 4) > 0$.
a) Justifier pourquoi $x^2 + 1$ est toujours positif.
b) Déterminer la valeur qui annule le second facteur.
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment simplifier la résolution de l'inéquation en tenant compte du facteur toujours positif ?
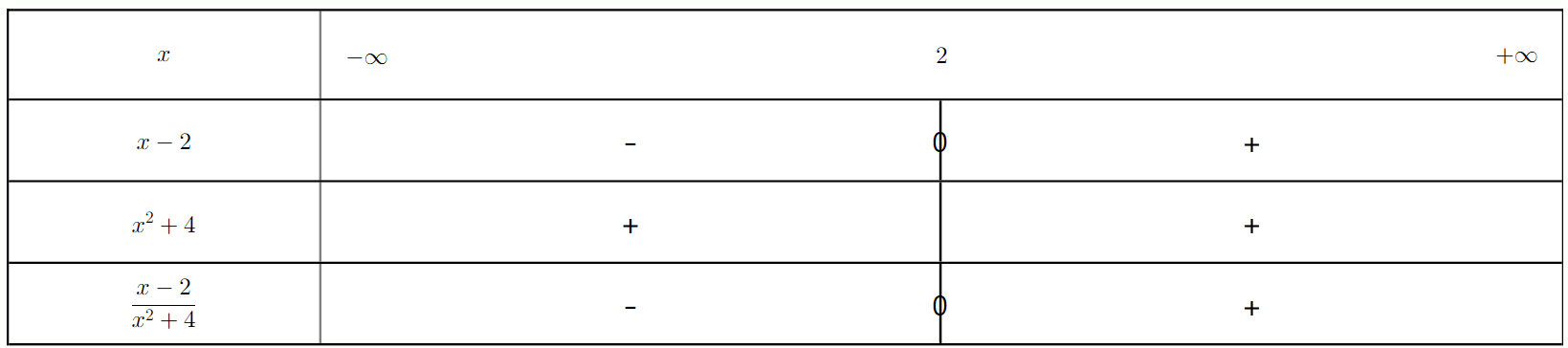
Exercice 12 : Inéquation quotient avec un facteur toujours positif
Résoudre l'inéquation $\frac{x-2}{x^2+4} \le 0$
a) Justifier pourquoi $x^2+4$ est toujours positif.
b) Déterminer la valeur qui annule le numérateur.
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment l'absence de valeurs interdites affecte-t-elle la forme de la solution ?
Exercice 13 : Inéquation produit avec une double racine
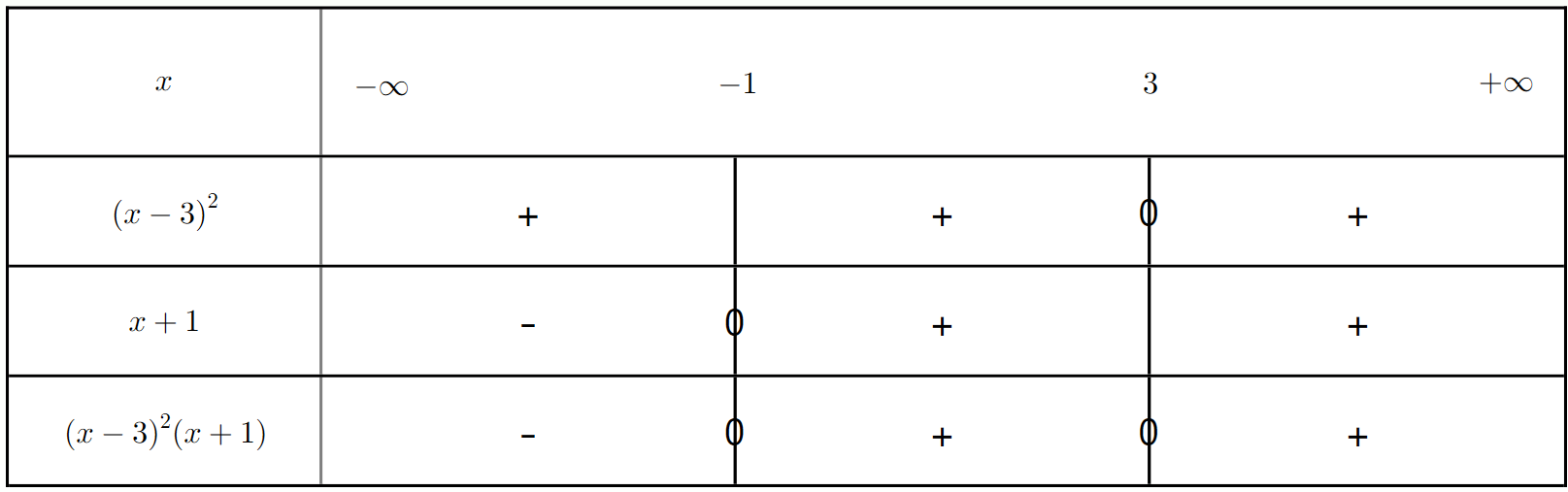
Résoudre l'inéquation $(x-3)^2(x+1) \le 0$
a) Déterminer les valeurs qui annulent chaque facteur.
b) Quel est le signe de $(x-3)^2$ ?
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment la double racine influence-t-elle l'ensemble des solutions ?
Exercice 14 : Inéquation quotient avec une double racine
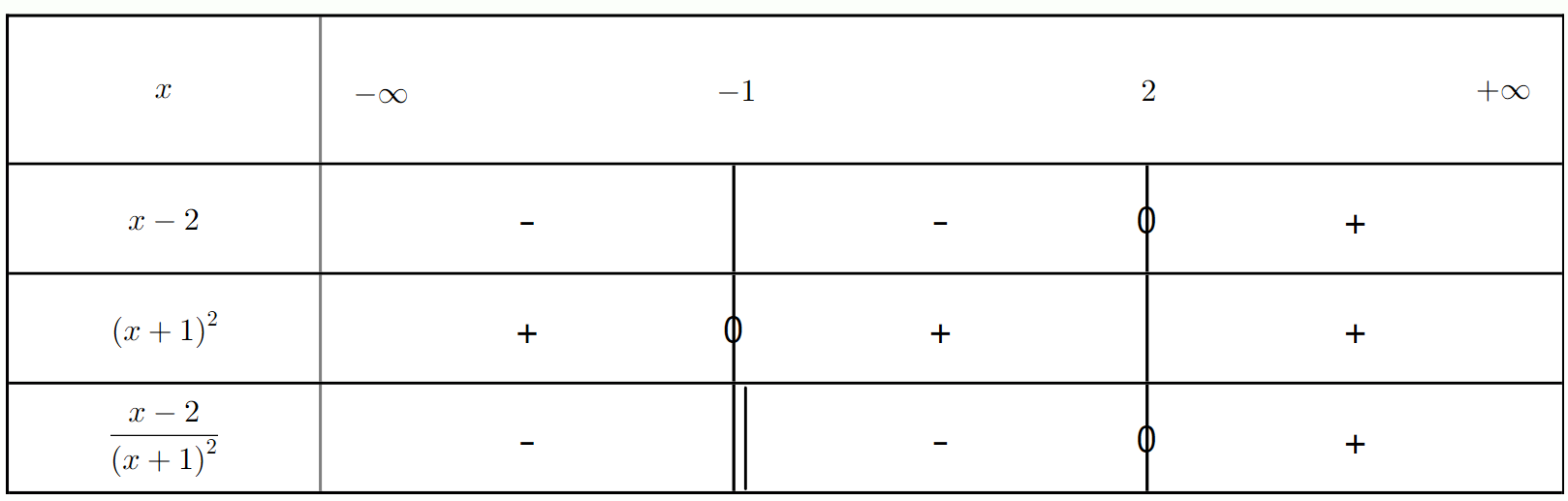
Résoudre l'inéquation $\frac{(x-2)}{(x+1)^2} \ge 0$
a) Déterminer les valeurs qui annulent chaque facteur.
b) Quelles sont les valeurs interdites ?
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment la double racine au dénominateur affecte-t-elle la valeur interdite et la solution ?
Exercice 15 : Inéquation produit avec des valeurs absolues (simplifiable)
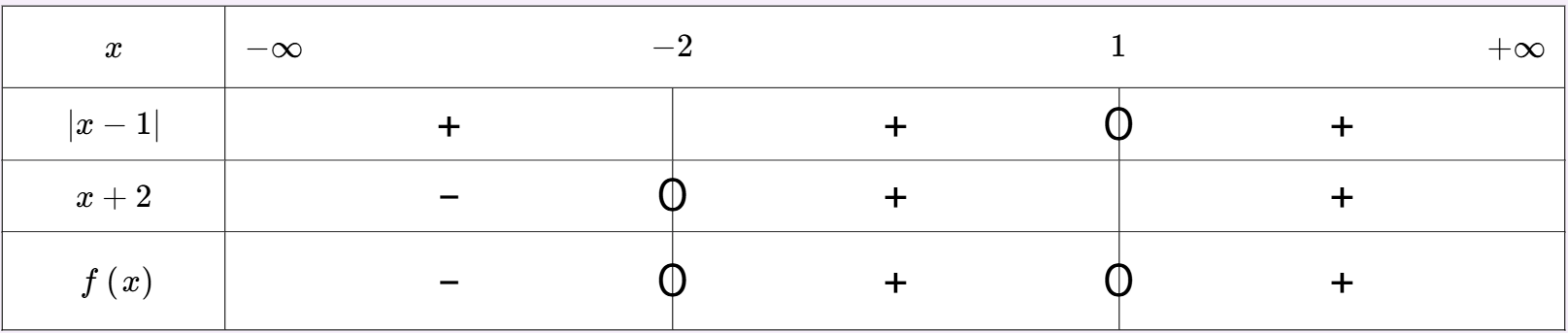
Résoudre l'inéquation $|x-1|(x+2)>0$
a) Quel est le signe de $|x-1|$ ?
b) Quelles sont les valeurs qui annulent chaque facteur ?
c) Établir le tableau de signes et en déduire l'ensemble des solutions.
d) Comment la valeur absolue simplifie-t-elle la résolution de l'inéquation ?
Exercice 16 : Inéquation quotient avec des valeurs absolues (simplifiable)
Résoudre l'inéquation $\frac{x+3}{|x-2|} < 0$
a) Quel est le signe de $|x-2|$ ?
b) Quelles sont les valeurs qui annulent chaque facteur ?
c) Quelles sont les valeurs interdites ?
d) Établir le tableau de signes et en déduire l'ensemble des solutions.
e) Comment la valeur absolue permet-elle de simplifier le tableau de signes ?
Exercice 17 : Application - Étude de signe d'une fonction
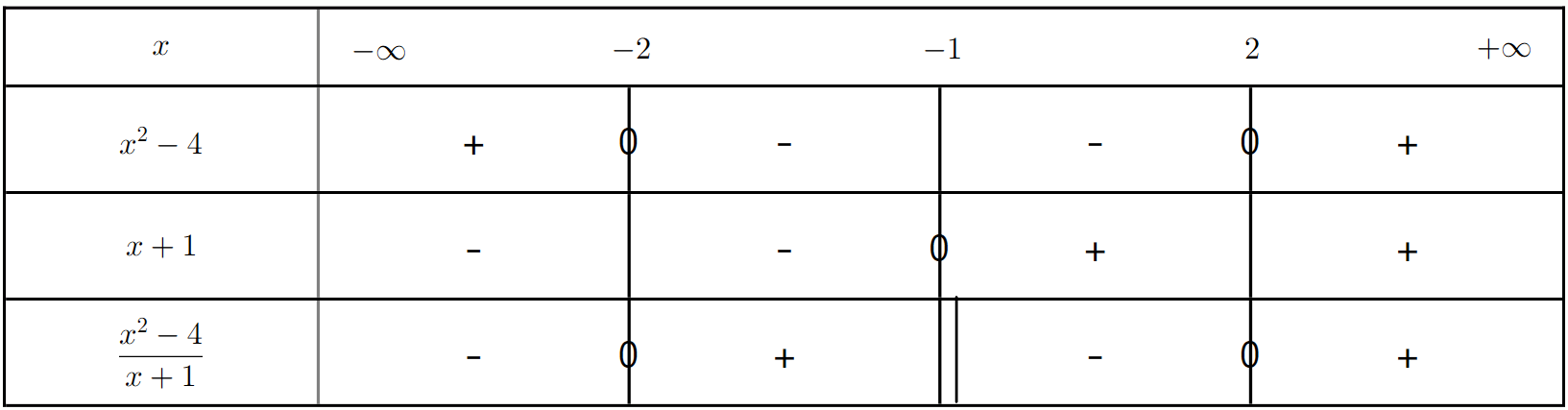
Soit la fonction $f(x) = \frac{x^2 - 4}{x + 1}$. Déterminer le signe de $f(x)$ sur $\mathbb{R} \setminus \{-1\}$.
a) Factoriser $x^2-4$.
b) Quelles sont les valeurs qui annulent chaque facteur ?
c) Quelle est la valeur interdite ?
d) Établir le tableau de signes et en déduire l'ensemble des intervalles où $f(x)$ est positive et où $f(x)$ est négative.
e) Comment l'étude du signe de la fonction peut-elle aider à résoudre des inéquations ?
Exercice 18 : Application - Comparaison de fonctions
Soit $f(x) = x^2$ et $g(x) = 2x + 3$. Déterminer les intervalles où $f(x) > g(x)$.
a) Déterminer l'expression de $f(x) - g(x)$.
b) Résoudre $f(x) > g(x)$.
c) Comment l'inéquation $f(x) > g(x)$ se traduit-elle graphiquement ?
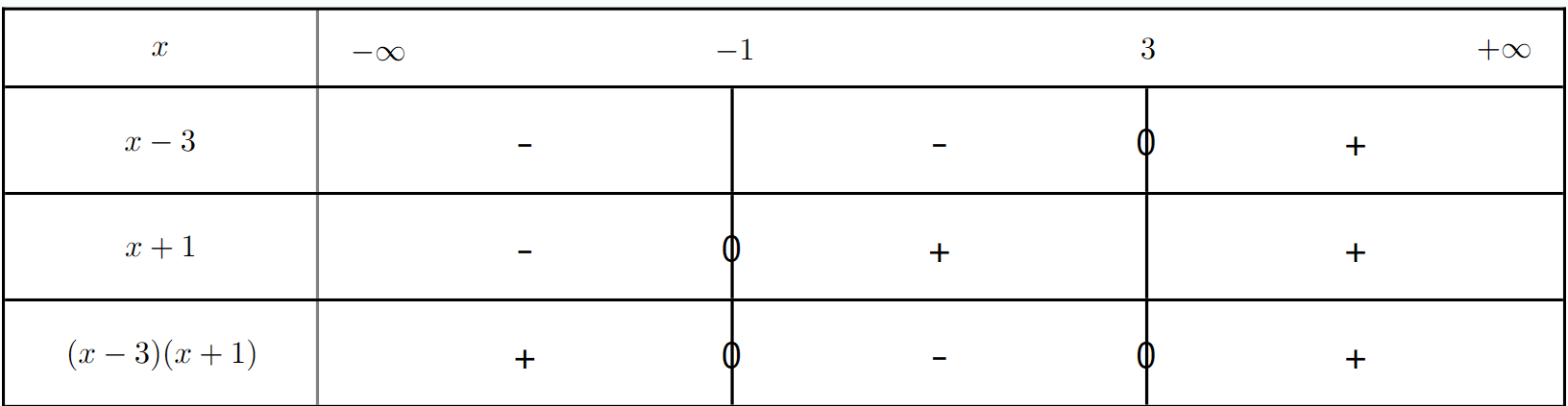
Exercice 19 : Inéquation produit avec polynôme du second degré (hors programme $\Delta$)
Résoudre l'inéquation $(x^2 - 5x + 6)(x + 1) \geq 0$.
a) Factoriser le polynôme $x^2 - 5x + 6$
b) Résoudre l'inéquation $(x^2 - 5x + 6)(x + 1) \geq 0$.
c) Comment les racines du polynôme du second degré influencent-elles la solution de l'inéquation ?
Exercice 20 : Inéquation quotient avec polynôme du second degré
Résoudre l'inéquation $\frac{x + 4}{x^2 - 3x + 2} \leq 0$.
a) Factoriser le polynôme $x^2 - 3x + 2$.
b) Résoudre l'inéquation $\frac{x + 4}{x^2 - 3x + 2} \leq 0$.
c) Comment identifier et traiter les valeurs interdites dans ce type d'inéquation ?
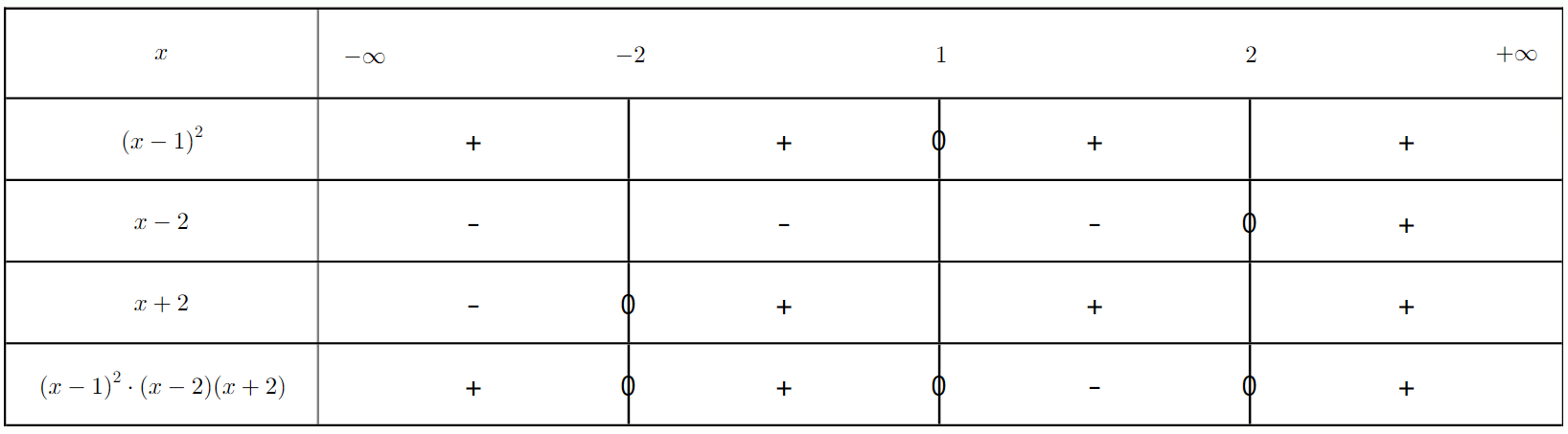
Exercice 21 : Inéquation produit avec un carré et un polynôme
Résoudre l'inéquation $(x-1)^2(x^2 - 4) \le 0$
a) Factoriser le polynôme $x^2-4$
b) Résoudre l'inéquation $(x-1)^2(x^2 - 4) \le 0$
c) Comment la présence du carré modifie-t-elle l'interprétation de la solution ?
Exercice 22 : Inéquation quotient avec un carré et un polynôme
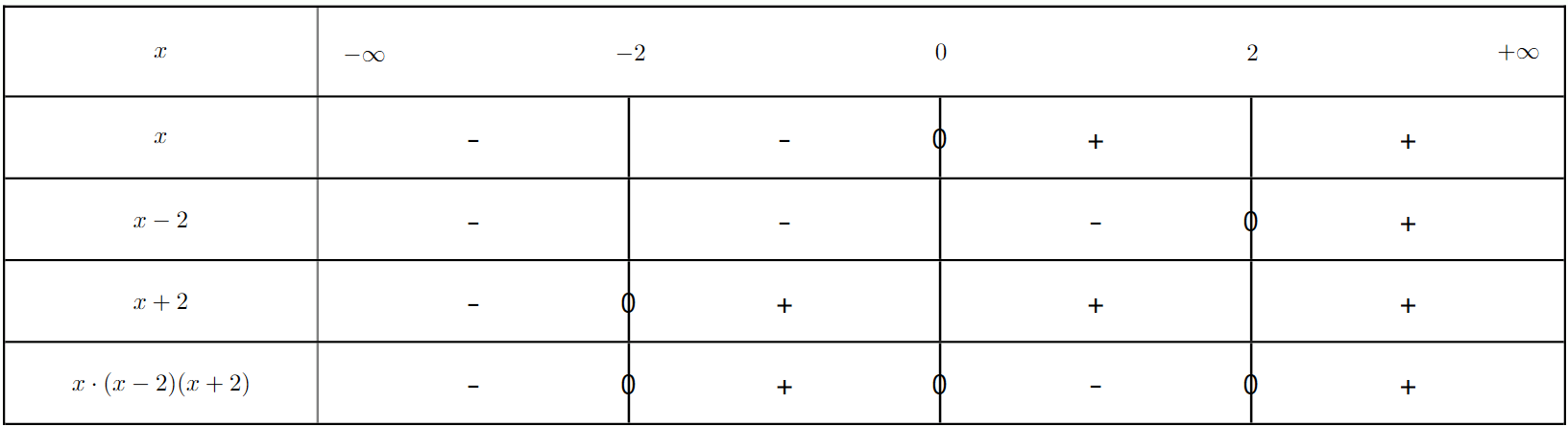
Résoudre l'inéquation $\frac{x^2 - 9}{(x+2)^2} \ge 0$
a) Factoriser le polynôme $x^2-9$
b) Résoudre l'inéquation $\frac{x^2 - 9}{(x+2)^2} \ge 0$
c) Comment traiter la valeur interdite lorsque le dénominateur est un carré ?
Exercice 23 : Résolution d'une inéquation avec des racines carrées (Application)
Déterminer les valeurs de $x$ pour lesquelles $\sqrt{x+1} < x-1$.
a) Quelles conditions doivent remplir $x$ pour que cette expression existe ?
b) Résoudre l'inéquation $\sqrt{x+1} < x-1$.
c) Pourquoi est-il important de vérifier les solutions obtenues après avoir élevé au carré ?
Exercice 24 : Étude de la position relative d'une courbe par rapport à une droite (Application)
Soit la fonction $f(x) = x^3 - 3x$ et la droite $d$ d'équation $y = x$. Déterminer les intervalles où la courbe représentative de $f$ est au-dessus de la droite $d$.
a) Que signifie le fait que la courbe soit au dessus de la droite d ?
b) Résoudre l'inéquation $f(x) > x$.
c) Comment l'étude des inéquations permet-elle de déterminer la position relative de deux courbes ?
Exercice 25 : Application - Optimisation d'une aire
Un agriculteur souhaite clôturer un enclos rectangulaire pour ses animaux. Il dispose de 100 mètres de clôture. On note $x$ la longueur d'un des côtés de l'enclos.
a) Exprimer la longueur de l'autre côté de l'enclos en fonction de $x$.
b) Exprimer l'aire $A(x)$ de l'enclos en fonction de $x$.
c) Quelles sont les valeurs possibles de $x$ (domaine de définition) ?
d) Pour quelle valeur de $x$ l'aire de l'enclos est-elle maximale ? (On pourra étudier le signe de $A(x) - A(25)$ )
e) Comment le domaine de définition influence-t-il la solution du problème d'optimisation ?
Exercice 26 : Application - Optimisation du prix d'un spectacle
Un organisateur de spectacles sait que s'il fixe le prix d'entrée à 20€, il aura 500 spectateurs. Il estime que chaque baisse de 1€ du prix d'entrée lui amènera 50 spectateurs supplémentaires. On note $x$ la baisse du prix d'entrée.
a) Exprimer le prix d'entrée en fonction de $x$.
b) Exprimer le nombre de spectateurs en fonction de $x$.
c) Exprimer la recette totale $R(x)$ en fonction de $x$.
d) Pour quelle valeur de $x$ la recette est-elle maximale ? On pourra chercher à factoriser $R(x) - R(15)$
e) Quelles sont les limites de ce modèle d'optimisation ?
Exercice 27 : Application - Fabrication de boîtes
On découpe aux quatre coins d'une plaque carrée de carton de 20 cm de côté, des carrés identiques de côté $x$. On replie ensuite les bords pour former une boîte sans couvercle.
a) Quelles sont les valeurs possibles de $x$ ?
b) Exprimer le volume $V(x)$ de la boîte en fonction de $x$.
c) Pour quelle valeur de $x$ le volume de la boîte semble-t-il maximal d'après la calculatrice ? (On ne demande pas de démonstration rigoureuse)
d) Comment le problème est-il contraint par les dimensions physiques de la plaque de carton ?
Exercice 28 : Application - Aire maximale d'un triangle
On considère un segment [AB] de longueur 10 cm. On place un point M sur ce segment. On construit un triangle AMN rectangle en A tel que $AM = x$ et $AN = 2x$ et un triangle MBQ tel que Q est rectangle en B et $BQ = 3(10-x)$
a) Exprimer l'aire du triangle AMN en fonction de $x$.
b) Exprimer l'aire du triangle MBQ en fonction de $x$.
c) Pour quelle valeur de $x$ la somme des aires est-elle minimale ?
d) Comment le problème est-il contraint par la longueur du segment [AB] ?
Exercice 29 : Application - Parcours minimal
Un randonneur doit se rendre d'un point A à un point B situés sur la même rive d'une rivière, distants de 6 km. Il peut marcher le long de la rive à une vitesse de 5 km/h, ou bien prendre un bateau qui va à 3 km/h. Sachant que le point B est situé à 6 km en aval de A, et que la rivière a une largeur constante de 2 km, déterminer où il doit accoster (point C) pour minimiser le temps total de parcours.
a) On note $x$ la distance entre le point A et le point C ou il accoste. Donner les valeurs de $x$ possible.
b) Exprimer le temps mis pour parcourir AC à pied, et le temps mis pour parcourir CB en bateau.
c) En déduire une expression du temps total, et déterminer pour quelle valeur de $x$ ce temps est minimal (on admettra que cette valeur minimise le temps).
d) Comment la vitesse du bateau et la vitesse de marche influencent-elles le point d'accostage optimal ?
Exercice 30 : Production de pâte à papier
Une entreprise fabrique et vend de la pâte à papier. Le coût de production de $q$ tonnes de pâte à papier est donné, en milliers d'euros, par $C(q) = 0.02q^2 + 0.1q + 9$ pour $q \in [0; 80]$. La recette, en milliers d'euros, engendrée par la vente de $q$ tonnes de pâte à papier est donnée par $R(q) = 1.2q$.
(a) Quel est le coût de fabrication d'une tonne de pâte à papier ?
(b) Quel est le prix de vente d'une tonne de pâte à papier ?
(c) L'entreprise est-elle bénéficiaire lorsqu'elle vend et produit une tonne de pâte à papier ?
2. Avec la calculatrice, conjecturez pour quelles quantités de pâte à papier l'entreprise est bénéficiaire.
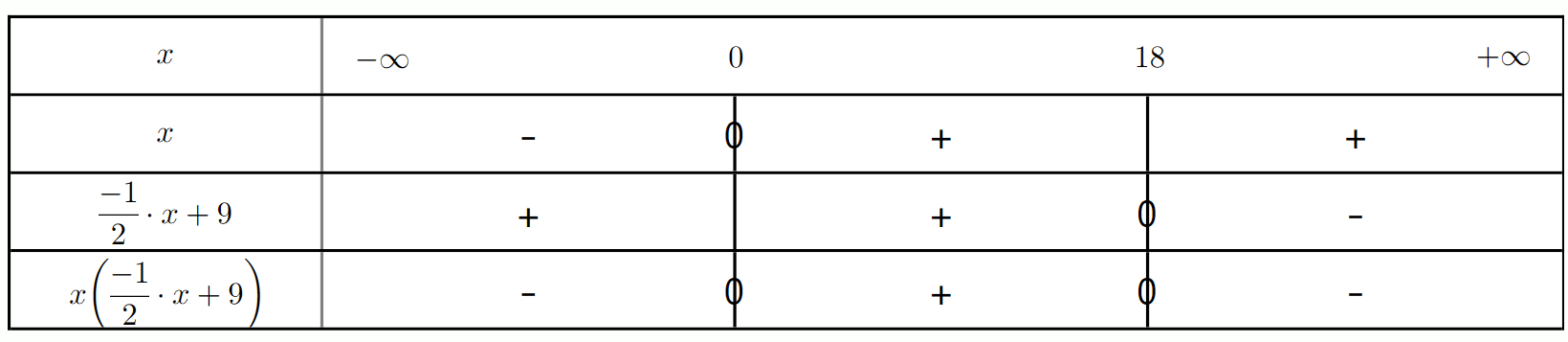
3. Démontrez que le bénéfice, en milliers d'euros, est $B(q) = -0.02q^2 + 1.1q - 9$.
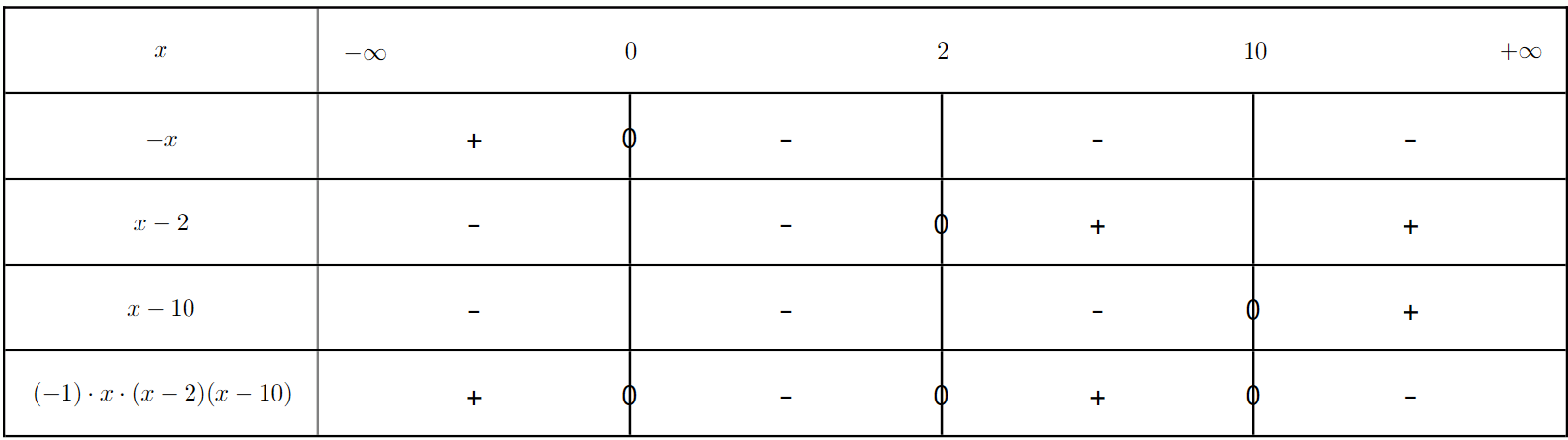
4. Démontrez que $B(q) = -0.02(q - 45)(q - 10)$ pour tout $q \in [0; 80]$.
5. Déterminez pour quelles quantités l'entreprise est bénéficiaire.
Exercice 31 : Production d'un produit
Une entreprise fabrique un produit. Pour une période donnée, le coût total de production, en euros, est donné en fonction du nombre $q$ d'articles fabriqués par : $C(q) = 2q^2 + 10q + 900$ pour $0 \le q \le 80$. Tous les articles fabriqués sont vendus. La recette totale, en euros, est donnée par $R(q) = 120q$.
1. Vérifiez que le bénéfice total est donné par $B(q) = -2q^2 + 110q - 900$.
Puis que la forme factorisée de $B(q)$ est : $B(q) = -2(q - 10)(q - 45)$.
2. Pour quels nombres d'articles produits la production est-elle rentable ?
Exercice 32 : Production et vente d'un produit
Une entreprise fabrique et vend un produit. On note $f(x)$ le coût de production, exprimé en milliers d'euros, de $x$ tonnes de ce produit. Pour $0 \le x \le 11$, des études ont montré que : $f(x) = x^3 - 12x^2 + 50x$. L'entreprise vend son produit 30000 euros la tonne. On note $g(x)$ la recette exprimée en milliers d'euros et $B(x)$ le bénéfice : $B(x) = g(x) - f(x)$.
1. Exprimez $g(x)$ en fonction de $x$.
2. Développez, réduisez et ordonnez $B(x)$.
3. Développez, réduisez et ordonnez $(x - 2)(x - 10)$.
4. Résolvez l'inéquation $B(x) \ge 0$.
5. Interprétez le résultat.
Exercice 33
Soient $f$ et $g$ des fonctions définies sur $\mathbb{R}$ par $f(x) = x^2$ et $g(x) = 2x + 1$.
1. Vérifiez que pour tout réel $x$, $f(x) - g(x) = (x - 1)^2 - 2$.
2. Résolvez l'inéquation $f(x) \le g(x)$.
Exercice 34
Soit un réel $x$ dans l'intervalle $[0; 8]$. On considère un rectangle de dimension 4 cm sur $x$ cm, dans lequel on trace deux disques de même rayon comme sur la figure ci-contre.
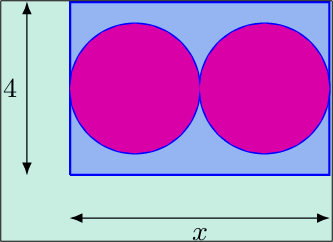
On souhaite déterminer les valeurs de $x$ de façon que l'aire bleue (ce qu'il reste du rectangle) soit supérieure à l'aire rose (les deux disques).
1. Montrez que le problème se ramène à la résolution de l'inéquation $\frac{\pi}{8}x^2 - 2x \le 0$ sur $[0; 8]$.
2. Montrez que l'ensemble des solutions est $\left[0; \frac{16}{\pi}\right]$.
Exercice 35 : Application - Aire maximale d'un rectangle dans un triangle
Soit un triangle ABC rectangle en A avec $AB = 6$ cm et $AC = 8$ cm. On inscrit un rectangle ADEF dans ce triangle tel que D est sur [AB], E sur [BC] et F sur [AC]. On pose $AD = x$.
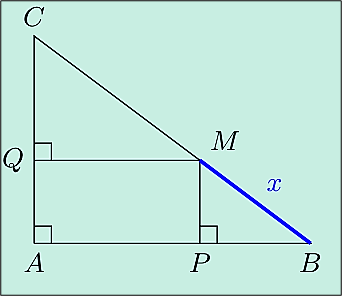
a) Quelles sont les valeurs de $x$ possible ?
b) Exprimer $DE$ en fonction de $x$.
c) Exprimer l'aire du rectangle ADEF en fonction de $x$.
d) Pour quelle valeur de $x$ l'aire du rectangle est-elle maximale ?
e) Comment les dimensions du triangle ABC influencent-elles l'aire maximale du rectangle ?
Exercice 36 : Application - Baignade surveillée
Une zone de baignade est délimitée par deux bouées A et B, distantes de 20 mètres. Un poste de secours est placé entre les bouées. $x$ est la distance entre la bouée A et le poste de secours. Le sauveteur nage deux fois moins vite qu'il ne court.
a) Valeurs possibles de $x$ ?
b) Un baigneur est en difficulté à 8 mètres de A sur la plage et à 4 mètres du large. Temps du sauveteur en fonction de $x$ ?
c) Valeur de $x$ qui minimise le temps (calculatrice) ?
d) Influence de la position du baigneur ?
Exercice 37 : Application - Aire d'un carré inscrit
Dans un carré ABCD de côté 20 cm, on inscrit un carré MNPQ suivant le schéma ci-contre. On pose $x = AM = BN = CP = DQ$ avec $0 \le x \le 20$.
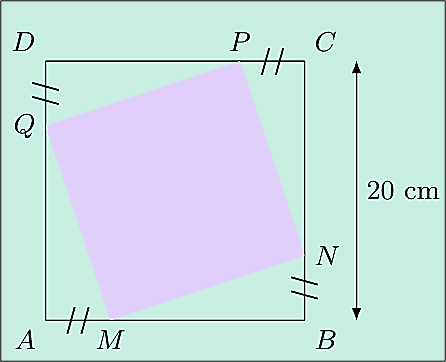
Le but de cet exercice est de déterminer les valeurs de $x$ pour lesquelles l'aire du carré MNPQ dépasse 272 cm².
1. Exprimez l'aire, en cm², $g(x)$ du carré MNPQ en fonction de $x$, sous forme développée, ordonnée et réduite.
2. Prouvez que $g(x) > 272$ équivaut à $2x^2 - 40x + 128 > 0$.
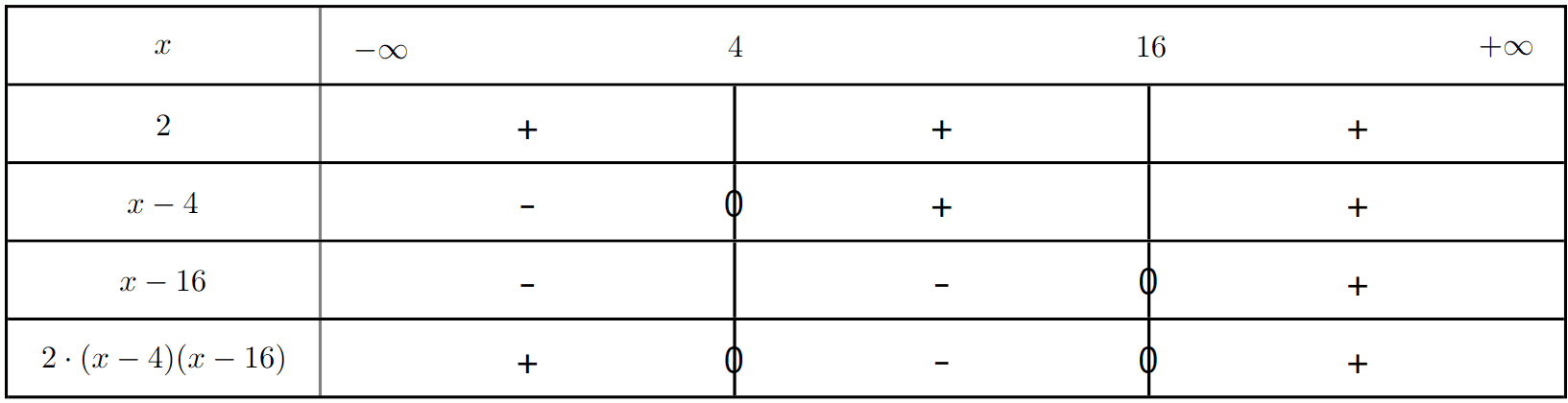
3. On note $f(x) = 2x^2 - 40x + 128$. Affichez sur votre calculatrice la courbe représentative de $f$, tracez à main levée la courbe observée puis conjecturez les solutions du problème. (Fenêtre : abscisses 0 à 20, ordonnées -100 à 200).
4. On se propose de retrouver le résultat par le calcul.
(a) Vérifiez que $f(x) = 2(x - 4)(x-16)$.
(b) Étudiez le signe de $f(x)$.
(c) Déduisez-en les solutions du problème.
Exercice 38 : Application - Aire d'un triangle dans un carré
ABCD est un carré de côté $x$, exprimé en cm, avec $x > 6$. E est le point du segment [AB] tel que $EB = 6$ cm.
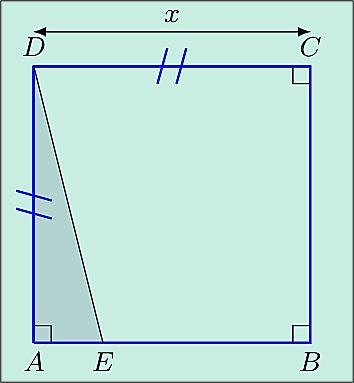
1. Exprimez en fonction de $x$, l'aire en cm² du triangle AED.
2. Peut-on trouver $x$ pour que l'aire du carré ABCD soit strictement supérieure au triple de l'aire du triangle AED?