Revoyons ensemble les points essentiels sur les Proportions avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Définition d'une proportion
Une proportion représente une fraction d'un tout. Elle peut être exprimée sous différentes formes : fraction ($\frac{a}{b}$), nombre décimal (0,a), ou pourcentage ($p\%$). L'important est de comprendre que ça représente toujours une partie par rapport à un ensemble total.
2. Calculer une proportion
Pour calculer une proportion, on utilise la formule de base :
$\text{Proportion} = \frac{\text{Partie}}{\text{Total}}$
N'oubliez pas de bien identifier la "partie" et le "total" dans l'énoncé de l'exercice. Pour l'exprimer en pourcentage, on multiplie le résultat par 100.
3. Appliquer une proportion
Appliquer une proportion, c'est calculer une partie à partir du total et de la proportion. Si on connaît la proportion $p$ et le total $T$, alors la partie $P$ est donnée par :
$\text{Partie} = \text{Proportion} \times \text{Total}$
Par exemple, si $25\%$ des 800 personnes habitent en zone rurale, le nombre de personnes en zone rurale est $0,25 \times 800 = 200$.
4. Proportions successives
Quand on a des proportions de proportions (par exemple, $60\%$ des films d'action sont avec Bruce Willis, et les films d'action représentent $30\%$ du serveur), pour trouver la proportion finale (films avec Bruce Willis par rapport au serveur total), on multiplie les proportions entre elles. C'est comme prendre une fraction d'une fraction.
5. Tableaux et proportions
Les tableaux sont souvent utilisés pour organiser des données et faciliter les calculs de proportions. Ils aident à visualiser les "parts" et les "totaux" et à appliquer les formules correctement. Remplir un tableau de proportions, c'est exprimer chaque effectif comme une proportion du total correspondant.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
On appelle « téléviseur 16/9 » un téléviseur dont la longueur de l'écran est égale aux $\dfrac{16}{9}$ de sa largeur.
Pour un tel téléviseur, calculer le longueur de l'écran lorsque la largeur est $41,4\ \mathrm{cm}$.
Exercice 2
Pour 1080 francs, le père de Pierre a acheté $4$ cravates et $3$ chemises.
Sachant que le prix d'une cravate est les $\dfrac{3}{5}$ de celui d'une chemise: quels sont les prix d'une cravate et d'une chemise?
Exercice 3
Dans deux classes de 24 élèves chacun, on demande aux collégiens combien de temps ils passent dans l'autobus pour se rendre au collège (tous prennent l'autobus).
1. Sachant que tous les élèves ont répondu, reproduire et compléter le tableau ci-dessous présentant les résultats de cette enquête:
| Temps $t$ en $\mathrm{min}$ | $0 \leqslant t <15$ | $15 \leqslant t <30$ | $30 \leqslant t <45$ | $t \geqslant 45$ |
|---|---|---|---|---|
| Effectif | $6$ | $24$ | $3$ |
2. Quel est l'effectif d'élèves passant au moins $30$ minutes dans l'autobus pour se rendre au collège?
3. En déduire le pourcentage d'élèves passant au moins une demi-heur dans l'autobus pour se rendre au collège.
Exercice 4
Le tableau ci-dessous indique, en 1982, le bilan des accidents corporel de la circulation dans un pays. Compléter le tableau. Chaque résultat pour les pourcentages sera arrondi au dixième près.
| Nombre des tués | Nombre de blessés légers | Nombre de blessés graves | Nombre total d'accidentés | |
|---|---|---|---|---|
| Effectifs | 12500 | 321000 | 84500 | 418000 |
| Pourcentages |
Exercice 5
Dans une classe de première de 35 élèves, 9 élèves font du ski.
Calculez le pourcentage d'élèves de la classe qui font du ski arrondi à $10^{-2}$ près.
Exercice 6
Une salle de spectacle contient 9000 places assises et 21000 places debout.
1. Calculez le pourcentage de places assises.
2. Déterminez le pourcentage de places debout.
Exercice 7
1. Dans un petit port, les cinq-sixièmes des 720 habitants vivent de la pêche. Combien d'habitants vivent de la pêche?
2. Dans un village voisin, 697 habitants vivent de l'agriculture, ce qui représente $82\%$ de la population. Combien y a-t-il d'habitants dans ce village?
Exercice 8
Un marchand a des crayons bleus, des crayons rouges et crayons verts. Les crayons bleus représentent $53\%$ de la totalité des crayons.
Les crayons rouges représentent les $\dfrac{3}{10}$ de la totalité des crayons.
1. Les crayons verts représentent un pourcentage de la totalité des crayons. Quel est ce pourcentage?
2. En tout le marchand a $300$ crayons. Combien a-t-il de crayons bleus?
Exercice 9
1. Une année le taux de réussite au baccalauréat technologique est de $79,7\%$, ce qui représente 129979 candidats reçus.
Calculez le nombre de candidats à cet examen.
2. Dans un lycée le taux de réussite est de $95\%$, et il y a eu $12$ refusés.
Calculez le nombre de candidats dans ce lycée.
Exercice 10
Le salaire brut mensuel de Sophie est de 13200 euros. Les cotisations salariales représentent $23\%$ du salaire brut.
Calculez le salaire hors cotisations salariales.
Exercice 11
Le tableau suivant donne le mode de transport des 1292 salariés d'une entreprise pour se rendre à leur travail. On note:
• $A$ l'ensemble des employés qui utilisent les transports en commun, • $B$ l'ensemble des employés qui viennent à pied, • $C$ l'ensemble des employés qui utilisent leur voiture, • $H$ l'ensemble des hommes.
| $H$ | $\overline{H}$ | |
|---|---|---|
| $A$ | $210$ | $380$ |
| $B$ | $52$ | $80$ |
| $C$ | $450$ | $120$ |
1. Recopiez ce tableau en indiquant le pourcentage d'employés plutôt que le nombre d'employés.
2. Expliquez ce qu'est l'ensemble $\overline{H}$.
3. Calculez la proportion d'hommes dans l'entreprise.
4. Expliquez ce qu'est $A \cap H$ puis calculez le pourcentage d'employés dans cet ensemble.
5. Expliquez ce qu'est $C \cap \overline{H}$ puis calculez le pourcentage d'employés dans cet ensemble.
6. Expliquez ce qu'est $\overline{C}$ puis calculez le pourcentage d'employés dans cet ensemble.
Exercice 12
Un institut de sondage a interrogé $800$ personnes des la manière suivante:
• $25\%$ des personnes interrogées habitent en zone rurale, les autres en zone urbaine;
• $60\%$ des personnes interrogées ont été consultées par téléphone, les autres personnes ayant été interrogées en « face à face » par un enquêteur;
• $55\%$ des personnes habitant en zone urbaine ont été consultées par téléphone.
1. Reproduisez et complétez le tableau d'effectifs suivant:
| Habitant en zone rurale | Habitant en zone urbaine | Total | |
|---|---|---|---|
| Personnes interrogées par téléphone | |||
| Personnes interrogées en « face à face » | |||
| Total | $200$ | $800$ |
2.
a) Calculez la proportion de personnes habitant en zone urbaine parmi celles qui ont été consultées par téléphone: donner le résultat sous la forme d'un nombre décimal, puis sous la forme d'un pourcentage.
b) Calculez la proportion de personnes habitant en zone urbaine parmi celles interrogées en « face à face »: donner le résultat sous la forme d'un nombre décimal arrondi à $10^{-4}$ près, puis sous la forme d'un pourcentage.
c) L'ordre des proportions (ou fréquences) obtenues en (a) et en (b) est-il le même que celui des effectifs des sous-populations correspondantes?
Exercice 13
Un restaurant sert $600$ couverts par service, en proposant un menu à $16$ euros et un menu à $24$ euros. Pour l'inauguration de son restaurant, le gérant offre à chacun de ses clients soit un café, soit un apéritif.
• $60\%$ des clients ont choisi un café, les autres un apéritif.
• La moitié des clients ont choisi un menu à $24$ euros.
• Parmi ceux qui choisissent le menu à $24$ euros, $75\%$ ont choisi un café.
1. Complétez après l'avoir reproduit le tableau suivant:
| Menu à 16 euros | Menu à 24 euros | Total | |
|---|---|---|---|
| Clients ayant choisi un café | $360$ | ||
| Clients ayant choisi un apéritif | |||
| Total | $600$ |
2. On note $A$ la sous-population des clients ayant choisi un menu à $16$ euros et $B$ la sous-population des clients ayant choisi un apéritif.
a) Définissez par une phrase les sous-populations $A \cap B$ et $A\cup B$.
Dans ce qui suit les résultats seront donnés sous forme de fractions irréductibles.
b) Calculez les proportions (ou fréquences) respectives, notées $P(A)$, $P(B)$, $P(A\cap B)$ et $P(A \cup B)$, des sous-populations $A$, $B$, $A \cap B$ et $A \cup B$ dans la population des $600$ couverts.
c) Calculez $P(A)+P(B)-P(A \cap B)$. Que remarquez-vous?
d) On note $C$ la sous-population des clients ayant choisi un café. On note $P(C)$ la proportion de la sous-population $C$ dans la population des $600$ couverts. Les deux sous-populations $A$ et $C$ sont-elles disjointes? Même question pour les deux sous-populations $B$ et $C$. Calculez $P(B)+ P(C)$.
Exercice 14
Un magasin vend deux types de téléphones mobiles: des modèles $m_1$ et des modèles $m_2$.
Ce magasin propose deux types de forfait mensuel: un forfait $1$ et un forfait $2$.
Le service commercial effectue une enquête sur un échantillon de 2000 clients ayant acheté dans ce magasin un téléphone et un seul, et ayant opté pour un seul des forfaits proposés.
Sur les 2000 clients interrogés, 1200 ont acheté le modèle $m_1$ et 960 ont choisi le forfait $F_1$.
Parmi les clients ayant acheté le modèle $m_1$, $32\%$ ont pris le forfait $F_1$.
1. Complétez après l'avoir reproduit, le tableau d'effectifs suivant:
| Modèle $m_1$ | Modèle $m_2$ | Total | |
|---|---|---|---|
| Forfait $1$ | $960$ | ||
| Forfait $2$ | |||
| Total | $1200$ | $2000$ |
2. On note $F_1$ la sous-population des clients interrogés ayant choisi le forfait $1$ et $M_2$ la sous-population ayant choisi le modèle $m_2$.
a) Calculez, sous la forme d'un nombre décimal, la proportion $P(F_1)$ de clients interrogés qui ont choisi le forfait $1$.
b) Calculez, sous la forme d'un nombre décimal, la proportion $P(M_2)$ de clients ayant choisi le modèle $m_2$.
c) Définissez par une phrase en français les sous-populations $F_1 \cap M_2$ et $F_1 \cup M_2$.
d) Calculez, sous la forme d'un nombre décimal, la proportion $P(F_1 \cap M_2)$ de clients qui appartiennent à la sous-population $F_1 \cap M_2$ parmi les clients interrogés.
e) Déduisez de ce qui précède la proportion $P(F_1 \cup M_2)$ de clients qui appartiennent à la sous-population $F_1 \cup M_2$ parmi le clients interrogés: sous la forme d'un nombre décimal puis sous la forme d'un pourcentage.
Exercice 15
Un serveur de films en streaming est composé de $30\%$ de films d'action et, parmi ces films d'action, $60\%$ sont des films avec Bruce Willis.
Quelle est la proportion de films avec Bruce Willis sur le serveur?
Exercice 16
Dans une classe $45\%$ des élèves sont des garçons et $\frac{1}{3}$ des garçons portent des lunettes.
Il y a $3$ garçons à lunettes dans la classe.
1. Combien y a-t-il d'élèves dans cette classe?
2. Combien y a-t-il de filles dans cette classe?
Exercice 17
Dans une société les cadres représentent $40\%$ des salariés et les cadres supérieurs représentent un $20\%$ des cadres.
Quelle est la proportion de cadres supérieurs par rapport aux salariés de cette société?
Exercice 18
Une société de téléphonie propose trois mode d'abonnement différents:
• forfait $A$: moins de $2\ \mathrm{h}$ de communication;
• forfait $B$: moins de $4\ \mathrm{h}$ de communication;
• forfait $C$: temps de communication illimité.
La part de clients ayant souscrit le forfait $A$ est de $0,35$ et les clients ayant choisi le forfait $B$ représentent la moitié de la clientèle.
De plus $80\%$ des clients ayant choisi le forfait $C$ ont également choisi l'internet illimité.
1. Quelle est la part de clients ayant choisi le forfait illimité? Exprimez ce résultat en pourcentage.
2. Quelle est la part des clients qui ont choisi un forfait $C$ mais sans l'internet illimité.
Exercice 19
Une entreprise est composée de trois services: Administratif, Logistique et Transport. $45\%$ des employés travaillent au sein du service Administratif et $23\%$ au sein du service Logistique. Une enquête effectuée sur le temps de trajet quotidien entre le domicile des employés et l'entreprise a montré que:
• $54,2\%$ des employés résident à moins de $30\ \mathrm{min}$ de l'entreprise;
• $60\%$ des employés du service Logistique résident à moins de $30\ \mathrm{min}$ de l'entreprise;
• $9,6\%$ des employés travaillent au sein du service Transport et résident à $30\ \mathrm{min}$ ou plus de l'entreprise.
1. Reproduisez et complétez le tableau ci-dessous à l'aide des pourcentages donnés dans l'énoncé.
| Service Administratif | Service Logistique | Service Transport | Total | |
|---|---|---|---|---|
| Résidant à moins de $30\ \mathrm{min}$ | ||||
| Résidant à $30\ \mathrm{min}$ ou plus | ||||
| Total | $45\%$ | $23\%$ | $100\%$ |
2. Détermine, au sein du service Administratif, puis au sein du service Transport, la proportion (en $\%$) des employés qui résident à moins de $30\ \mathrm{min}$ de l'entreprise.
3.
a) Quel service a la plus forte proportion d'employés qui résident à moins de $30\ \mathrm{min}$ de l'entreprise?
b) Quel service a la plus forte proportion d'employés qui résident à $30\ \mathrm{min}$ ou plus de l'entreprise?
Exercice 20
Un cube a une arêtes de $8\ \mathrm{cm}$. Un cône de révolution a une base de $8\ \mathrm{cm}$ de diamètre et une hauteur de $8\ \mathrm{cm}$.
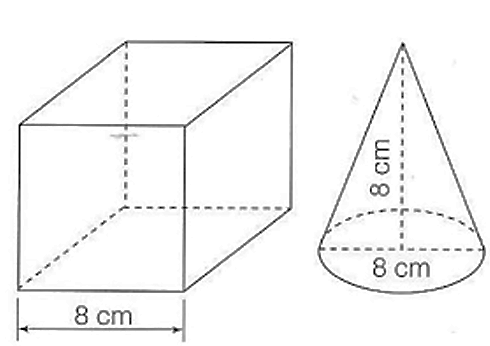
1. Calculez le volume du cube.
2.
a) Calculez la valeur exacte du volume du cône.
b) Quel est le volume du cône arrondi au $\mathrm{cm}^3$ ?
3. On place le cône à l'intérieur du cube. Occupe-t-il plus de $30\%$ du volume du cube? Justifiez votre réponse.
Exercice 21
Vrai ou faux?
Armelle et Boris ne suivent pas les mêmes enseignements. La semaine $1$, Armelle a réussi $50\%$ des exercices qu'elle a traités et Boris $90\%$ des exercices qu'il a traités.La semaine $2$, Armelle a réussi $20\%$ des exercices qu'elle a traités et Boris $40\%$ des exercices qu'il a traités.
Sur l'ensemble de la quinzaine, Boris a nécessairement réussi un plus grand pourcentage d'exercices traités qu'Armelle.