Revoyons ensemble les points essentiels sur les Inéquations du Premier Degré et les Intervalles avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Inéquations du Premier Degré : Principes de Résolution
Définition : Une inéquation du premier degré est une inégalité qui peut être mise sous la forme $ax + b \leq 0$ (ou avec les symboles $\lt, \geq, \gt$).
Principes de résolution : Similaires à ceux des équations, mais attention aux opérations qui changent le sens de l'inégalité :
Addition/Soustraction : Ajouter ou soustraire un même nombre aux deux membres ne change pas le sens de l'inégalité.
Exemple : $x - 3 < 7 \Leftrightarrow x < 7 + 3 \Leftrightarrow x < 10$.
Multiplication/Division par un nombre positif : Multiplier ou diviser par un nombre positif ne change pas le sens de l'inégalité.
Exemple : $2x < 8 \Leftrightarrow x < \frac{8}{2} \Leftrightarrow x < 4$.
Multiplication/Division par un nombre négatif : Multiplier ou diviser par un nombre négatif inverse le sens de l'inégalité.
Exemple : $-2x < 6 \Leftrightarrow x > \frac{6}{-2} \Leftrightarrow x > -3$.
Ensemble de solutions : Les solutions d'une inéquation du premier degré sont généralement un intervalle ou une réunion d'intervalles de nombres réels.
2. Intervalles : Notation et Représentation
Définition : Un intervalle est un ensemble de nombres réels compris entre deux bornes.
Notations :
Intervalle fermé $[a, b]$ : Inclut les bornes $a$ et $b$. Correspond à $a \leq x \leq b$.
Intervalle ouvert $]a, b[$ : Exclut les bornes $a$ et $b$. Correspond à $a < x < b$.
Intervalles semi-ouverts/fermés $]a, b]$ ou $[a, b[$ : Incluent une borne et excluent l'autre. Correspond à $a < x \leq b$ ou $a \leq x < b$.
Intervalles infinis : $]-\infty, a]$, $]-\infty, a[$, $[a, +\infty[$, $]a, +\infty[$, $\mathbb{R} = ]-\infty, +\infty[$. Utilisent l'infini ($\infty$) pour indiquer une borne non limitée.
Représentation graphique : Les intervalles sont représentés sur la droite réelle par des segments (ou demi-droites) avec des crochets indiquant si les bornes sont incluses ou exclues.
3. Combinaison d'Inégalités et Systèmes d'Inéquations
Systèmes d'inéquations : Pour résoudre un système de plusieurs inéquations, il faut résoudre chaque inéquation séparément, puis trouver l'intersection de leurs ensembles de solutions.
Intersection d'intervalles : L'intersection de deux intervalles est l'ensemble des nombres qui appartiennent à la fois à tous les intervalles du système. Graphiquement, c'est la partie commune aux intervalles sur la droite réelle.
Utilisation de tableaux de signes : Pour les inéquations produits ou quotients, un tableau de signes est indispensable pour analyser le signe de chaque facteur et du produit/quotient sur différents intervalles, et ainsi déterminer l'ensemble des solutions.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Intervalles
Exercice 1 : Placement de points sur une droite numérique
Tracez une droite numérique et placez les points suivants d'après leurs abscisses :
a) $O(0)$
b) $I(1)$
c) $A(-6)$
d) $B(2)$
e) $C(-1)$
f) $D(1,5)$
g) $E\left( -\frac{1}{2} \right)$
h) $F\left( 2^2 \right)$
i) $G\left((-2)^2 \right)$
j) $J\left( \sqrt{9} \right)$
k) $K\left( \frac{1}{3} \right)$
l) $L\left(-5+\sqrt{7} \right)$
Exercice 2 : Représentation d'intervalles sur une droite numérique
À chaque fois, tracez la droite numérique en choisissant $OI$ égale à 1 carreau, puis dessinez l'intervalle proposé :
a) $I_1=[-3;0]$
b) $I_2=[2,4]$
c) $I_3=]-2;1]$
d) $I_4=[2,+\infty[$
e) $I_5=]-\infty, -1]$
f) $I_6= \left[ -\frac{1}{3},4\right[$
g) $I_7= ]-4;3[$
h) $I_8= \left] \sqrt{2},+\infty\right[$
i) $I_9= ]-\infty, -4[$
Exercice 3 : Intervalles en langage courant
À chaque fois, tracez la droite numérique en choisissant $OI$ égale à 1 carreau, puis dessinez l'intervalle proposé décrit en français :
a) "L'intervalle ouvert en $-1$, fermé en $0$".
b) "L'intervalle fermé en $-2$ et en $3$".
c) "L'intervalle fermé en $-4$, $+\infty$".
d) "L'intervalle ouvert en $4$, $+\infty$".
e) "L'intervalle $-\infty$, fermé en $3$".
f) "L'intervalle fermé en $-4$ et ouvert en $2$".
g) "L'intervalle fermé en $-4$, $+\infty$".
h) "L'intervalle $-\infty$, ouvert en $3$".
i) "L'intervalle fermé en $-4$, ouvert en $-1$".
Exercice 4 : Appartenance à un intervalle
Dites à chaque fois si le nombre $a$ appartient à l'intervalle $I$ ou pas :
a) $a=-1$ et $I=]-\infty,-2]$
b) $a=\pi$ et $I=[3,05:3,8]$
c) $a=-3$ et $I=[-3,245;+\infty[$
d) $a=\frac{1}{3}$ et $I= \left[ 0; \frac{1}{2} \right]$
e) $a=10^3$ et $]1000;+\infty[$
f) $a=-\frac{1}{4}$ et $I= \left]-\frac{1}{3},0 \right[$
g) $a=-2$ et $I=[-4;-2[$
Exercice 5 : Traduction d'inégalités en intervalles
Traduisez la ou les inégalités par une appartenance à un intervalle :
a) $-6>x$
b) $12\leqslant x \leqslant 100$
c) $-3< x \leqslant 11$
d) $-11\leqslant x<-1$
e) $8>x>\frac{1}{2}$
f) $4\leqslant x$
g) $x\geqslant 10^{-3}$
Exercice 6 : Complétez le tableau sur les intervalles (1/2)
Recopiez le tableau, puis complétez-le en prenant pour modèle la deuxième ligne :
| Notation | Inéquations (encadrement) | Description |
|---|---|---|
| $[-2 ;13]$ | $-2\le x \le 13$ | Intervalle fermé en $-2$ et en $13$. |
| $[4\ ;\ 8[$ | $\dots$ | $\dots$ |
| $]-\infty\ ;\ -5]$ | $\dots$ | $\dots$ |
| $[\pi \ ;\ 8[$ | $\dots$ | $\dots$ |
| $]-6\ ;\ 2]$ | $\dots$ | Intervalle ouvert en $-6$ et fermé en $2$. |
Exercice 7 : Complétez le tableau sur les intervalles (2/2)
Recopiez le tableau, puis complétez-le en prenant pour modèle la deuxième ligne :
| Notation | Inéquations (encadrement) | Description |
|---|---|---|
| $[-2 , +\infty [$ | $-2\le x$ | Intervalle fermé en $-2$, plus l'infini. |
| $] -\infty ;\ 8[$ | $\dots$ | $\dots$ |
| $] -3\ ;\ +\infty[$ | $\dots$ | $\dots$ |
| $] -\infty\ ;\ -6[$ | $\dots$ | Intervalle moins l'infini, ouvert en $-6$. |
Exercice 8 : Complétez le tableau récapitulatif sur les intervalles
Complétez le tableau ci-dessous (les schémas ne doivent pas être à l'échelle) :
| Notation | Inéquation(s) | Description |
|---|---|---|
| $]-2\ ;\ +\infty[$ | $\dots$ | $\dots$ |
| $\dots$ | $\dots$ | $\dots$ |
| $]-3\ ;\ 4]$ | $-3 < x \le 4$ | $\dots$ |
| $\dots$ | $\dots$ | Intervalle ouvert en $-5$ et fermé en $7$. |
Exercice 9 : Distances et intervalles sur une figure géométrique
On considère la figure ci-dessous :
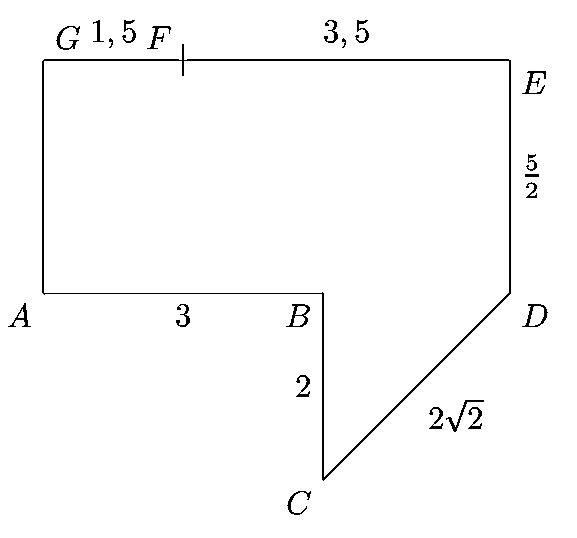
Complétez les assertions par un intervalle :
a) Si $M \in [AB]$ alors $AM \in \dots$.
b) Si $M \in [BC]$ alors $BM \in \dots$.
c) Si $M \in [CD]$ alors $CM \in \dots$.
d) Si $M \in [DE]$ alors $EM \in \dots$.
e) Si $M \in [GF]$ alors $GM \in \dots$.
f) Si $M \in [EF]$ alors $AB+BC+CD+DE+EM \in \dots$.
Exercice 10 : Ensemble des solutions d'inéquations (intervalles)
Donnez l'ensemble des solutions des inéquations sous forme d'intervalle :
a) $x<-1$
b) $3\geqslant x$
c) $\frac{1}{2} \leqslant x$
d) $-\sqrt{2}$ < $x$
e) $10^3>x$
f) $x\leqslant 2,14$
g) $x>\sqrt{\pi}$
h) $x \geqslant -2,1$
Résolution d'inéquations du premier degré
Exercice 11 : Résolution d'inéquations simples
Résolvez les inéquations suivantes :
a) $-3x+7 < x+2$
b) $-5x-2\le 0$
c) $-x> 9$
d) $-x+5\leqslant 7-6x$
e) $2(3-x)\geqslant 8$
f) $2x-7 < (3x-4)-x$
g) $3x-(4+3x) > 2$
h) $(2x-1)(2x+3)\leqslant (2x+4)^2$
Exercice 12 : Systèmes d'inéquations
Trouvez tous les nombres $x$ qui vérifient les deux inéquations dans chaque système :
a) $\left\{ \begin{array}{l} x+7 \le 12\\ x-5 \ge -17 \\ \end{array} \right.$
b) $\left\{ \begin{array}{l} 2x-8 \le 5x+13 \\ 4x-23 \le 10+x \end{array} \right.$
c) $\left\{ \begin{array}{l} 2x-8 \ge 5x +13 \\ 4x-23 \ge 10 + x \end{array} \right.$
d) $\left\{ \begin{array}{l} 2x-8 \le 5x +13 \\ 4x-23 \ge 10 + x \end{array} \right.$
Exercice 13 : Domaines de définition et inéquations
1. a) Résolvez l'équation $8x-4=0$.
b) Résolvez l'inéquation $8x-4\geqslant 0$.
2. Déduisez de la question 1 les ensembles de définition des fonctions suivantes :
a) $g:x \mapsto \dfrac{1}{8x-4}$.
b) $h:x \mapsto \sqrt{8x-4}$.
Exercice 14 : Comparaison de coûts de transport
Un particulier a des marchandises à faire transporter. Un premier transporteur lui demande 460 euros au départ et 3,50 euros par kilomètre. Un second transporteur lui demande 1000 euros au départ et 2 euros par kilomètre.
Pour quelles distances à parcourir est-il plus avantageux de s'adresser au second transporteur ?
Exercice 15 : Rentabilité d'impression de livres
Une société veut imprimer des livres. La location de la machine revient à 750 euros par jour et les frais de fabrication s'élèvent à 3,75 euros par livre.
Combien faut-il imprimer de livres par jour pour que le prix de revient d'un livre soit inférieur ou égal à 6 euros ?
Exercice 16 : Encadrement d'un rationnel
On considère un nombre rationnel $\frac{p}{q}$, où $p$ et $q$ sont des nombres entiers, $q$ étant non nul. Ce nombre a pour valeur approchée par excès à $10^{- 3}$ près $1,118$. On sait de plus que $q $ = 1789.
Quelle(s) est (sont) la (les) valeur(s) possible(s) pour $p$ ?