Revoyons ensemble les points essentiels sur Fonctions : Images et Antécédents avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Définitions clés
Fonction : Une fonction $f$ est un processus qui, à chaque nombre $x$ (appelé antécédent), associe, au plus, un unique nombre $y$ (appelé image de $x$ par $f$, noté $f(x)$).
Image : L'image de $x$ par $f$ est la valeur $f(x)$ obtenue après avoir appliqué la fonction $f$ à $x$.
Antécédent : Un antécédent de $y$ par $f$ est un nombre $x$ tel que $f(x) = y$. Un nombre peut avoir zéro, un ou plusieurs antécédents par une fonction.
2. Représentations graphiques
Courbe représentative : L'ensemble des points de coordonnées $(x, f(x))$ forme la courbe représentative de la fonction $f$.
Lecture graphique de l'image : Pour trouver l'image de $x_0$, on cherche le point de la courbe d'abscisse $x_0$. Son ordonnée est $f(x_0)$.
Lecture graphique des antécédents : Pour trouver les antécédents de $y_0$, on cherche les points de la courbe d'ordonnée $y_0$. Leurs abscisses sont les antécédents de $y_0$.
3. Calculs d'images et d'antécédents
Calcul de l'image : Pour calculer l'image de $x$, on remplace $x$ par sa valeur dans l'expression de $f(x)$.
Calcul des antécédents : Pour trouver les antécédents de $y$, on doit résoudre l'équation $f(x) = y$. La résolution de cette équation dépend de la forme de la fonction $f$.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Fonctions : Images et Antécédents
Exercice 1: lire image et antécédent graphiquement - Troisième seconde
$f$ est la fonction définie par ce graphique:
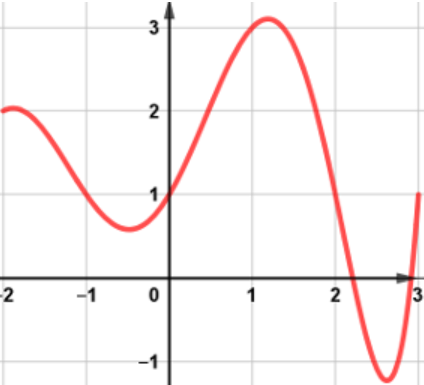
1. Lire $f(1)$ et $f(0)$.
2.Lire l'image de 3 par $f$.3. Lire le(s) antécédent(s) de 1 par $f$.
4. Combien $0$ a-t-il d'antécédent par $f$?
Exercice 2: Traduire image antécédent - Troisième Seconde
| Notation mathématique | En français |
|---|---|
| $f(5)=3$ | L'image de ..... est ....... |
| $f(1)=-2$ | Un antécédent de ..... est ...... |
| $f(....)=....$ | $4$ est l'image de $-5$. |
| $f(....)=....$ | $2$ a pour antécédent $8$. |
| $f(....)=....$ | La courbe de $f$ passe par le point $\rm A(7;-1)$. |
Exercice 3: Traduire à l'aide d'image et antécédents - troisième seconde
- Traduire chaque phrase par une égalité du type $f(\dots) = \dots$.
- $12$ est l'image de $5$ par la fonction $f$.
- $-2$ a pour image $8,5$ par la fonction $f$.
- $\dfrac{1}{2}$ a pour antécédent $0$ par la fonction $f$.
- Un antécédent de $4$ est $1$ par la fonction $f$.
- Construire quatre phrases en prenant pour modèle la question précédente pour traduire que $f(7) = 11$.
Exercice 4: Déterminer image et antécédent par le calcul à l'aide de f(x)=.... - troisième seconde
- Recopier et compléter : $f(x) = \dots \dots $
-
Est-il vrai que :
- L'image de $-3$ est $0$ ?
- $70$ a pour antécédent $7$ ?
- $2$ a pour image $7$ ?
- $-4$ est un antécédent de $4$ ?
Exercice 5: Fonction et tableau de valeur - troisième seconde
| $x$ | $-3$ | $-2$ | $-1$ | $2$ | $5$ | $10$ |
|---|---|---|---|---|---|---|
| $f(x)$ | $10$ | $5$ | $2$ | $-2$ | $10$ | $-1$ |
- Donner l'image de $2$ puis de $-2$ puis de $5$.
- Donner un antécédent de $2$ puis $-2$ puis $5$.
- Léa affirme : "$f(-1) = 10$". A-t-elle raison ? Si non, expliquer son erreur.
- On recherche les nombres $a$ tels que $f(a) = 10$. Indiquer les valeurs possibles.
Exercice 7: Traduire image et antécédent - fonction Troisième seconde
$f$ désigne une fonction. Traduire en français l'égalité $f(-1)=8$ de 5 façons différentes:
• avec le mot image et le verbe être.
• avec le mot antécédent et le verbe avoir.
• avec le mot antécédent et le verbe être.
• avec le mot courbe.
Exercice 8: Ne PLUS confondre image et antécédent - Troisième Seconde
Soit $g$ la fonction définie par $g(x)=-7x-5$.
- Antoine affirme : "Un antécédent de $-3$ est $16$ par $g$".
- Lætitia répond: "Mais non, $16$ a pour image $-3$ par $g$".
- Lotfi ajoute: "Vous vous trompez tous les deux, $16$ a pour antécédent $-3$ par $g$".
Exercice 9: Image - antécédent par le calcul - Troisième Seconde
Soit $f$ la fonction définie par $f(x)=3x+5$. Les affirmations suivantes sont-elles vraies ou fausses?
• -1 est l'image de 2.
• Un antécédent de 1 est 8.
• -3 a pour antécédent -4.
Exercice 10: Fonction trajectoire d'une balle
On lance une balle en l'air. On note $h(t)$ la hauteur de la balle en mètres au-dessus du sol au
bout de $t$ secondes de trajet en l'air avec $t$ compris entre 0 et 3.
On a tracé ci-dessous la courbe représentative de la fonction $h$:
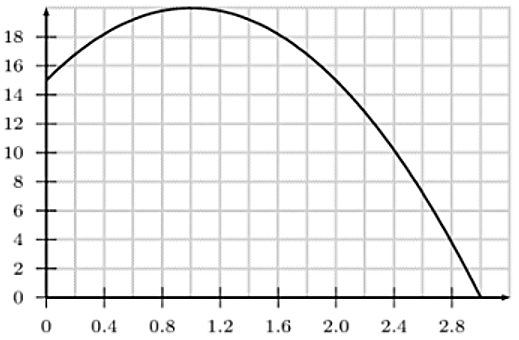
- Déterminer graphiquement $h(2,4)$. Interpréter.
- Déterminer graphiquement l'image de $0$ par la fonction $h$. Interpréter.
- Déterminer graphiquement le ou les antécédent(s) de $18$ par la fonction $h$. Interpréter
- Pour quelle valeur de $t$ a-t-on $h(t) = 0$ ? Interpréter.
Exercice 12: Déterminer l'expression de $f(x)$ en fonction de $x$ - troisième seconde
- $f$ est la fonction qui, au côté $x$ en cm d'un triangle équilatéral, associe son périmètre en cm.
- $g$ est la fonction qui, au rayon $x$ en cm d'un disque, associe son aire en cm$^2$.
- $h$ est la fonction qui, à la quantité $x$ en kg de pommes achetée, associe son prix en euro sachant que le kg de pommes coûte $1,50$ €.
- $v$ est la fonction qui, au côté $x$ en cm d'un cube, associe son volume en cm$^3$.
Exercice 13: Déterminer image et antécédent par le calcul à l'aide de f(x)=.... - troisième seconde
- Calculer l'image de $4$.
- Calculer $f(-3)$.
- Vérifier que $-1$ et $3$ sont des antécédents d'un même nombre.