Revoyons ensemble les points essentiels sur les Fonctions Affines avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Définition et Forme
Définition : Une fonction affine est une fonction de la forme $f(x) = ax + b$, où $a$ et $b$ sont des nombres réels constants.
Coefficient directeur ($a$) : Le coefficient $a$ détermine la pente de la droite représentative et indique la variation de $y$ lorsque $x$ augmente d'une unité.
Ordonnée à l'origine ($b$) : L'ordonnée à l'origine $b$ est la valeur de $f(x)$ lorsque $x = 0$. Graphiquement, c'est l'ordonnée du point d'intersection de la droite avec l'axe des ordonnées.
2. Représentation Graphique
Droite : La représentation graphique d'une fonction affine est toujours une droite.
Tracé : Pour tracer une droite, deux points suffisent. On peut calculer les images de deux valeurs de $x$ et placer les points correspondants dans un repère.
Coefficient directeur et pente : Le coefficient directeur $a$ représente la pente de la droite. Si $a > 0$, la droite monte ; si $a < 0$, la droite descend ; si $a = 0$, la droite est horizontale (fonction constante).
3. Variations et Signe
Variations :
- Si $a > 0$, la fonction affine est strictement croissante.
- Si $a < 0$, la fonction affine est strictement décroissante.
- Si $a = 0$, la fonction affine est constante.
Tableau de signes : Pour étudier le signe d'une fonction affine, on recherche sa racine (valeur de $x$ qui annule la fonction) et on utilise le signe du coefficient directeur pour déterminer le signe avant et après la racine.
4. Détermination de l'expression
À partir de deux points : Si on connaît les coordonnées de deux points $(x_1, y_1)$ et $(x_2, y_2)$ appartenant à la droite, on peut déterminer le coefficient directeur $a = \frac{y_2 - y_1}{x_2 - x_1}$ puis l'ordonnée à l'origine $b$ en utilisant l'équation $y_1 = ax_1 + b$ (ou $y_2 = ax_2 + b$).
Système d'équations : La détermination de l'expression d'une fonction affine à partir de deux points revient à résoudre un système de deux équations linéaires à deux inconnues ($a$ et $b$).
5. Intersection de droites
Point d'intersection : Le point d'intersection de deux droites (représentant deux fonctions affines) est le point dont les coordonnées $(x; y)$ vérifient simultanément les équations des deux droites.
Calcul des coordonnées : Pour trouver les coordonnées du point d'intersection, on résout le système d'équations formé par les équations des deux droites. On peut utiliser la méthode par substitution ou par combinaison linéaire.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
1. Identification de fonctions affines
Exercice 1 : Identifier si les fonctions sont affines
Pour chacune des fonctions suivantes, déterminez si elle est affine. Si oui, précisez son coefficient directeur (a) et son ordonnée à l'origine (b).
$f_1(x) = 3x - 7$
$f_2(x) = -2x + \frac{1}{2}$
$f_3(x) = 5$
$f_4(x) = x^2 + 1$
$f_5(x) = \frac{1}{x} + 2$
$f_6(x) = \sqrt{2}x - \pi$
Exercice 2 : Identifier si les fonctions sont affines
Pour chacune des fonctions suivantes, déterminez si elle est affine. Si oui, précisez son coefficient directeur (a) et son ordonnée à l'origine (b).
$f_7(x) = -x + 4$
$f_8(x) = \frac{3}{2}x -1$
$f_9(x) = \frac{1}{4} - x$
$f_{10}(x) = 2(x+1) - 2x$
$f_{11}(x) = x^3 - 1$
$f_{12}(x) = 4 - \sqrt{3}x$
Exercice 3 : Identifier si les fonctions sont affines
Pour chacune des fonctions suivantes, déterminez si elle est affine. Si oui, précisez son coefficient directeur (a) et son ordonnée à l'origine (b).
$f_{13}(x) = 5(x-2) + 6$
$f_{14}(x) = \sqrt{x} + 1$
$f_{15}(x) = \frac{5}{x} - 4$
$f_{16}(x) = \frac{2x - 1}{4}$
$f_{17}(x) = 3x$
$f_{18}(x) = -1$
2. Variations des fonctions affines
Exercice 4 : Déterminer les variations des fonctions affines
Déterminez si les fonctions affines suivantes sont croissantes, décroissantes ou constantes.
$g_1(x) = 4x - 1$
$g_2(x) = -x + 5$
$g_3(x) = 2$
$g_4(x) = -\frac{1}{3}x - 2$
Exercice 5 : Déterminer les variations des fonctions affines
Déterminez si les fonctions affines suivantes sont croissantes, décroissantes ou constantes.
$g_5(x) = -2x + 7$
$g_6(x) = \frac{1}{2}x - 3$
$g_7(x) = -0.5$
$g_8(x) = 4 - x$
Exercice 6 : Déterminer les variations des fonctions affines
Déterminez si les fonctions affines suivantes sont croissantes, décroissantes ou constantes.
$g_9(x) = 3(x-1) + 2$
$g_{10}(x) = -2(x+4) - 1$
$g_{11}(x) = \frac{3x-1}{2} + 4$
$g_{12}(x) = 5 - \frac{x}{3}$
Exercice 7 : Déterminer les variations des fonctions affines
Déterminez si les fonctions affines suivantes sont croissantes, décroissantes ou constantes.
$g_{13}(x) = 7 - 4x$
$g_{14}(x) = \frac{5-2x}{3}$
$g_{15}(x) = \frac{x}{2} + \frac{1}{4}$
$g_{16}(x) = -1$
3. Représentation graphique
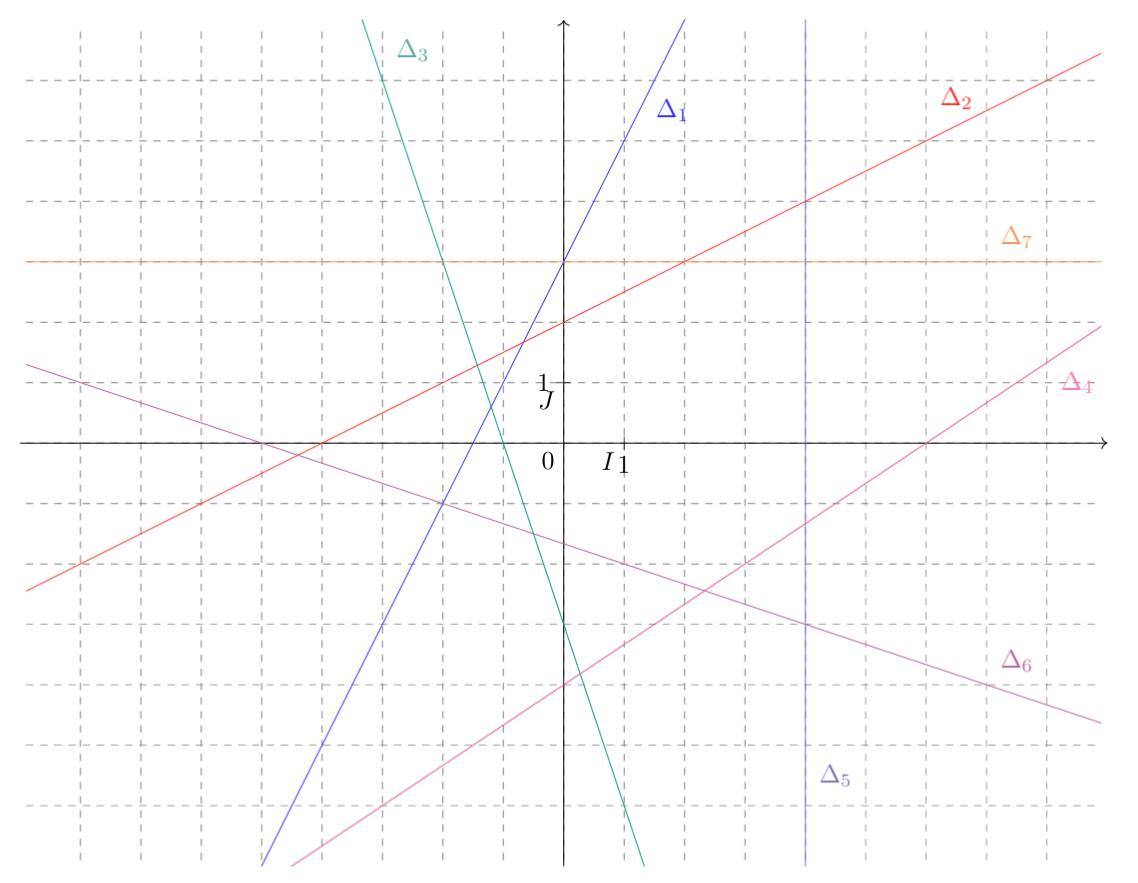
Exercice 8 : Déterminer l'expression des fonctions affines à partir de leur représentation graphique
Le graphique suivant montre les représentations graphiques de plusieurs fonctions affines, notées $\Delta_1$ à $\Delta_7$. Déterminez l'expression de chacune de ces fonctions.
Exercice 9 : Tracer la représentation graphique d'une fonction affine
Tracez la représentation graphique de la fonction affine $f(x) = 2x - 3$ dans un repère orthonormé.
Exercice 10 : Tracer la représentation graphique d'une fonction affine
Tracez la représentation graphique de la fonction affine $g(x) = -x + 4$ dans un repère orthonormé.
Exercice 11 : Tracer la représentation graphique d'une fonction affine
Tracez la représentation graphique de la fonction affine $h(x) = \frac{1}{2}x - 2$ dans un repère orthonormé.
4. Tableaux de signes
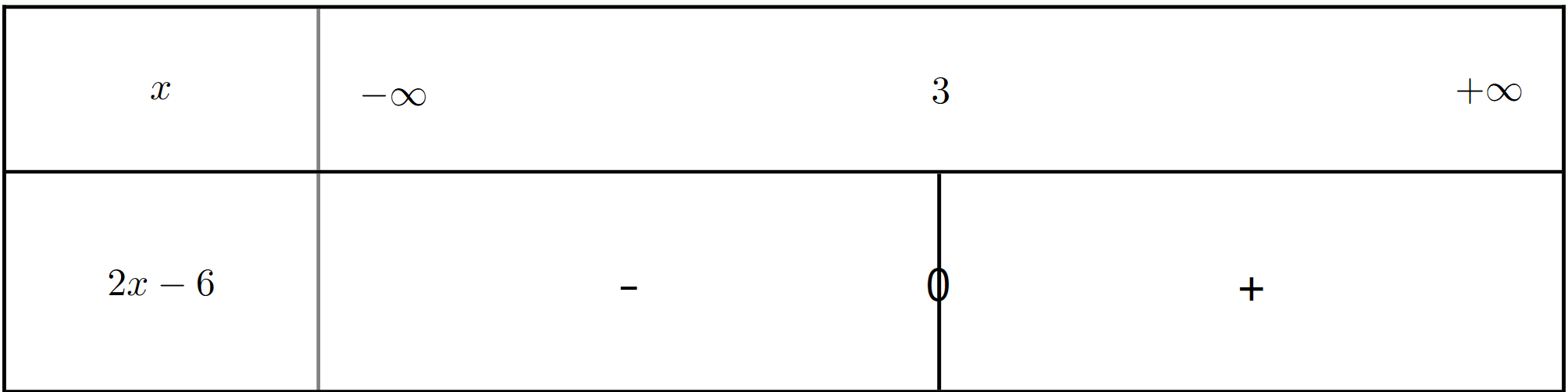
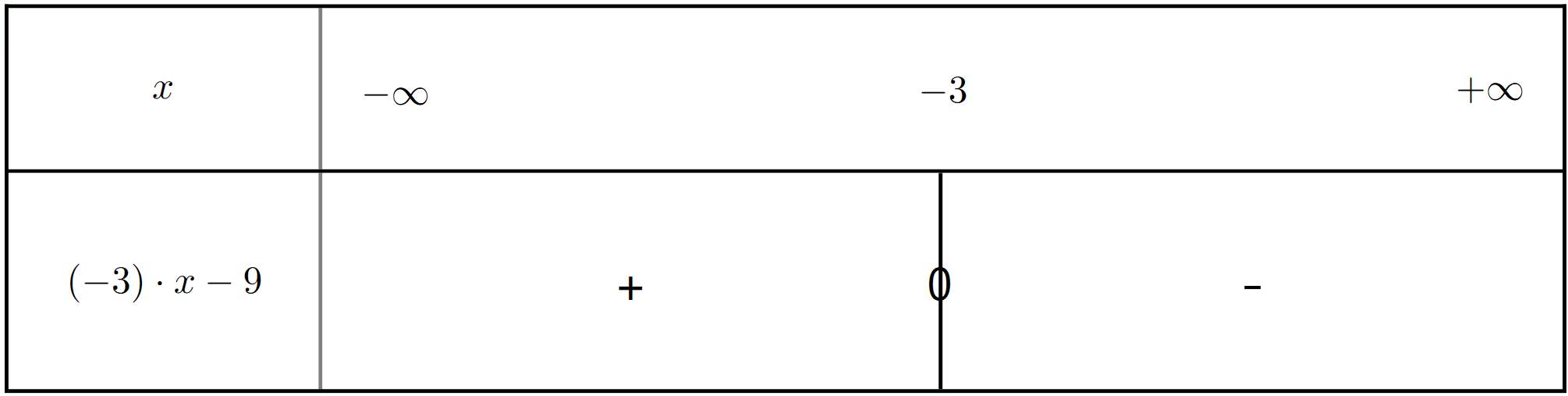
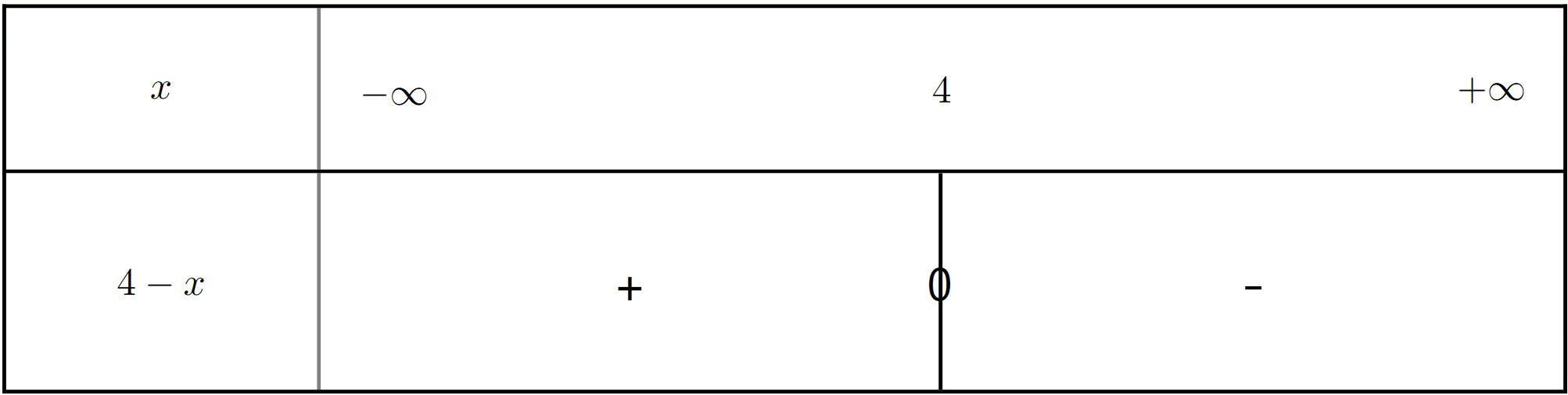
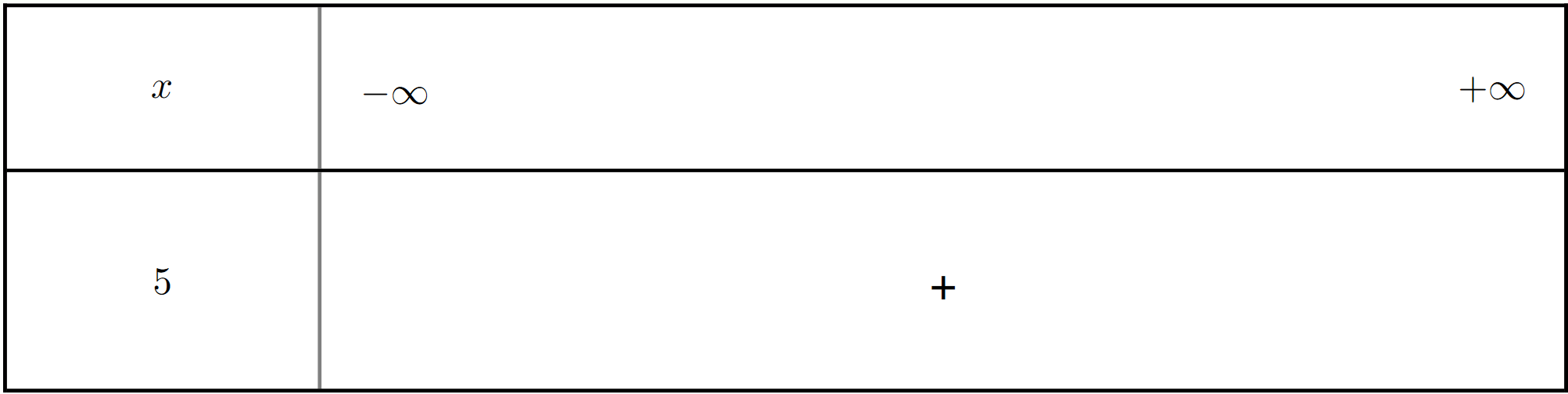
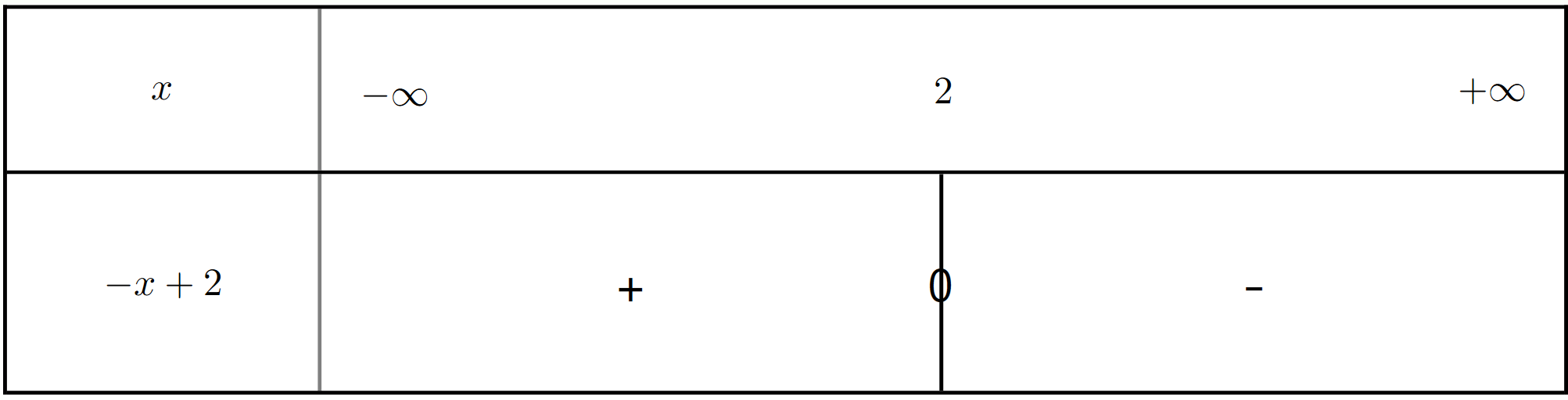
Exercice 12 : Créer les tableaux de signes des fonctions affines
Créez les tableaux de signes pour les fonctions affines suivantes :
$h_1(x) = 2x - 6$
$h_2(x) = -3x - 9$
$h_3(x) = 4 - x$
$h_4(x) = 5$
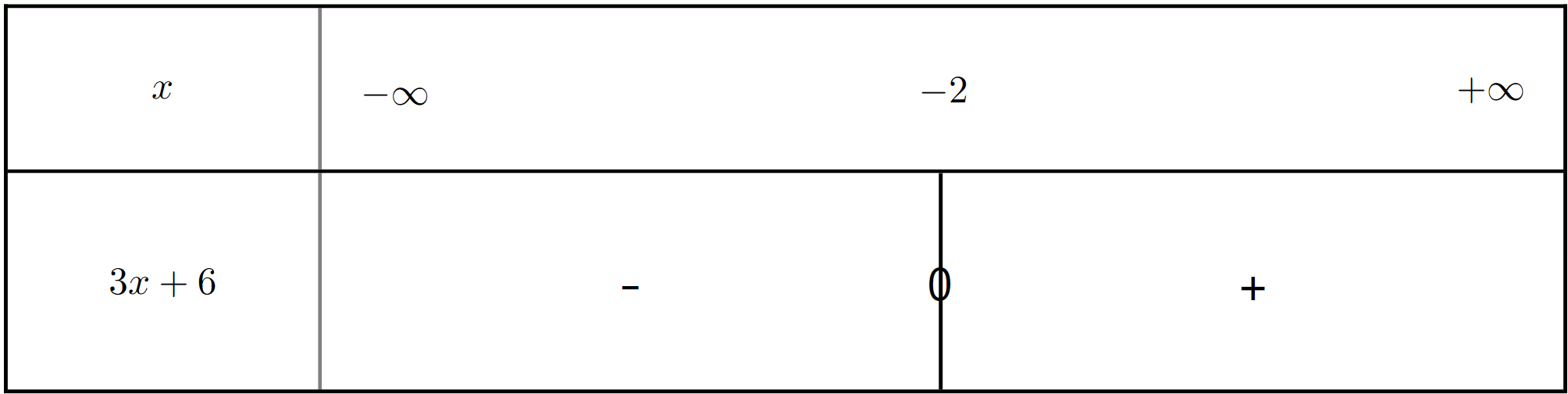
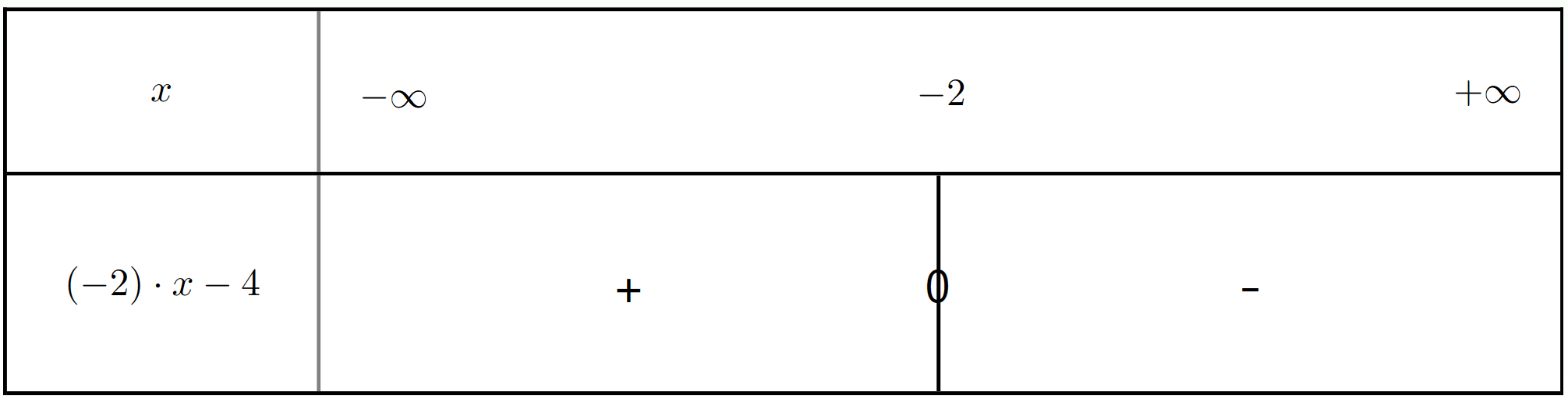
Exercice 13 : Créer les tableaux de signes des fonctions affines
Créez les tableaux de signes pour les fonctions affines suivantes :
$h_5(x) = -x + 2$
$h_6(x) = 3x + 6$
$h_7(x) = -2x - 4$
$h_8(x) = -3$
5. Recherche de fonctions connaissant les images
Exercice 14 : Déterminer l'expression d'une fonction affine à partir de deux points
Déterminez l'expression de la fonction affine $k(x)$ sachant que $k(2) = 1$ et $k(-1) = 3$.
Exercice 15 : Déterminer l'expression d'une fonction affine à partir de deux points
Déterminez l'expression de la fonction affine $m(x)$ sachant que $m(-2) = 5$ et $m(3) = -5$.
Exercice 16 : Déterminer l'expression d'une fonction affine à partir de deux points
Déterminez l'expression de la fonction affine $n(x)$ sachant que $n(1) = 4$ et $n(3) = 0$.
6. Intersection de fonctions affines
Exercice 17 : Trouver les coordonnées du point d'intersection de deux fonctions affines
Trouvez les coordonnées du point d'intersection des droites représentant les fonctions $p(x) = 2x - 3$ et $q(x) = -x + 6$.
Exercice 18 : Trouver les coordonnées du point d'intersection de deux fonctions affines
Trouvez les coordonnées du point d'intersection des droites représentant les fonctions $r(x) = 3x + 1$ et $s(x) = -2x + 6$.
Exercice 19 : Trouver les coordonnées du point d'intersection de deux fonctions affines
Trouvez les coordonnées du point d'intersection des droites représentant les fonctions $t(x) = -x + 4$ et $u(x) = 2x - 5$.
7. Problèmes divers
Exercice 20 : Modélisation du coût d'un trajet en taxi
Un taxi facture un prix de base de 4€ plus 2€ par kilomètre parcouru.
a) Exprimez le coût total $C(x)$ d'une course en taxi en fonction de la distance $x$ en kilomètres.
b) Quel est le coût d'une course de 15 km ?
c) Si une course coûte 30€, quelle distance a été parcourue ?
Exercice 21 : Modélisation du coût d'impression
Une imprimerie propose un tarif dégressif pour les photocopies. Le prix unitaire est de 0,10€ pour les 20 premières photocopies et de 0,08€ pour les suivantes.
a) Exprimez le coût total $P(x)$ de $x$ photocopies en fonction de $x$.
b) Quel est le coût de 15 photocopies ?
c) Quel est le coût de 30 photocopies ?
d) Si on a payé 4,40€, combien de photocopies a-t-on faites ?
Exercice 22 : Fonction affine et partage d'argent
Trois frères, Alex, Benjamin et Charles, se partagent une somme d'argent. Alex reçoit le double de la part de Benjamin, et Charles reçoit 10€ de moins que Benjamin. On note $x$ la part de Benjamin.
a) Exprimez la part d'Alex, notée $A(x)$, en fonction de $x$.
b) Exprimez la part de Charles, notée $C(x)$, en fonction de $x$.
c) Exprimez la somme totale, notée $S(x)$, en fonction de $x$.
d) Si la somme totale à partager est de 150€, quelle est la part de chacun ?
Exercice 23 : Fonction affine et modélisation de la vitesse
Un train parcourt une distance de 300 km à une vitesse constante.
a) Exprimez le temps de trajet $t(v)$ (en heures) en fonction de la vitesse $v$ (en km/h).
b) Si le train roule à 150 km/h, quel sera le temps de trajet ?
c) Si le temps de trajet est de 4 heures, quelle était la vitesse du train ?
d) La fonction $t(v)$ est-elle une fonction affine ?
Exercice 24 : Fonction affine et évolution de population
La population d'une ville augmente de 2% par an. En 2020, la population était de 50 000 habitants.
a) Exprimez la population $P(n)$ en fonction du nombre d'années $n$ écoulées depuis 2020.
b) Quelle sera la population en 2025 ?
c) En quelle année la population atteindra-t-elle 60 000 habitants ? (On arrondira à l'année près.)
d) La fonction $P(n)$ est-elle une fonction affine ?
Exercice 25 : Fonction affine et mélange de solutions
On dispose de deux solutions d'acide chlorhydrique, l'une à 25% et l'autre à 50%. On veut obtenir 10 litres d'une solution à 40%.
a) Soit $x$ le nombre de litres de la solution à 25% utilisés. Exprimez en fonction de $x$ la quantité d'acide chlorhydrique pur dans la solution finale.
b) Quelle quantité de chaque solution doit-on utiliser ?
Exercice 26 : Fonction affine et modélisation de l'offre et de la demande
Sur un marché, l'offre et la demande d'un produit sont modélisées par les fonctions affines suivantes :
Offre : $O(p) = 2p - 10$
Demande : $D(p) = -3p + 80$
où $p$ est le prix unitaire du produit en euros, $O(p)$ est la quantité offerte et $D(p)$ est la quantité demandée.
a) Déterminer le prix d'équilibre du marché, c'est-à-dire le prix pour lequel l'offre est égale à la demande.
b) Quelle est la quantité offerte et demandée à ce prix ?
c) Si le prix est fixé à 20 euros, y a-t-il un excédent d'offre ou de demande ? De quelle quantité ?
Exercice 27 : Fonction affine et optimisation de la production
Une entreprise fabrique des jouets. Le coût de production de $x$ jouets est donné par $C(x) = 5x + 100$ (en euros) et chaque jouet est vendu 15 euros.
a) Exprimer le bénéfice $B(x)$ réalisé par la vente de $x$ jouets.
b) Combien de jouets l'entreprise doit-elle vendre pour réaliser un bénéfice de 500 euros ?
c) L'entreprise peut-elle réaliser un bénéfice de 1000 euros en produisant 80 jouets ?
Exercice 28 : Fonction affine et modélisation de l'évaporation
Un réservoir d'eau de 1000 litres se vide par évaporation. Chaque jour, le réservoir perd 2% de son volume.
a) Exprimer le volume d'eau $V(n)$ restant dans le réservoir après $n$ jours en fonction de $n$.
b) Quel sera le volume d'eau restant après 10 jours ?
c) Après combien de jours le volume d'eau sera-t-il inférieur à 500 litres ?
d) La fonction $V(n)$ est-elle une fonction affine ?
Exercice 29 : Fonction affine et partage proportionnel
Un héritage de 100 000 euros doit être partagé entre trois personnes proportionnellement à leur âge. Les âges des trois personnes sont 20, 30 et 50 ans.
a) Modéliser la part de chaque personne en fonction de son âge par une fonction affine.
b) Quelle sera la part de chaque personne ?
Exercice 30 : Fonction affine et coût de location
Une agence de location de voitures propose deux formules :
- Formule A : un forfait de 50 euros plus 0,20 euro par kilomètre parcouru.
- Formule B : un forfait de 80 euros plus 0,10 euro par kilomètre parcouru.
a) Exprimer le coût de location $A(x)$ pour la formule A en fonction du nombre de kilomètres parcourus $x$.
b) Exprimer le coût de location $B(x)$ pour la formule B en fonction du nombre de kilomètres parcourus $x$.
c) À partir de combien de kilomètres la formule B devient-elle plus avantageuse que la formule A ?
Exercice 31 : Fonction affine et point d'intersection (3)
Déterminer les coordonnées du point d'intersection des droites d'équations $y = 4x - 7$ et $y = -2x + 5$.
Exercice 32 : Fonction affine et point d'intersection (4)
Déterminer les coordonnées du point d'intersection des droites d'équations $y = -3x + 2$ et $y = 2x - 3$.
Exercice 33 : Équation de droite
Déterminer l'équation de la droite passant par les points $A(2, -1)$ et $B(4, 3)$.
Exercice 34 : Fonction affine et distance
Une voiture se déplace à une vitesse constante de 80 km/h.
a) Exprimer la distance parcourue $d(t)$ (en km) en fonction du temps $t$ (en heures).
b) Quelle distance la voiture parcourt-elle en 2h30 ?
c) Combien de temps faut-il à la voiture pour parcourir 200 km ?
Exercice 35 : Fonction affine et évolution de prix
Le prix d'un produit subit une augmentation de 5% par an. En 2023, le prix du produit est de 120 euros.
a) Modéliser le prix $P(n)$ du produit en fonction du nombre d'années $n$ écoulées depuis 2023.
b) Quel sera le prix du produit en 2025 ?
c) En quelle année le prix du produit dépassera-t-il 150 euros ?
Exercice 36 : Fonction affine et optimisation
Un artisan fabrique des objets. Le coût de production de $x$ objets est donné par $C(x) = 4x + 80$ (en euros). Chaque objet est vendu 10 euros.
a) Exprimer le bénéfice $B(x)$ réalisé par la vente de $x$ objets.
b) Combien d'objets l'artisan doit-il vendre pour réaliser un bénéfice de 200 euros ?
c) L'artisan souhaite réaliser un bénéfice maximal en produisant au plus 50 objets. Combien d'objets doit-il produire et quel sera son bénéfice maximal ?
Exercice 37 : Fonction affine et aire
On considère un carré de côté $x$ cm. On augmente la longueur de ce carré de 3 cm et on diminue sa largeur de 1 cm.
a) Exprimer l'aire $A(x)$ du nouveau rectangle en fonction de $x$.
b) Pour quelle valeur de $x$ l'aire du nouveau rectangle est-elle égale à 30 cm² ?
c) L'aire du nouveau rectangle peut-elle être nulle ? Justifier.
Exercice 38 : Fonction affine et échelle de température
En plus des échelles Celsius et Fahrenheit, il existe l'échelle Kelvin (K). La température en Kelvin est donnée par $K = C + 273,15$, où $C$ est la température en degrés Celsius.
a) Exprimer la température en degrés Celsius en fonction de la température en Kelvin.
b) Quel est le zéro absolu (0 K) en degrés Celsius ?
c) Convertir 25°C en Kelvin.
d) Convertir 300 K en degrés Celsius.
Exercice 39 : Fonction affine et volume d'un cube
On considère un cube dont l'arête mesure $x$ cm.
a) Exprimer l'aire totale des faces du cube, $A(x)$, en fonction de $x$.
b) Exprimer le volume du cube, $V(x)$, en fonction de $x$.
c) Si l'arête du cube est augmentée de 2 cm, de combien augmente son volume ?
Exercice 40 : Fonction affine et point fixe
Soit la fonction $f(x) = -2x + 5$.
a) Déterminer s'il existe un point fixe pour la fonction $f$, c'est-à-dire un nombre $x$ tel que $f(x) = x$.
b) Interpréter graphiquement le résultat.
Exercice 41 : Conversion Celsius Fahrenheit
En France, l’unité usuelle de température est le degré Celsius, qui est noté °C. Dans certains pays anglo-saxons, comme les États-Unis, l’unité usuelle est le degré Fahrenheit, qui est noté °F. Tous les Français en visite à Los Angeles ont éprouvé un certain malaise en écoutant la météo annoncer une température de 90° pour le lendemain. Il s’agit bien évidemment de degré Fahrenheit. Réduisons ce malaise en convertissant les degrés Celsius en degré Fahrenheit à l’aide d’une fonction affine. Il faut deux informations pour déterminer cette fonction. Les changements d’états de l’eau (qui servent de base à la définition du degré Celsius), permettent la conversion :
• Quand l’eau gèle (0°C), un Californien pense 32°F.
• Quand l’eau bout (100°C), un Californien pense 212°F.
1. Déduire de ces renseignements l’expression de $f$ qui associe à une température $x$ exprimée en degré Celsius, sa valeur $f(x)$ exprimée en degré Fahrenheit.
2. a. Lorsqu’à Los Angeles, le thermomètre indique 90°F, quelle est la température en °C?
2. b. Un médecin américain s’inquiète-t-il quand le thermomètre d'un malade indique 100°F?
2. c. À quelle température en degré Fahrenheit, un touriste qui souhaite avoir sa chambre d’hôtel à une température de 24°C, doit-il régler sa climatisation?
3. Existe-t-il une température qui s’exprime par le même nombre en °C et en °F?
Exercice 42 : Aires de triangles dans un trapèze
ABCD est un trapèze rectangle tel que AB = 8, AD = 6 et DC = 2. M est un point du segment [AD] et on pose AM = $x$. On a découpé le trapèze en trois triangles $T_1$, $T_2$ et $T_3$ comme l’indique la figure. On note $f_1$, $f_2$ et $f_3$ les fonctions qui associent à $x$ les aires respectives de $T_1$, $T_2$ et $T_3$.
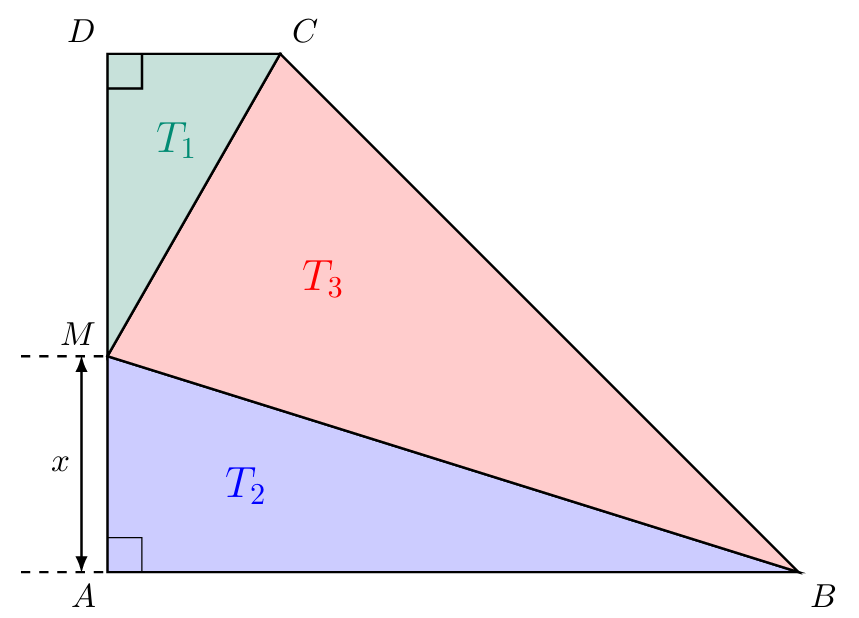
1. a. Donner une expression des fonctions $f_1$, $f_2$ et $f_3$ en fonction de $x$.
1. b. Construire dans un même repère les courbes représentatives de $f_1$, $f_2$ et $f_3$.
2. Colorier sur l’axe des abscisses l’intervalle J décrit par $x$ pour lequel : $A_{T_1} < A_{T_2} < A_{T_3}$
3. Par le calcul, préciser l’intervalle J.