Revoyons ensemble les points essentiels sur la Lecture Graphique de Fonctions avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Lecture de l'image d'un nombre ($f(x)$)
Pour lire $f(2)$, on se place sur l'axe des abscisses à la valeur $x=2$ et on monte ou descend verticalement jusqu'à rencontrer la courbe représentative de la fonction $f$. Ensuite, on lit l'ordonnée du point d'intersection sur l'axe des ordonnées.
2. Résolution graphique des équations du type $f(x)=k$
Pour résoudre graphiquement l'équation $f(x) = 2$, on trace la droite horizontale d'équation $y=2$. Les solutions de l'équation sont les abscisses des points d'intersection de cette droite avec la courbe de $f$.
3. Résolution graphique des inéquations du type $f(x)< k$
On cherche les valeurs de $x$ pour lesquelles la courbe de $f$ est au-dessus ou sur la droite horizontale d'équation $y=1$. On identifie les intervalles de l'axe des abscisses correspondants.
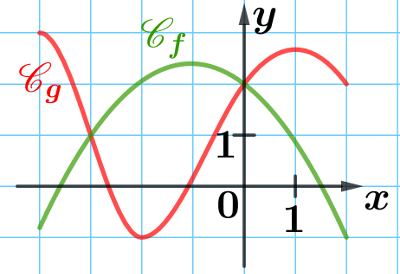
4. Résolution graphique d'équations du type $f(x)=g(x)$
Pour résoudre graphiquement l'équation $f(x) = g(x)$, on cherche les abscisses des points d'intersection des courbes $\mathscr{C}_f$ et $\mathscr{C}_g$.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Lecture Graphique
Exercice 1 : Fonction lecture graphique équation du type f(x)=k
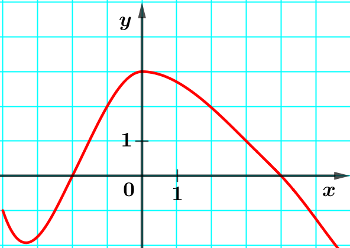
On a représenté ci-dessous la courbe d'une fonction $f$ définie sur $[-4;6]$:
- Lire $f(2)$
-
Résoudre graphiquement les équations suivantes:
a. $f(x)=2$ b. $f(x)=-1$ c. $f(x)=-2$
Exercice 2 : Lecture graphique - résoudre des équations du type $f(x)=k$
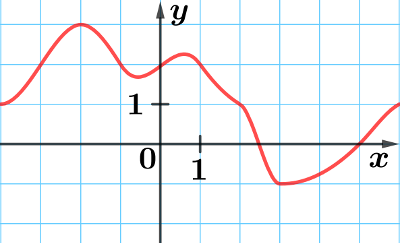
On a représenté ci-dessous la courbe d'une fonction $f$ définie sur $[-4~;~6]$:
- Lire $f(0)$.
-
Résoudre graphiquement les équations suivantes :
a. $f(x) = 0$ b. $f(x) = 1$
- Combien l'équation $f(x) = -1$ a-t-elle de solutions ?
Exercice 3 : Fonction lecture graphique inéquation du type f(x)< k
On a représenté ci-dessous la courbe d'une fonction $f$ définie sur $[-4;6]$:
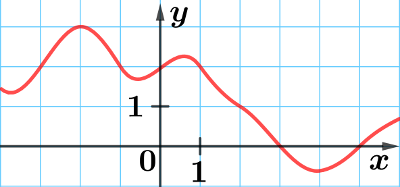
Exercice 4 : résoudre graphiquement une équation du type $f(x)=g(x)$
$\mathscr{C}_f$ et $\mathscr{C}_g$ sont les courbes représentatives de deux fonctions $f$ et $g$ définies sur $[-4;2]$: