Suites Géométriques
Révisions et exercices sur les suites géométriques pour la Première Spécialité Maths.
Revoyons ensemble les points essentiels sur les suites géométriques avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Définition d'une suite géométrique
Une suite $(u_n)$ est dite géométrique si chaque terme se déduit du précédent en multipliant par une constante appelée raison, notée $q$.
La relation de récurrence s'écrit :
$$u_{n+1} = q \times u_n$$
où $q$ est un nombre réel constant.
2. Terme général d'une suite géométrique
Si $(u_n)$ est une suite géométrique de raison $q$ et de premier terme $u_0$, alors le terme général $u_n$ est donné par :
$$u_n = u_0 \times q^n$$
Plus généralement, si le premier terme est $u_p$, alors :
$$u_n = u_p \times q^{n-p}$$
En particulier, si on connaît $u_1$ comme premier terme, alors :
$$u_n = u_1 \times q^{n-1} \text{ pour } n \geqslant 1$$
3. Sens de variation d'une suite géométrique
Le sens de variation d'une suite géométrique $(u_n)$ dépend du signe de son premier terme $u_0$ et de la valeur de sa raison $q$.
Cas où $u_0 > 0$ :
- Si $q > 1$, alors la suite $(u_n)$ est strictement croissante.
- Si $q = 1$, alors la suite $(u_n)$ est constante.
- Si $0 < q < 1$, alors la suite $(u_n)$ est strictement décroissante.
- Si $q \leqslant 0$, la suite n'est pas monotone (elle alterne entre croissance et décroissance ou termes positifs et négatifs).
Cas où $u_0 < 0$ :
- Si $q > 1$, alors la suite $(u_n)$ est strictement décroissante.
- Si $q = 1$, alors la suite $(u_n)$ est constante.
- Si $0 < q < 1$, alors la suite $(u_n)$ est strictement croissante.
- Si $q \leqslant 0$, la suite n'est pas monotone.
Cas où $u_0 = 0$ :
Si $u_0 = 0$, alors tous les termes de la suite sont nuls, et la suite est constante et nulle.
4. Représentation graphique
La représentation graphique d'une suite géométrique est un ensemble de points isolés dont les ordonnées forment une progression géométrique. Sur un graphique, on place les points de coordonnées $(n, u_n)$.
Pour une suite géométrique de raison $q > 0$, les points sont alignés si on utilise une échelle logarithmique sur l'axe des ordonnées.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
$(u_n)$ est une suite géométrique de raison $q$. Dans chaque cas, déterminer $u_1$, $u_2$ et $u_3$:
Exercice 2
$(u_n)$ est une suite géométrique de raison $5$. On sait que $u_2=10$. Déterminer $u_3$, $u_1$ et $u_0$.
Exercice 3
On a représenté une suite géométrique $(u_n)$:
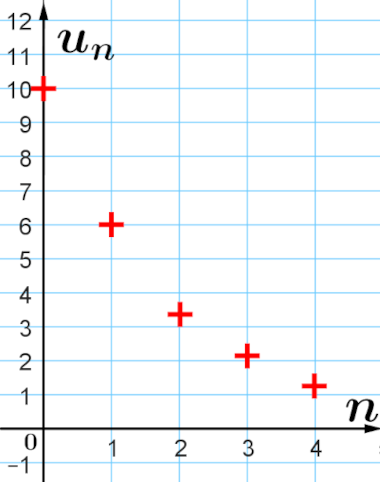
- Lire $u_0$ et la raison $q$.
- Donner l'expression de $u_n$ en fonction de $n$.
Exercice 4
Dans chaque cas, donner l'expression $u_n$ en fonction de $n$:
- $(u_n)$ est une suite géométrique de raison $5$ et $u_0=2$.
- Pour tout entier $n \geqslant 0$, $u_{n+1}=3u_n$ et $u_0=4$.
Exercice 5
Déterminer le sens de variations des suites suivantes définies pour tout entier naturel $n$ par:
Exercice 6
Déterminer le sens de variations des suites suivantes définies pour tout entier naturel $n$ par:
Exercice 7
Un scientifique observe l'évolution d'une population de poissons dans un aquarium. Il compte $500$ poissons en 2019 et $600$ en 2020. Il décide de modéliser l'évolution du nombre de poissons par une suite géométrique.
- Déterminer la raison de cette suite.
- Le scientifique compte $761$ poissons en 2022. Que penser de cette modélisation?
Exercice 8
On considère la suite $(u_n)$ définie pour tout entier naturel $n$, par: $ \left\{ \begin{array}{l} u_0 = 4 \\ u_{n+1}=\dfrac{u_n}{5}+8 \end{array} \right.$
- La suite $(u_n)$ est-elle arithmétique? géométrique? Justifier.
- $(v_n)$ est la suite définie pour tout entier
naturel $n$
par $v_n=u_n-10$.
a. Démontrer que la suite $(v_n)$ est géométrique.
b. En déduire l'expression de $v_n$ puis de $u_n$ en fonction de $n$.
Exercice 9
$(u_n)$ est la suite définie par $u_0=10$ et pour tout entier naturel $n$, $u_{n+1}=0,5u_n+3$.
- Démontrer que $(u_n)$ n'est ni arithmétique, ni géométrique.
- $(v_n)$ est la suite définie pour tout entier
naturel $n$
par $v_n=u_n-6$.
- Démontrer que $(v_n)$ est géométrique.
- En déduire l'expression de $v_n$ puis de $u_n$ en fonction de $n$.
- En déduire la limite de $(u_n)$
Exercice 10
Une action est cotée à $57$€. Sa valeur augmente de $3\%$ tous les mois. Écrire une fonction en Python qui renvoie le nombre de mois à attendre pour que sa valeur dépasse $200$€.
Exercice 11
Préciser si les suites suivantes, définies sur $\mathbb{N}$, sont géométriques. Dans ce cas, indiquer alors la raison $q$ et le premier terme.
Exercice 12
Préciser si les suites suivantes, définies sur $\mathbb{N}$, sont géométriques. Dans l'affirmative, indiquer alors la raison et le premier terme:
Exercice 13
On considère les suites $u$ et $v$ telles que $u_0=1$ et pour tout entier naturel $n$,
$u_{n+1}=\dfrac12 u_n+3$ et $v_n=u_n-6$.
- La suite $(u_n)$ est-elle arithmétique? géométrique? Justifier.
- Montrer que la suite $(v_n)$ est géométrique.
- En déduire l'expression de $v_n$ puis de $u_n$ en fonction de $n$.
Exercice 14
- Est-ce que les nombres 7 ; 14 ; 21 sont les termes consécutifs d'une suite géométrique?
- Est-ce que les nombres $\dfrac13$ ; 2 ; 12 sont les termes consécutifs d'une suite géométrique?
- Est-ce que les nombres $\dfrac13$ ; $-2$ ; 12 sont les termes consécutifs d'une suite géométrique?
- Est-ce que les nombres $16$ ; $12$ et $9$ sont les termes consécutifs d'une suite géométrique?
- Déterminer $x$ pour que les nombres 7; $x$; 63 soient les termes consécutifs d'une suite géométrique.
Exercice 15
- La suite $(u_n)$ est géométrique. $u_0=-8$ et $q=\dfrac12$. Déterminer $u_{4}$.
- La suite $(v_n)$ est géométrique. $v_{1}=2$ et $v_2=-6$. Déterminer la raison et $v_{0}$.
- La suite $(t_n)$ est géométrique. $t_2=3$ et $t_4=12$. Que peut-on dire de la raison et de $t_3$?
- La suite $(w_n)$ est géométrique. $q=0.1$ et $w_{4}=2$. Déterminer $w_{0}$.
- La suite $(a_n)$ est définie par $\left\{ \begin{array}{l} a_0 = 4 \\ a_{n+1}=a_n- \dfrac{2}{3}\times a_n \end{array} \right.$ est-elle géométrique?
- La suite $(b_n)$ est géométrique de raison $4$. Exprimer $b_n$ en fonction de $b_1$.