Exercices : Suites Arithmétiques

Correction :

1. Pour la suite $(u_n)$, nous connaissons le premier terme $u_0 = 5$ et la raison $r = 3$. Par définition d'une suite arithmétique, chaque terme s'obtient en ajoutant la raison au terme précédent. Ainsi :

$u_1 = u_0 + r = 5 + 3 = 8$

$u_2 = u_1 + r = 8 + 3 = 11$

$u_3 = u_2 + r = 11 + 3 = 14$

Donc, les premiers termes de la suite $(u_n)$ sont $u_1 = 8$, $u_2 = 11$ et $u_3 = 14$.

2. Pour la suite $(v_n)$, nous connaissons la raison $r = 0,5$ et un terme $v_3 = 7$. Nous devons remonter pour trouver $v_0$, $v_1$ et $v_2$. Puisque $v_{n+1} = v_n + r$, alors $v_n = v_{n+1} - r$.

Pour trouver $v_2$, nous utilisons $v_2 = v_3 - r = 7 - 0,5 = 6,5$

Pour trouver $v_1$, nous utilisons $v_1 = v_2 - r = 6,5 - 0,5 = 6$

Pour trouver $v_0$, nous utilisons $v_0 = v_1 - r = 6 - 0,5 = 5,5$

Ainsi, les premiers termes de la suite $(v_n)$ sont $v_0 = 5,5$, $v_1 = 6$ et $v_2 = 6,5$.

Conclusion : Pour calculer les termes d'une suite arithmétique, on utilise la relation de récurrence $u_{n+1} = u_n + r$ dans le sens direct pour avancer dans la suite, et dans le sens inverse $u_n = u_{n+1} - r$ pour remonter.

Correction :

Pour déterminer le terme général $u_n$ d'une suite arithmétique, on utilise la formule explicite :

$$u_n = u_p + (n-p)r$$

où $u_p$ est un terme connu de la suite et $r$ est la raison.

a. Cas où $u_0 = -10$ et $r = 4$ :

Ici, le premier terme connu est $u_0$, donc on utilise $p=0$. La formule devient :

$$u_n = u_0 + (n-0)r = u_0 + nr$$

En remplaçant $u_0$ et $r$ par leurs valeurs, on obtient :

$$u_n = -10 + 4n$$

Pour calculer $u_{100}$, on substitue $n$ par $100$ dans l'expression de $u_n$ :

$$u_{100} = -10 + 4 \times 100 = -10 + 400 = 390$$

Donc, $u_n = -10 + 4n$ et $u_{100} = 390$.

b. Cas où $u_1 = 7$ et $r = -2$ :

Ici, le terme connu est $u_1$, donc on utilise $p=1$. La formule devient :

$$u_n = u_1 + (n-1)r$$

En remplaçant $u_1$ et $r$ par leurs valeurs, on obtient :

$$u_n = 7 + (n-1)(-2) = 7 - 2(n-1) = 7 - 2n + 2 = 9 - 2n$$

Pour calculer $u_{100}$, on substitue $n$ par $100$ dans l'expression de $u_n$ :

$$u_{100} = 9 - 2 \times 100 = 9 - 200 = -191$$

Donc, $u_n = 9 - 2n$ et $u_{100} = -191$.

Conclusion : L'expression du terme général d'une suite arithmétique est toujours de la forme $u_n = an + b$, où $a$ est la raison de la suite et $b$ est une constante qui dépend du premier terme.

Correction :

Pour déterminer la raison $r$ d'une suite arithmétique connaissant deux termes, nous utilisons la relation :

$$u_n = u_p + (n-p)r$$

Ici, nous connaissons $u_3 = 11$ et $u_7 = 27$. Nous pouvons donc écrire :

$$u_7 = u_3 + (7-3)r$$

$$27 = 11 + 4r$$

Maintenant, nous résolvons cette équation pour trouver $r$ :

$$4r = 27 - 11$$

$$4r = 16$$

$$r = \dfrac{16}{4} = 4$$

La raison de la suite arithmétique est donc $r = 4$.

Maintenant que nous connaissons la raison $r=4$ et un terme, par exemple $u_3 = 11$, nous pouvons trouver $u_0$ en utilisant la formule du terme général :

$$u_3 = u_0 + (3-0)r$$

$$11 = u_0 + 3 \times 4$$

$$11 = u_0 + 12$$

$$u_0 = 11 - 12 = -1$$

Le premier terme de la suite est donc $u_0 = -1$.

Conclusion : Pour trouver la raison d'une suite arithmétique à partir de deux termes, on utilise la différence entre les termes et on la divise par la différence des indices. Ensuite, on utilise la formule du terme général pour retrouver le premier terme.

Correction :

Pour montrer qu'une suite $(u_n)$ n'est pas arithmétique, il faut vérifier que la différence entre deux termes consécutifs $u_{n+1} - u_n$ n'est pas constante, c'est-à-dire qu'elle dépend de $n$.

Calculons $u_{n+1}$ en remplaçant $n$ par $n+1$ dans l'expression de $u_n$ :

$$u_{n+1} = (n+1)^2 + 1$$

$$u_{n+1} = (n^2 + 2n + 1) + 1$$

$$u_{n+1} = n^2 + 2n + 2$$

Maintenant, calculons la différence $u_{n+1} - u_n$ :

$$u_{n+1} - u_n = (n^2 + 2n + 2) - (n^2 + 1)$$

$$u_{n+1} - u_n = n^2 + 2n + 2 - n^2 - 1$$

$$u_{n+1} - u_n = 2n + 1$$

La différence $u_{n+1} - u_n = 2n + 1$ dépend de $n$. Elle n'est pas constante. Par exemple :

Pour $n = 0$, $u_1 - u_0 = 2 \times 0 + 1 = 1$

Pour $n = 1$, $u_2 - u_1 = 2 \times 1 + 1 = 3$

Pour $n = 2$, $u_3 - u_2 = 2 \times 2 + 1 = 5$

Les différences entre les termes consécutifs ne sont pas les mêmes. Donc, la suite $(u_n)$ n'est pas arithmétique.

Conclusion : Une suite est arithmétique si et seulement si la différence entre deux termes consécutifs est constante. Ici, cette différence dépend de $n$, donc la suite n'est pas arithmétique.

Correction :

Nous savons que $(u_n)$ est une suite arithmétique de raison $r = -3$ et que $u_{50} = 7$. Nous voulons déterminer $u_0$.

On utilise la formule du terme général d'une suite arithmétique :

$$u_n = u_0 + (n-0)r = u_0 + nr$$

Nous connaissons $u_{50}$, donc nous pouvons utiliser cette formule avec $n = 50$ :

$$u_{50} = u_0 + 50r$$

Nous remplaçons $u_{50}$ par $7$ et $r$ par $-3$ :

$$7 = u_0 + 50 \times (-3)$$

$$7 = u_0 - 150$$

Pour trouver $u_0$, nous ajoutons $150$ aux deux côtés de l'équation :

$$u_0 = 7 + 150$$

$$u_0 = 157$$

Donc, le premier terme de la suite est $u_0 = 157$.

Vérification : Calculons $u_{50}$ à partir de $u_0 = 157$ et $r = -3$ :

$$u_{50} = u_0 + 50r = 157 + 50 \times (-3) = 157 - 150 = 7$$

Cela correspond bien à l'énoncé.

Conclusion : Pour retrouver le premier terme d'une suite arithmétique lorsqu'on connaît un autre terme et la raison, on utilise la formule du terme général en "remontant" dans la suite.

Correction :

Le sens de variation d'une suite arithmétique est déterminé par le signe de sa raison $r$.

Si $r > 0$, la suite est strictement croissante.

Si $r < 0$, la suite est strictement décroissante.

Si $r = 0$, la suite est constante.

a. $u_0 = 3$ et $r = 2$ :

La raison $r = 2$ est positive ($r > 0$). Donc, la suite $(u_n)$ est strictement croissante.

b. $u_0 = -3$ et $r = -2$ :

La raison $r = -2$ est négative ($r < 0$). Donc, la suite $(u_n)$ est strictement décroissante.

c. $u_0 = 3$ et $r = -2$ :

La raison $r = -2$ est négative ($r < 0$). Donc, la suite $(u_n)$ est strictement décroissante.

d. $u_0 = -3$ et $r = 2$ :

La raison $r = 2$ est positive ($r > 0$). Donc, la suite $(u_n)$ est strictement croissante.

Remarque : Le premier terme $u_0$ n'influence pas le sens de variation de la suite, seule la raison $r$ compte.

Conclusion : Pour déterminer le sens de variation d'une suite arithmétique, il suffit de regarder le signe de sa raison.

Correction :

Pour déterminer le sens de variation d'une suite définie par son terme général $u_n$ en fonction de $n$, nous devons identifier si c'est une suite arithmétique et, si oui, trouver sa raison.

Rappel : L'expression du terme général d'une suite arithmétique est de la forme $u_n = u_0 + nr = rn + u_0$, où $r$ est la raison et $u_0$ est le premier terme.

a. $u_n = -3 + 5n$ :

On peut réécrire cette expression sous la forme $u_n = 5n - 3$. C'est de la forme $u_n = rn + u_0$ avec $r = 5$ et $u_0 = -3$. Donc, $(u_n)$ est une suite arithmétique de raison $r = 5$. Puisque $r = 5 > 0$, la suite $(u_n)$ est strictement croissante.

b. $u_n = 3 - 5n$ :

On peut réécrire cette expression sous la forme $u_n = -5n + 3$. C'est de la forme $u_n = rn + u_0$ avec $r = -5$ et $u_0 = 3$. Donc, $(u_n)$ est une suite arithmétique de raison $r = -5$. Puisque $r = -5 < 0$, la suite $(u_n)$ est strictement décroissante.

c. $u_n = \dfrac{5 - 4n}{7}$ :

On peut réécrire cette expression en séparant la fraction :

$$u_n = \dfrac{5}{7} - \dfrac{4n}{7} = -\dfrac{4}{7}n + \dfrac{5}{7}$$

C'est de la forme $u_n = rn + u_0$ avec $r = -\dfrac{4}{7}$ et $u_0 = \dfrac{5}{7}$. Donc, $(u_n)$ est une suite arithmétique de raison $r = -\dfrac{4}{7}$. Puisque $r = -\dfrac{4}{7} < 0$, la suite $(u_n)$ est strictement décroissante.

Conclusion : Pour déterminer le sens de variation d'une suite donnée par son terme général $u_n$, on identifie la raison $r$ si c'est une suite arithmétique. Le signe de $r$ donne le sens de variation.

Correction :

Pour représenter graphiquement les premiers termes d'une suite arithmétique, nous devons calculer ces termes et placer les points correspondants dans un repère.

Nous avons $u_0 = -5$ et la raison $r = 2$. Calculons les premiers termes :

$u_0 = -5$

$u_1 = u_0 + r = -5 + 2 = -3$

$u_2 = u_1 + r = -3 + 2 = -1$

$u_3 = u_2 + r = -1 + 2 = 1$

$u_4 = u_3 + r = 1 + 2 = 3$

Les cinq premiers termes sont donc : $u_0 = -5$, $u_1 = -3$, $u_2 = -1$, $u_3 = 1$, $u_4 = 3$.

Représentation graphique (à réaliser par l'élève) : Sur le repère, marquer les points suivants : (0, -5), (1, -3), (2, -1), (3, 1), et (4, 3). Ces points doivent être alignés, formant une droite qui monte car la raison est positive.

Conclusion : La représentation graphique d'une suite arithmétique est un ensemble de points alignés. Placer ces points permet de visualiser la progression de la suite.

Correction :

1. Déterminer $u_0$ et la raison $r$ :

Sur le graphique fourni (image: arithmetique/suite_repere_22.png), nous pouvons lire les coordonnées des premiers points. Le premier terme $u_0$ correspond à l'ordonnée du point d'abscisse $0$. En regardant le graphique, on constate que le point pour $n=0$ a pour coordonnées $(0; 1,5)$. Donc, le premier terme est $u_0 = 1,5$.

Pour déterminer la raison $r$, nous observons la variation entre deux points consécutifs. Prenons par exemple les points pour $n=0$ et $n=1$. Pour $n=0$, $u_0 = 1,5$. Pour $n=1$, en lisant le graphique, on trouve le point $(1; 1)$, donc $u_1 = 1$. La raison $r$ est la différence entre deux termes consécutifs :

$$r = u_1 - u_0 = 1 - 1,5 = -0,5$$

Vérifions avec les points suivants. Pour $n=1$, $u_1 = 1$. Pour $n=2$, on lit environ $(2; 0,5)$, donc $u_2 = 0,5$. La différence est $u_2 - u_1 = 0,5 - 1 = -0,5$. La raison semble constante et égale à $r = -0,5$. Comme la raison est négative, la suite est décroissante, ce qui est cohérent avec un graphique descendant.

Ainsi, nous avons $u_0 = 1,5$ et $r = -0,5$.

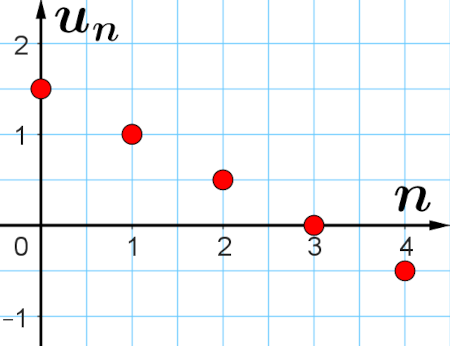
2. Donner l'expression de $u_n$ en fonction de $n$ :

Nous utilisons la formule du terme général d'une suite arithmétique :

$$u_n = u_0 + nr$$

En remplaçant $u_0$ et $r$ par les valeurs trouvées ($u_0 = 1,5$ et $r = -0,5$), on obtient :

$$u_n = 1,5 + n \times (-0,5)$$

$$u_n = 1,5 - 0,5n$$

Donc, l'expression de $u_n$ en fonction de $n$ est $u_n = 1,5 - 0,5n$.

Conclusion : L'analyse graphique d'une suite arithmétique permet de déterminer visuellement le premier terme et la raison en observant la position des points et leur variation. On peut ensuite confirmer ces valeurs et trouver l'expression du terme général.

Correction :

1. Déterminer $u_0$, $u_1$ et $u_2$ :

En examinant le graphique fourni (image: arithmetique/suite_repere_3.png), nous lisons les ordonnées des points correspondant à $n=0$, $n=1$ et $n=2$.

Pour $n=0$, le point semble être à l'ordonnée $2$, donc $u_0 = 2$.

Pour $n=1$, le point est à l'ordonnée $1,5$, donc $u_1 = 1,5$.

Pour $n=2$, le point est à l'ordonnée $0,5$, donc $u_2 = 0,5$.

Ainsi, nous avons approximativement $u_0 = 2$, $u_1 = 1,5$ et $u_2 = 0,5$. (Note : une lecture graphique peut être légèrement imprécise, mais nous prendrons ces valeurs pour notre analyse).

2. Cette suite peut-elle être arithmétique ?

Pour qu'une suite soit arithmétique, la différence entre deux termes consécutifs doit être constante. Calculons les différences entre les premiers termes que nous avons identifiés graphiquement :

Différence entre $u_1$ et $u_0$ : $u_1 - u_0 = 1,5 - 2 = -0,5$

Différence entre $u_2$ et $u_1$ : $u_2 - u_1 = 0,5 - 1,5 = -1$

Nous constatons que les différences ne sont pas les mêmes : $-0,5 \neq -1$. La différence entre les termes consécutifs n'est pas constante. Visuellement sur le graphique, on peut observer que "la descente" entre $u_0$ et $u_1$ n'est pas de la même amplitude que "la descente" entre $u_1$ et $u_2$. Si la suite était arithmétique, les points seraient alignés sur une droite, ce qui ne semble pas être le cas ici.

Par conséquent, la suite $(u_n)$ n'est pas arithmétique.

Conclusion : L'examen graphique et le calcul des différences entre termes consécutifs montrent que cette suite n'est pas arithmétique. La non-constance des différences, visible à l'œil nu sur le graphique par un espacement irrégulier verticalement entre les points consécutifs, confirme cette conclusion.

Correction :

Pour déterminer si une suite définie par son terme général est arithmétique, on vérifie si elle est de la forme $u_n = rn + u_0$, ou si la différence $u_{n+1} - u_n$ est constante.

a. $a_n = 3n - 2$ :

C'est de la forme $a_n = rn + a_0$ avec $r = 3$ et $a_0 = -2$. Donc, $(a_n)$ est une suite arithmétique de raison $r = 3$ et de premier terme $a_0 = -2$.

b. $b_n = \dfrac{2n+3}{4}$ :

On peut réécrire $b_n = \dfrac{2}{4}n + \dfrac{3}{4} = \dfrac{1}{2}n + \dfrac{3}{4}$. C'est de la forme $b_n = rn + b_0$ avec $r = \dfrac{1}{2}$ et $b_0 = \dfrac{3}{4}$. Donc, $(b_n)$ est une suite arithmétique de raison $r = \dfrac{1}{2}$ et de premier terme $b_0 = \dfrac{3}{4}$.

c. $c_n = (n+1)^2 - n^2$ :

Développons et simplifions l'expression :

$$c_n = (n^2 + 2n + 1) - n^2 = n^2 + 2n + 1 - n^2 = 2n + 1$$

C'est de la forme $c_n = rn + c_0$ avec $r = 2$ et $c_0 = 1$. Donc, $(c_n)$ est une suite arithmétique de raison $r = 2$ et de premier terme $c_0 = 1$.

d. $d_n = n^2 + n$ :

Calculons $d_{n+1} - d_n$ :

$$d_{n+1} = (n+1)^2 + (n+1) = n^2 + 2n + 1 + n + 1 = n^2 + 3n + 2$$

$$d_{n+1} - d_n = (n^2 + 3n + 2) - (n^2 + n) = n^2 + 3n + 2 - n^2 - n = 2n + 2$$

La différence $d_{n+1} - d_n = 2n + 2$ dépend de $n$. Elle n'est pas constante. Donc, $(d_n)$ n'est pas une suite arithmétique.

Conclusion : Les suites (a), (b), et (c) sont arithmétiques, tandis que la suite (d) ne l'est pas. Reconnaître la forme $rn+u_0$ ou vérifier que la différence entre termes consécutifs est constante sont les méthodes clés.

Correction :

Pour déterminer si une suite est arithmétique lorsqu'elle est définie par récurrence ou par une description, nous devons vérifier si la différence entre termes consécutifs est constante.

a. $\left\{ \begin{array}{l} u_0 = 4 \\ u_{n+1} = -0.9 + u_n \end{array} \right.$ :

La relation de récurrence est de la forme $u_{n+1} = u_n + r$ avec $r = -0.9$. C'est la définition même d'une suite arithmétique. Donc, $(u_n)$ est une suite arithmétique de raison $r = -0.9$ et de premier terme $u_0 = 4$.

b. $\left\{ \begin{array}{l} v_0 = 4 \\ v_{n+1} = 3 + \dfrac{1}{2}v_n \end{array} \right.$ :

Cette relation de récurrence n'est pas de la forme $v_{n+1} = v_n + r$. Ici, $v_{n+1}$ est obtenu en multipliant $v_n$ par $\dfrac{1}{2}$ et en ajoutant $3$. Calculons les premiers termes pour vérifier :

$v_0 = 4$

$v_1 = 3 + \dfrac{1}{2}v_0 = 3 + \dfrac{1}{2}(4) = 3 + 2 = 5$

$v_2 = 3 + \dfrac{1}{2}v_1 = 3 + \dfrac{1}{2}(5) = 3 + 2.5 = 5.5$

Les différences : $v_1 - v_0 = 5 - 4 = 1$ et $v_2 - v_1 = 5.5 - 5 = 0.5$. Les différences ne sont pas constantes. Donc, $(v_n)$ n'est pas une suite arithmétique.

c. $w_n = \dfrac{3}{n+2}$ :

Calculons les premiers termes :

$w_0 = \dfrac{3}{0+2} = \dfrac{3}{2} = 1.5$

$w_1 = \dfrac{3}{1+2} = \dfrac{3}{3} = 1$

$w_2 = \dfrac{3}{2+2} = \dfrac{3}{4} = 0.75$

Les différences : $w_1 - w_0 = 1 - 1.5 = -0.5$ et $w_2 - w_1 = 0.75 - 1 = -0.25$. Les différences ne sont pas constantes. Donc, $(w_n)$ n'est pas une suite arithmétique.

d. $t_n = \dfrac{n^2-1}{n+1}$ :

Pour $n \neq -1$, on peut simplifier l'expression : $t_n = \dfrac{(n-1)(n+1)}{n+1} = n-1$. Donc, $t_n = n - 1$. C'est de la forme $t_n = rn + t_0$ avec $r = 1$ et $t_0 = -1$. Donc, $(t_n)$ est une suite arithmétique de raison $r = 1$ et de premier terme $t_0 = -1$ (pour $n \ge 0$).

e. La suite des multiples de $4$ :

Les multiples de $4$ sont : $0, 4, 8, 12, 16, \dots$. On peut écrire cette suite comme $(m_n)$ avec $m_n = 4n$ pour $n \in \mathbb{N}$. C'est de la forme $m_n = rn + m_0$ avec $r = 4$ et $m_0 = 0$. Donc, $(m_n)$ est une suite arithmétique de raison $r = 4$ et de premier terme $m_0 = 0$.

Conclusion : Reconnaître la forme de la définition par récurrence ou du terme général, ou calculer les premiers termes et vérifier la constance de la différence sont les méthodes à utiliser pour identifier les suites arithmétiques dans différents types de définitions.

Correction :

1. Suite $(u_n)$ : $u_0 = -2$, $r = 5$, déterminer $u_{15}$ :

Utilisons la formule du terme général : $u_n = u_0 + nr$. Pour $n = 15$ :

$$u_{15} = u_0 + 15r = -2 + 15 \times 5 = -2 + 75 = 73$$

Donc, $u_{15} = 73$.

2. Suite $(v_n)$ : $v_6 = 4$, $r = -3$, déterminer $v_{15}$ :

Utilisons la formule $u_n = u_p + (n-p)r$ avec $p = 6$ et $n = 15$ :

$$v_{15} = v_6 + (15-6)r = v_6 + 9r = 4 + 9 \times (-3) = 4 - 27 = -23$$

Donc, $v_{15} = -23$.

3. Suite $(w_n)$ : $w_4 = 2$, $w_{10} = 14$, déterminer $r$ et $w_0$ :

Utilisons $w_{10} = w_4 + (10-4)r$ :

$$14 = 2 + 6r$$

$$6r = 14 - 2 = 12$$

$$r = \dfrac{12}{6} = 2$$

La raison est $r = 2$. Maintenant, trouvons $w_0$ en utilisant $w_4 = w_0 + 4r$ :

$$2 = w_0 + 4 \times 2$$

$$2 = w_0 + 8$$

$$w_0 = 2 - 8 = -6$$

Donc, $r = 2$ et $w_0 = -6$.

4. Suite $(t_n)$ : $t_2 + t_3 + t_4 = 12$, déterminer $t_3$ :

Dans une suite arithmétique, $t_3$ est la moyenne arithmétique de $t_2$ et $t_4$. On peut aussi exprimer $t_2$ et $t_4$ en fonction de $t_3$ et de la raison $r$ :

$t_2 = t_3 - r$

$t_4 = t_3 + r$

Donc, $t_2 + t_3 + t_4 = (t_3 - r) + t_3 + (t_3 + r) = 3t_3$. Nous avons :

$$3t_3 = 12$$

$$t_3 = \dfrac{12}{3} = 4$$

Donc, $t_3 = 4$.

Conclusion : Ces exercices montrent comment utiliser la formule du terme général et les propriétés des suites arithmétiques pour calculer des termes spécifiques ou déterminer la raison et le premier terme à partir d'informations données.

Correction :

1. Conjecture sur la nature de la suite $(u_n)$ :

Observons les valeurs données dans le tableur. Calculons les différences entre les termes consécutifs :

$u_1 - u_0 = 1 - 5 = -4$

$u_2 - u_1 = -3 - 1 = -4$

$u_3 - u_2 = -7 - (-3) = -7 + 3 = -4$

$u_4 - u_3 = -11 - (-7) = -11 + 7 = -4$

La différence entre les termes consécutifs semble constante et égale à $-4$. On peut conjecturer que la suite $(u_n)$ est une suite arithmétique de raison $r = -4$ et de premier terme $u_0 = 5$ (valeur en A1).

2. Valeur de la cellule A1 et A100 :

La cellule A1 correspond au premier terme, $u_0$. D'après le tableur, la valeur en A1 est $5$. Donc, $u_0 = 5$.

Pour trouver la valeur en A100, qui correspond à $u_{99}$ (car A1 correspond à $u_0$, A2 à $u_1$, etc.), nous utilisons la formule du terme général : $u_n = u_0 + nr$. Ici, $n = 99$, $u_0 = 5$, et $r = -4$ :

$$u_{99} = u_0 + 99r = 5 + 99 \times (-4) = 5 - 396 = -391$$

Donc, la valeur de la cellule A100 est $u_{99} = -391$.

Conclusion : L'observation des différences dans un tableur peut suggérer qu'une suite est arithmétique. On utilise ensuite les propriétés des suites arithmétiques pour calculer des termes plus éloignés.

Correction :

1. Nombre d'entiers dans l'intervalle I=[17; 154] :

Pour trouver le nombre d'entiers dans l'intervalle $[a; b]$ où $a$ et $b$ sont des entiers, on utilise la formule : Nombre d'entiers = $b - a + 1$.

Ici, $a = 17$ et $b = 154$. Donc, le nombre d'entiers dans I est :

$$154 - 17 + 1 = 137 + 1 = 138$$

Il y a 138 nombres entiers dans l'intervalle [17; 154].

2. Nombre de nombres pairs dans l'intervalle I=[17; 154] :

Le premier nombre pair dans l'intervalle [17; 154] est 18 et le dernier est 154. Les nombres pairs forment une suite arithmétique de raison 2 et de premier terme 18. Nous cherchons le nombre de termes de cette suite allant de 18 à 154.

Soit la suite des nombres pairs $(p_n)$ telle que $p_1 = 18$, $p_2 = 20$, ..., $p_N = 154$. On a $p_n = 18 + (n-1)2$. On veut trouver $N$ tel que $p_N = 154$ :

$$154 = 18 + (N-1)2$$

$$154 - 18 = (N-1)2$$

$$136 = (N-1)2$$

$$\dfrac{136}{2} = N-1$$

$$68 = N-1$$

$$N = 68 + 1 = 69$$

Il y a 69 nombres pairs dans l'intervalle [17; 154].

3. Nombre de multiples de 4 dans l'intervalle I=[17; 154] :

Le premier multiple de 4 dans l'intervalle [17; 154] est 20 et le dernier est 152. Les multiples de 4 forment une suite arithmétique de raison 4 et de premier terme 20. Nous cherchons le nombre de termes de cette suite allant de 20 à 152.

Soit la suite des multiples de 4 $(q_n)$ telle que $q_1 = 20$, $q_2 = 24$, ..., $q_M = 152$. On a $q_n = 20 + (n-1)4$. On veut trouver $M$ tel que $q_M = 152$ :

$$152 = 20 + (M-1)4$$

$$152 - 20 = (M-1)4$$

$$132 = (M-1)4$$

$$\dfrac{132}{4} = M-1$$

$$33 = M-1$$

$$M = 33 + 1 = 34$$

Il y a 34 multiples de 4 dans l'intervalle [17; 154].

Conclusion : Les suites arithmétiques sont utiles pour dénombrer des éléments dans des intervalles, notamment les nombres pairs, les multiples d'un nombre, etc.

def suite_u(n):
    u = 4
    for i in range(1, n + 1):
        u = u - 2
    print(u)

# Pour n=3, executer :
suite_u(3)
                                    

Correction :

1. Valeur affichée si $n=3$ :

Suivons l'algorithme pas à pas avec $n=3$ :

Initialisation : $u \leftarrow 4$

Boucle POUR $i$ allant de $1$ à $3$ :

Pour $i=1$ : $u \leftarrow u - 2 = 4 - 2 = 2$

Pour $i=2$ : $u \leftarrow u - 2 = 2 - 2 = 0$

Pour $i=3$ : $u \leftarrow u - 2 = 0 - 2 = -2$

Afficher $u$. La valeur affichée sera $-2$.

2. La suite $u$ est-elle arithmétique ? Raison et premier terme :

L'algorithme commence avec $u = 4$. À chaque itération de la boucle, on soustrait $2$ à $u$. Cela signifie que chaque terme de la suite est obtenu en ajoutant $-2$ au terme précédent. C'est la définition d'une suite arithmétique de raison $r = -2$.

Le premier terme de la suite est la valeur initiale de $u$, qui est $4$. Donc, le premier terme est $u_0 = 4$ (ou $u_1$ si on commence l'indexation à 1, selon comment on interprète "premier terme" dans ce contexte). Si on considère que l'algorithme calcule $u_n$ après $n$ itérations de la boucle, et que l'initialisation donne $u$ avant la première itération, alors on peut considérer le premier terme comme étant avant la boucle, donc $u_0 = 4$.

Si on note $u_i$ la valeur de $u$ après $i$ itérations de la boucle, alors :

$u_0 = 4$ (valeur initiale)

$u_1 = u_0 - 2 = 4 - 2 = 2$

$u_2 = u_1 - 2 = 2 - 2 = 0$

$u_3 = u_2 - 2 = 0 - 2 = -2$

La suite $(u_n)$ est arithmétique de raison $r = -2$ et de premier terme $u_0 = 4$.

Conclusion : Les algorithmes peuvent définir des suites, et dans ce cas, l'algorithme décrit une suite arithmétique. L'analyse de l'algorithme permet de déterminer la nature de la suite, sa raison et son premier terme.