Polynôme du second degré
Ici, vous trouverez une série d'exercices pour vous entraîner sur les polynômes du second degré, un outil fondamental en mathématiques. Ces exercices couvrent la reconnaissance des polynômes du second degré, la détermination des coefficients, la forme canonique, le tableau de variations, la parabole, le sommet et des problèmes d'optimisation.
Revoyons ensemble les points essentiels sur les polynômes du second degré avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Définition d'un polynôme du second degré
Un polynôme du second degré, aussi appelé trinôme, est une fonction $f$ qui peut s'écrire sous la forme:
$$f(x) = ax^2 + bx + c$$
où $a$, $b$, et $c$ sont des nombres réels, avec $a \neq 0$. Les coefficients sont :
- $a$ : coefficient de $x^2$
- $b$ : coefficient de $x$
- $c$ : terme constant
La représentation graphique d'un polynôme du second degré est une parabole.
2. Forme canonique
Tout polynôme du second degré peut être écrit sous sa forme canonique :
$$f(x) = a(x-\alpha)^2 + \beta$$
où $a$ est le même coefficient qu'avant, et $(\alpha ; \beta)$ sont les coordonnées du sommet de la parabole. On a les formules pour trouver $\alpha$ et $\beta$ :
$$\alpha = -\dfrac{b}{2a}$$
$$\beta = f(\alpha)$$
La forme canonique est très utile pour déterminer le tableau de variations et le sommet de la parabole.
3. Tableau de variations
Le tableau de variations d'un polynôme du second degré dépend du signe de $a$.
Cas 1 : $a > 0$ (parabole tournée vers le haut)
La fonction est d'abord décroissante, puis croissante. Elle admet un minimum en $x = \alpha$, qui vaut $\beta$.
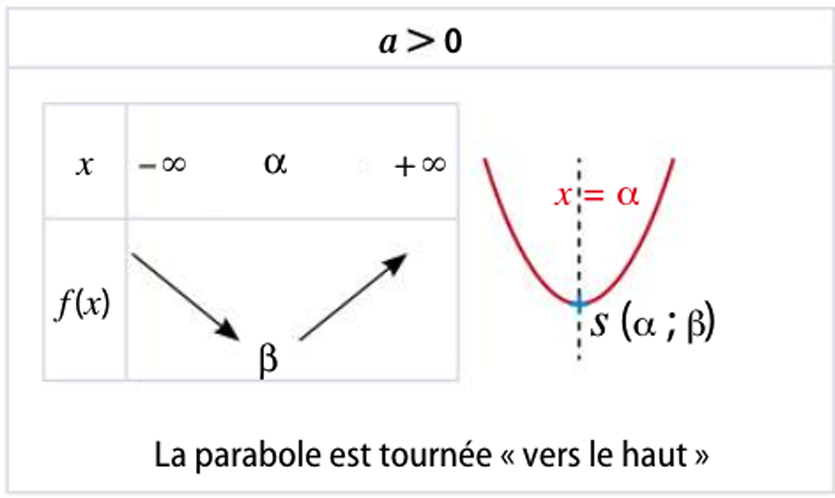
Cas 2 : $a < 0$ (parabole tournée vers le bas)
La fonction est d'abord croissante, puis décroissante. Elle admet un maximum en $x = \alpha$, qui vaut $\beta$.
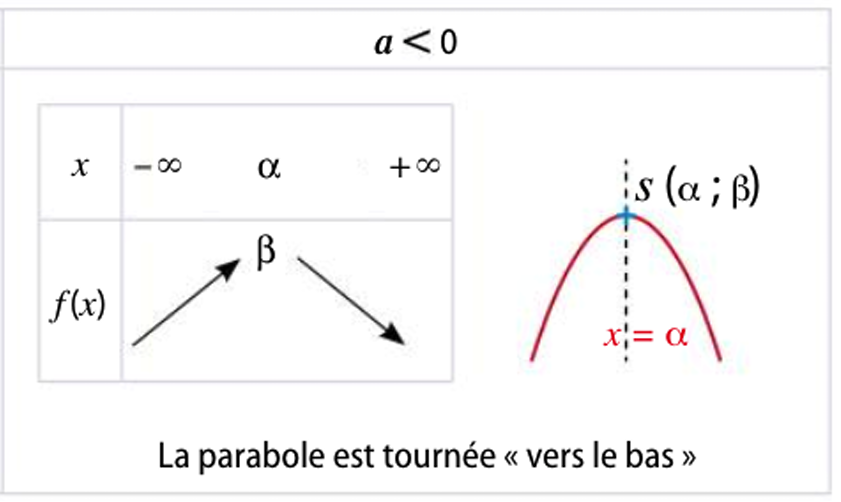
4. Sommet de la parabole
Le sommet $S$ de la parabole représentative d'un polynôme du second degré $f(x) = ax^2 + bx + c$ a pour coordonnées $(\alpha ; \beta)$, où :
$$\alpha = -\dfrac{b}{2a} \quad \text{et} \quad \beta = f(\alpha)$$
En forme canonique $f(x) = a(x-\alpha)^2 + \beta$, les coordonnées du sommet sont directement lisibles : $S(\alpha ; \beta)$.
L'axe de symétrie de la parabole est la droite verticale d'équation $x = \alpha$.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
Dans chaque cas, dire s'il s'agit d'une fonction polynôme du second degré. Dans l'affirmative, donner les coefficients $a$, $b$, $c$.
a. $-2x^2+5$
b. $(1-2x)^2$
c. $\dfrac{x^2+6x-1}3$
d. $(3x-2)^2-9x^2$
Exercice 2
Dans chaque cas, on a tracé la parabole représentant une fonction polynôme $f$ du second degré. À l'aide du graphique, déterminer l'expression de $f(x)$:
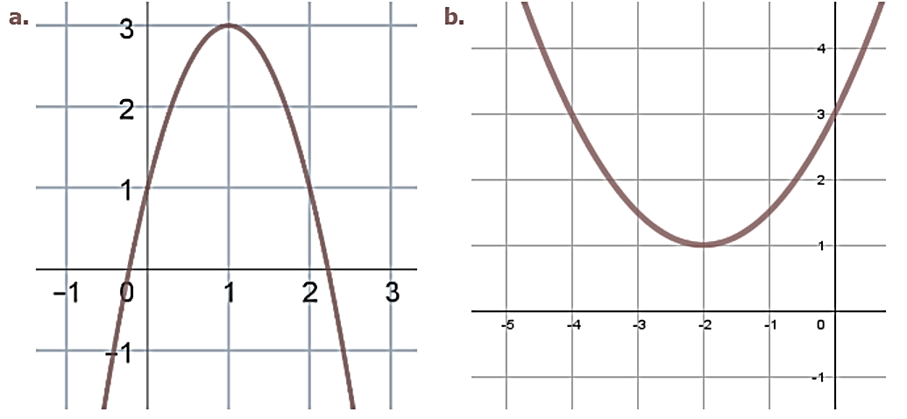
Exercice 3
On a représenté les courbes de cinq fonctions: $f, g, h, k, m$.
$f(x)=x^2-6x+8$
$g(x)=-2x^2+2x+1$
$h(x)=2x-1$
$k(x)=(x-1)^2+3$
$m(x)=x^2+4x+4$
Associer à chaque courbe, la fonction qui lui correspond, en justifiant:
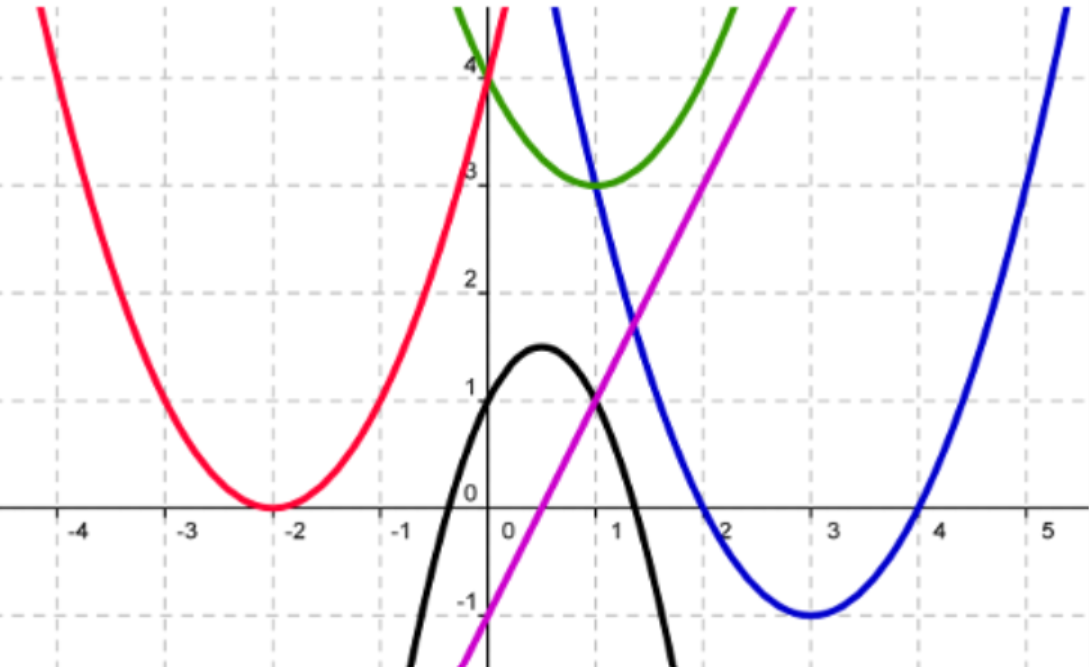
Exercice 4
Déterminer le tableau de variations des fonctions polynômes du second degré suivantes:
a. $f: x\mapsto 4(x-3)^2+5$
b. $x\mapsto 2-(x+1)^2$
c. $h: x\mapsto 1-4x^2$
Exercice 5
On donne le tableau de variation d'une fonction $f$:
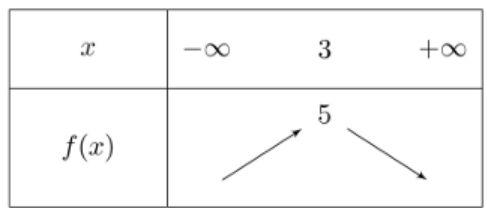
Parmi les fonctions suivantes, une est $f$. Laquelle? Justifier.
$ x\mapsto (x-3)^2+5$
$ x\mapsto (x+3)^2+5$
$ x\mapsto -(x-3)^2+5$
$ x\mapsto -(x-5)^2+3$
Exercice 6
Écrire la fonction polynôme du second degré $f$ définie par $f(x)=3x^2+12x+8$ sous forme canonique :
1. En utilisant la formule du cours sur $\alpha$
2. En utilisant votre calculatrice pour avoir les coordonnées du sommet
3. En utilisant la méthode de complétion du carré
Exercice 7
Écrire la fonction polynôme du second degré $f$ sous forme canonique par $2$ méthodes : $f(x)=2x^2+16x+27$.
Exercice 8
Déterminer le tableau de variations du trinôme: $f(x)=-5x^2+10x+2$.
Exercice 9
1. Déterminer la forme canonique du trinôme: $f(x)=-2x^2+12x-17$.
2. En déduire le tableau de variations de $f$.
Exercice 10
Dans chaque cas, déterminer la forme canonique des trinômes suivants:
a. $x^2+6x+1$
b. $-2x^2+5$
c. $2x^2+x$
d. $(1-2x)^2$
Exercice 11
On note $\mathscr{P}$ la parabole représentant la fonction $f$. Dans chaque cas, déterminer les coordonnées du sommet de $\mathscr{P}$:
a. $f(x)=-x^2+4x+1$
b. $f(x)=2(x+3)^2-7$
c. $f(x)=(1-x)(x+3)$
Exercice 12
Soit $f$ un polynôme du $2^{\text{nd}}$ degré tel que $f(2)=3$ et $f(10)=3$. Déterminer l'abscisse du sommet.
Exercice 13
Variations, maximum et minimum d'un polynôme du second degré - Première spé maths S ES STI
a. $f(x)=x^2-2x+3$
b. $f(x)=-2(x+1)^2-3$
c. $f(x)=(4-2x)(x-3)$
Exercice 14
Soit une parabole qui admet pour sommet le point (2;1) et qui passe par le point (1;3). Déterminer la fonction $f$ qui correspond à cette parabole.
Exercice 15
Préciser si les affirmations suivantes sont vraies ou fausses:
1. La courbe de la fonction $f(x)=2(1-x)^2-3$ est une parabole tournée vers le haut.
2. La courbe de la fonction $f(x)=-2x^2+12x-17$ est une parabole et son sommet a pour abscisse 3.
3. La courbe de la fonction $f(x)=3(x+2)^2+5$ est une parabole et le sommet a pour coordonnées (-2;5).
Exercice 16
Dans chaque cas, indiquer la ou les bonnes réponses:
1.
Soit $f$ définie sur $\mathbb{R}$ par $f(x)=3(x-1)^2-2$:
a.
$f$ est croissante sur $[1;+\infty[$.
b.
Pour $x\leqslant 1$, $f(x)\leqslant 0$.
c.
$f$ admet un maximum en $1$.
2.
Soit $f$ définie sur $\mathbb{R}$ par $f(x)=-(x+4)^2-3$:
a.
Le maximum de $f$ est $4$.
b.
$f$ admet un maximum en $-4$.
c.
Pour tout $x$, $f(x)\leqslant 0$.
3.
Soit $f:x\rightarrow -3(x-4)^2+7$:
a.
L'équation $f(x)=8$ admet des solutions.
b.
L'équation $f(x)=0$ admet 2 solutions.
Exercice 17
Un pompiste vend le litre d'essence au prix de $1,20$ € . Le prix d'achat est pour lui de $0,85$ €, le litre. Il sait qu'il peut compter sur une vente journalière de $1 000$ litres et qu'à chaque baisse de $1$ centime qu'il consent pour le prix du litre, il vendra $100$ litres de plus par jour. À quel prix le pompiste doit-il vendre le litre d'essence pour faire un bénéfice maximal et quelle est la valeur de ce bénéfice maximal ?
Exercice 18
$ABCD$ est un carré de côté $10$ cm et $M$ est un point de $[AB]$ (distinct de $A$ et de $B$) et $AMON$ est un carré de côté $x$.
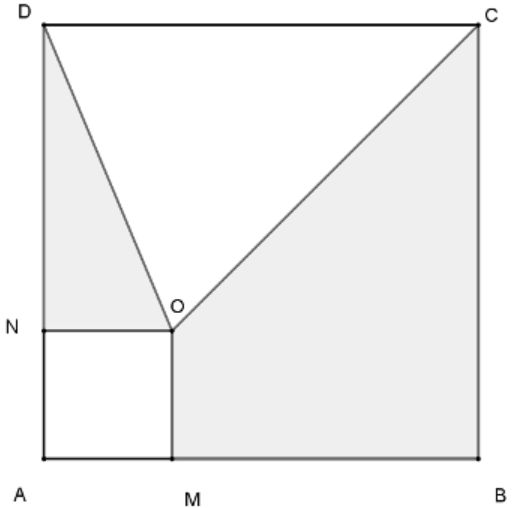
1. Montrer que l'aire grise (en $\text{cm}^2$) s'écrit $-x^2 + 5x + 50$.
2. Où placer le point $M$ pour obtenir la plus grande aire grise possible ? Que vaut alors l'aire grise ?
Exercice 19
Une agence immobilière possède $200$ studios qui sont tous occupés quand le loyer est de $700$ euros par mois. L'agence estime qu'à chaque fois qu'elle augmente le loyer de $5$ euros, un appartement n'est plus loué. On note $x$ le nombre d'augmentations de $5$ euro sur le loyer mensuel.
1. Montrer que le revenu mensuel de l'agence (en euros) s'écrit : $-5x^2 + 300x +140000$.
2. En déduire le montant du loyer pour maximiser le revenu mensuel de l'agence.
3. Dans le contexte de ce problème, quelle est la valeur maximale réaliste pour le nombre d'augmentations de loyer $x$ ? Justifiez votre réponse en considérant le nombre de studios disponibles.
Exercice 20
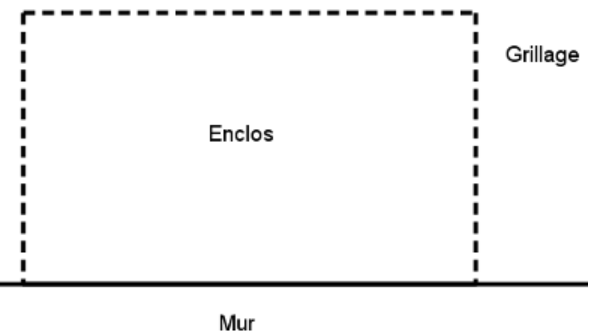
On souhaite délimiter un enclos rectangulaire adossé à un mur à l'aide d'une clôture en grillage de $80$ mètres de long comme indiqué sur le schéma ci-dessous :
Exercice 21
En utilisant la définition d'une fonction strictement croissante sur un intervalle (puis celle d'une
fonction
strictement décroissante), démontrer que :
1. la fonction $f : x \mapsto 2(x-3)^2 -1$ est strictement croissante sur $[3~;~+\infty[$.
2. la fonction $f : x \mapsto -3(x+1)^2 + 5$ est strictement décroissante sur $[-1~;~+\infty[$.
3. la fonction $f : x \mapsto \dfrac{1}{2}(x-2)^2 + 3$ est strictement décroissante sur $]-\infty~;~2]$.







