Position relative de deux courbes
Ici, vous trouverez des exercices pour vous entraîner à déterminer la position relative de deux courbes de fonctions. Maîtriser cette compétence est essentiel pour approfondir votre compréhension des fonctions et de leurs représentations graphiques.
Revoyons ensemble les points essentiels sur la position relative de deux courbes avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Définition de la position relative
Étudier la position relative de deux courbes $\mathscr{C}_f$ et $\mathscr{C}_g$ représentant respectivement les fonctions $f$ et $g$, définies sur un même ensemble, revient à déterminer pour quelles valeurs de $x$ :
• La courbe $\mathscr{C}_f$ est au-dessus de la courbe $\mathscr{C}_g$.
• La courbe $\mathscr{C}_f$ est en-dessous de la courbe $\mathscr{C}_g$.
• Les courbes $\mathscr{C}_f$ et $\mathscr{C}_g$ se coupent.
2. Méthode générale
Pour comparer les positions relatives de $\mathscr{C}_f$ et $\mathscr{C}_g$, on étudie le signe de la différence $d(x) = f(x) - g(x)$.
Calculer et simplifier l'expression $f(x) - g(x)$.
Étudier le signe de $d(x) = f(x) - g(x)$. Pour cela, on cherche à résoudre les inéquations :
• $f(x) - g(x) > 0$ pour déterminer quand $\mathscr{C}_f$ est au-dessus de $\mathscr{C}_g$.
• $f(x) - g(x) < 0$ pour déterminer quand $\mathscr{C}_f$ est en-dessous de $\mathscr{C}_g$.
• $f(x) - g(x) = 0$ pour trouver les points d'intersection des deux courbes.
3. Interprétation graphique du signe de $f(x) - g(x)$
Soit $d(x) = f(x) - g(x)$. Alors :
• Si $f(x) - g(x) > 0$, alors $f(x) > g(x)$, ce qui signifie que la courbe $\mathscr{C}_f$ est au-dessus de la courbe $\mathscr{C}_g$.
• Si $f(x) - g(x) < 0$, alors $f(x) < g(x)$, ce qui signifie que la courbe $\mathscr{C}_f$ est en-dessous de la courbe $\mathscr{C}_g$.
• Si $f(x) - g(x) = 0$, alors $f(x) = g(x)$, ce qui signifie que les courbes $\mathscr{C}_f$ et $\mathscr{C}_g$ se coupent au point d'abscisse $x$. Le point d'intersection a pour coordonnées $(x ; f(x))$ ou $(x ; g(x))$ (puisque $f(x)=g(x)$ à ce point).
4. Résolution d'inéquations
L'étude du signe de $f(x) - g(x)$ nous ramène souvent à la résolution d'inéquations, notamment des inéquations du second degré si $f$ et $g$ sont des fonctions polynomiales de degré au plus 2.
Pour résoudre une inéquation du second degré de la forme $ax^2 + bx + c > 0$ (ou $< 0$, $\geq 0$, $\leq 0$) :
1. Calculer le discriminant $\Delta = b^2 - 4ac$.
2. Déterminer les racines $x_1$ et $x_2$ (s'il y en a) :
• Si $\Delta > 0$, il y a deux racines distinctes : $$x_1 = \dfrac{-b - \sqrt{\Delta}}{2a} \quad \text{et} \quad x_2 = \dfrac{-b + \sqrt{\Delta}}{2a}$$
• Si $\Delta = 0$, il y a une racine double : $$x_0 = \dfrac{-b}{2a}$$
• Si $\Delta < 0$, il n'y a pas de racine réelle.
3. Utiliser le signe du coefficient $a$ et les racines pour déterminer le signe du trinôme $ax^2 + bx + c$ selon les intervalles de valeurs de $x$. On peut s'aider d'un tableau de signes.
Règle de signe : Pour un trinôme $ax^2 + bx + c$ ($a \neq 0$) :
• Si $a > 0$, le trinôme est positif à l'extérieur des racines (si elles existent) et négatif entre les racines.
• Si $a < 0$, le trinôme est négatif à l'extérieur des racines (si elles existent) et positif entre les racines.
• Si $\Delta < 0$, le trinôme est toujours du signe de $a$.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
Soit les fonctions $f$ et $g$ définies sur $\mathbb{R}$ par $f(x)=x^2-6x+1$ et $g(x)=1-x^2$.
Étudier la position relative des courbes de $f$ et $g$ notées respectivement $\mathscr{C}_f$ et $\mathscr{C}_g$.
Exercice 2
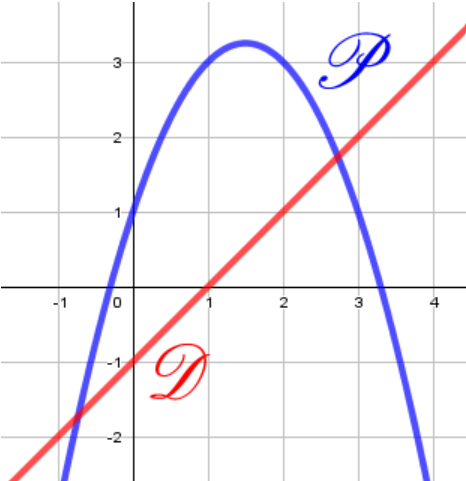
On a tracé la parabole $\mathscr{P}$ représentant la fonction $f$ définie sur $\mathbb{R}$ par $f(x) =-x^2+3x+1$ et la droite $\mathscr{D}$ d'équation $y= x-1$.
Exercice 3
Dans chaque cas, étudier les positions relatives des courbes $\mathscr{C}_f$ et $\mathscr{C}_g$ définie sur $\mathbb{R}$.
- $f(x)=2x^2-3x-2$ et $g(x)=x^2-2x+4$
- $f(x)=-\dfrac 12x^2+3x-1$ et $g(x)=x+1$
Exercice 4
Soit les fonctions $f$ et $g$ définies sur $\mathbb{R}$ par $f(x) = x^2 + 4x + 5$ et $g(x) = -x + 1$. Étudier la position relative de $\mathscr{C}_f$ et $\mathscr{C}_g$.
Exercice 5
Soit les fonctions $f(x) = -2x^2 + 8x - 5$ et $g(x) = x^2 - 4x + 3$. Étudier la position relative de $\mathscr{C}_f$ et $\mathscr{C}_g$.
Exercice 6
Soit $f(x) = x^2 - 2x + 3$. Déterminer la position relative de $\mathscr{C}_f$ et de la droite $\mathscr{D}$ d'équation $y = 2x - 1$.
Exercice 7
Soit $f(x) = -x^2 + 5x - 7$ et $g(x) = -x^2 - x + 5$. Étudier la position relative de $\mathscr{C}_f$ et $\mathscr{C}_g$.






