Variation et encadrement
Ici, vous trouverez une série d'exercices conçus pour vous aider à maîtriser les techniques d'étude des variations de fonctions et d'encadrement de leurs valeurs. Ces compétences sont essentielles pour l'analyse de fonctions et la résolution de problèmes en mathématiques.
Revoyons ensemble les points essentiels sur Variation et encadrement avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Dérivée et variations : le lien fondamental
Théorème clé : Signe de la dérivée et variations.
Pour une fonction $f$ dérivable sur un intervalle $I$ :
• Si, pour tout $x \in I$, $f'(x) > 0$, alors $f$ est strictement croissante sur $I$.
• Si, pour tout $x \in I$, $f'(x) < 0$, alors $f$ est strictement décroissante sur $I$.
• Si, pour tout $x \in I$, $f'(x) = 0$, alors $f$ est constante sur $I$.
L'étude des variations de $f$ se ramène donc à l'analyse du signe de sa dérivée $f'$.
Méthodologie :
1. Calculer la dérivée $f'(x)$.
2. Résoudre l'équation $f'(x) = 0$ pour trouver les points critiques.
3. Étudier le signe de $f'(x)$ sur les intervalles délimités par ces points critiques.
4. Dresser le tableau de variations, incluant les intervalles de croissance, décroissance et les extrema locaux.
2. Extrema locaux : maximums et minimums "près de chez soi"
Définitions : Maximum et Minimum Locaux.
• $f$ a un maximum local en $x_0$ si, autour de $x_0$, les valeurs de $f(x)$ sont inférieures ou égales à $f(x_0)$.
• $f$ a un minimum local en $x_0$ si, autour de $x_0$, les valeurs de $f(x)$ sont supérieures ou égales à $f(x_0)$.
Condition nécessaire : Dérivée nulle aux extrema locaux.
Si $f$ est dérivable en $x_0$ et présente un extremum local en $x_0$, alors $f'(x_0) = 0$.
Critère du changement de signe de la dérivée pour identifier la nature de l'extremum :
• Si $f'(x)$ passe de positive à négative en $x_0$, alors $f$ a un maximum local en $x_0$.
• Si $f'(x)$ passe de négative à positive en $x_0$, alors $f$ a un minimum local en $x_0$.
• Si $f'(x)$ ne change pas de signe en $x_0$, il n'y a pas d'extremum local (mais potentiellement un point d'inflexion).
3. Encadrement de fonctions : borner les valeurs
Exploiter les variations pour encadrer $f(x)$.
L'étude des variations de $f$ sur un intervalle $[a, b]$ permet d'identifier son minimum ($m$) et maximum ($M$) sur cet intervalle. On obtient alors l'encadrement :
Pour tout $x \in [a, b]$, $m \leq f(x) \leq M$.
Cas d'une fonction monotone sur $[a, b]$ :
• Si $f$ est croissante sur $[a, b]$, alors pour tout $x \in [a, b]$, $f(a) \leq f(x) \leq f(b)$.
• Si $f$ est décroissante sur $[a, b]$, alors pour tout $x \in [a, b]$, $f(b) \leq f(x) \leq f(a)$.
Ces encadrements sont précieux pour résoudre des inégalités et estimer des valeurs de fonctions.
4. Fonctions de référence : leurs variations à connaître
Récapitulatif des variations des fonctions usuelles.
• Fonction affine $f(x) = mx + p$ : Croissante si $m > 0$, décroissante si $m < 0$, constante si $m = 0$.
• Fonction carré $f(x) = x^2$ : Décroissante sur $]-\infty, 0]$, croissante sur $[0, +\infty[$.
• Fonction cube $f(x) = x^3$ : Strictement croissante sur $\mathbb{R}$.
• Fonction inverse $f(x) = \frac{1}{x}$ : Strictement décroissante sur $]-\infty, 0[$ et sur $]0, +\infty[$.
• Fonction racine carrée $f(x) = \sqrt{x}$ : Strictement croissante sur $[0, +\infty[$.
Ces fonctions de base servent de briques élémentaires pour l'étude de fonctions plus complexes.
Prêt ? 💪 Passons aux exercices pour mettre ces rappels en pratique !
Exercice 1
Soit $f$ la fonction définie et dérivable sur $\mathbb{R}$ par $f(x) = -4x + 9$. Étudier les variations de la fonction $f$.
Exercice 2
Soit $f$ la fonction définie et dérivable sur $\mathbb{R}$ par $f(x) = 2x² – 5x + 1$. Étudier les variations de la fonction $f$.
Exercice 3
Soit $f$ la fonction définie et dérivable sur $\mathbb{R}$ par $f(x) = 2x³ – 3x² + 4x$. Étudier les variations de la fonction $f$.
Exercice 4
Soit $f$ la fonction définie et dérivable sur $\mathbb{R}$ par $f(x) = x³/3 - 2x² + 5x + 1$. Étudier les variations de la fonction $f$.
Exercice 5
Soit $f$ la fonction définie et dérivable sur $]-\infty; 1/5[ \cup ]1/5; +∞[$ par $f(x) = \frac{3x+1}{5x-1}$. Étudier les variations de la fonction $f$.
Exercice 6
On considère la fonction $f$ définie et dérivable sur $\mathbb{R}$ dont la représentation graphique de sa fonction dérivée $f'$ est donnée ci-contre. En déduire les variations de la fonction $f$.
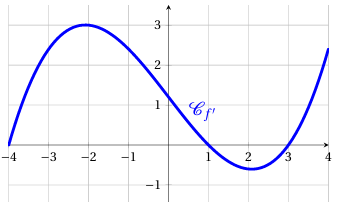
Exercice 7
On considère la fonction $g$ définie et dérivable sur $\mathbb{R}$ dont la représentation graphique est donnée ci-dessous. En déduire le tableau de signes de sa fonction dérivée $g'$.
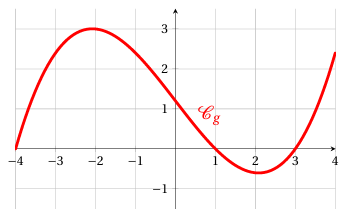
Exercice 7
On considère la fonction $g$ définie et dérivable sur $\mathbb{R}$ dont la représentation graphique est donnée ci-dessous. En déduire le tableau de signes de sa fonction dérivée $g'$.

Exercice 8
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = x³ – 3x² + mx$ où $m$ est un réel. Pour quelles valeurs de $m$ la fonction $f$ est-elle strictement croissante sur $\mathbb{R}$?
Exercice 9
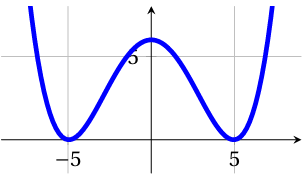
On a tracé ci-contre la courbe $C_f$ représentative
de la fonction $f$ définie sur $\mathbb{R}$ par $f (x) = \frac{x⁴}{100} - \frac{49x²}{100} + 6$.
Cette fonction semble toujours positive sur $\mathbb{R}$.
Confirmer ou infirmer cette conjecture par un calcul.
Exercice 10
Soit $f$ une fonction dérivable sur $\mathbb{R}$ et $f'$ sa dérivée. On donne le tableau de signes de $f'$.

La fonction $f$ admet-elle un extremum local? Si oui, est-ce un maximum ou un minimum?
Exercice 11
Soit $g$ une fonction dérivable sur $\mathbb{R}$ et $g'$ sa dérivée. On donne le tableau de signes de $g'$.

La fonction $g$ admet-elle un extremum local? Si oui, est-ce un maximum ou un minimum?
Exercice 12
Soit $h$ une fonction dérivable sur $\mathbb{R}$ et $h'$ sa dérivée. On donne le tableau de signes de $h'$.

La fonction $h$ admet-elle un minimum local? Si oui, en quelle valeur?
La fonction $h$ admet-elle un maximum local? Si oui, en quelle valeur?
Exercice 13
Soit $g$ la fonction définie sur $\mathbb{R}$ par $g(x) = −4x³ +9x$.
Justifier que $g$ est dérivable sur $\mathbb{R}$ et calculer $g'(x)$ pour tout réel $x$
Dresser le tableau de signes de $g'(x)$ sur $\mathbb{R}$.
En déduire que $g$ admet un maximum local en une valeur que l'on déterminera et un minimum local en une autre valeur que l'on déterminera.
Exercice 14
Une entreprise fabrique et vend des montres, entre 2 et 24 par jour. Soit $x$ le nombre de montres produites et vendues. Le coût journalier de fabrication est $C(x) = x² − 4x + 169$ euros. Le coût unitaire moyen est $C_m(x) = \frac{C(x)}{x}$.
Intervalle $I$ pour $x$?
Montrer que $C_m (x) = x −4+ \frac{169}{x}$ sur $I$.
Justifier la dérivabilité de $C_m$ sur $I$ et calculer $C'_m(x)$.
Tableau de signes de $C'_m (x)$ sur $I$.
Nombre de montres pour un coût moyen minimal.
Exercice 15
Soit un segment $[AB]$ de longueur 10 et $M \in [AB]$. On construit deux carrés $AMNP$ et $MBCD$ du même côté de $[AB]$. On pose $AM = x$ et on étudie l'aire totale des deux carrés.
Intervalle $I$ pour $x = AM$?
Schéma.
Montrer que l'aire totale est $f(x) = 2x² – 20x + 100$ pour $x \in I$.
Dérivabilité de $f$ sur $I$ et $f'(x)$.
Variations de $f$ sur $I$ et valeur de $x$ minimisant l'aire.
Exercice 16
Une coopérative produit du jus de pomme, entre 0 et 200 litres. Coût de production pour $x$ dizaines de litres : $C(x) = x² − x + 10$ euros. Vente : 19€ la dizaine de litres.
Domaine de définition de $C$?
Recette $R(x)$ pour $x$ dizaines de litres?
Bénéfice $B(x) = R(x) – C(x)$. Montrer que $B(x) = -x² + 20x - 10$ sur $[0;20]$.
Variations de $B$ sur $[0;20]$.
Production pour bénéfice maximum (en litres).
Exercice 17
Une entreprise produit $x$ objets par jour, vendus 100€ chacun. Coût de production unitaire : $U(x) = x−10+ \frac{900}{x}$ pour $ I = [10;100]$.
-
Étudier $U$ sur $I$ et tracer sa courbe $\mathscr{C}$ (unités : 1cm pour 5 objets et 1cm pour 10 €).
Production pour coût unitaire minimal? Bénéfice de l'entreprise?
Graphiquement, nombre d'objets pour $U(x) \leq 80$ € ?
Partie B: Étude du bénéfice
Montrer que le bénéfice global est $B(x) = −x² + 110x – 900$.
Variations de $B(x)$.
Production pour bénéfice maximal et bénéfice maximal?
Exercice 18
Boîte fermée de volume 1dm³ en forme de parallélépipède rectangle de hauteur $y$ et base carrée de côté $x > 0$.
Justifier que $y = 1/x²$
Aire totale $S(x) = 2x² + 4/x$
Montrer que $S' (x) = \frac{4(x³ - 1)}{x²}$ pour $x > 0$.
-
Variations de $S$ sur $\mathbb{R}^*_+$.
Dimensions de la boîte d'aire minimale.
Exercice 19
Mobile sur axe $[Ox)$. Position à l'instant $x$ (en s) : $f(x) = \frac{1}{3}x³ - 3x² + 9x$ (en cm), pour $x \in [0; 6]$.
Variations de $f$ sur $[0; 6]$
Mouvement du mobile.
Vitesse instantanée $v(x) = f'(x)$ en cm.s⁻¹.
Vitesse initiale?
Instants où vitesse $< 1cm.s⁻¹$?
Exercice 20
Variation et encadrement
Exercice 20
Soient $x < y < 0$. Dire si chaque inégalité est vraie ou fausse (justifier).
$x² > y²$
$1/x > 1/y$
$x/3 > y/3$
$x³ < y³$
$-y < -x$
Exercice 21
Démontrer que si $3 < x < 5$ alors $0 \leq (3 −x)² \leq 4$.













