Exercices : Matrices - Terminale Maths expertes

À Savoir : Rappels de Cours et Exemples Développés pour Maîtriser les Matrices.

1. Définition et Opérations de Base

Bonjour à tous ! Commençons par le début : qu'est-ce qu'une matrice ? Imaginez un tableau bien organisé de nombres. En Terminale, on se concentre surtout sur les matrices carrées, c'est-à-dire celles qui ont autant de lignes que de colonnes, et avec des nombres réels à l'intérieur. C'est notre outil principal pour manipuler des systèmes linéaires et bien plus !

Les opérations de base, c'est comme avec les nombres, mais adaptées aux matrices :

- Addition et Soustraction : Très simple ! On additionne (ou soustrait) les éléments qui se trouvent à la même position dans les matrices. Attention : On ne peut le faire que si les matrices ont exactement la même taille (même nombre de lignes et de colonnes). C'est comme comparer des pommes avec des pommes !

Exemple simple : Soient $A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ et $B = \begin{pmatrix} 5 & -1 \\ 0 & 2 \end{pmatrix}$. Alors, $$A + B = \begin{pmatrix} 1+5 & 2+(-1) \\ 3+0 & 4+2 \end{pmatrix} = \begin{pmatrix} 6 & 1 \\ 3 & 6 \end{pmatrix}$$

- Multiplication par un scalaire : Un scalaire, c'est juste un nombre réel (comme 2, -3, 0.5...). Multiplier une matrice par un scalaire, c'est multiplier chaque élément de la matrice par ce nombre. C'est comme agrandir ou rétrécir toute la matrice uniformément.

Exemple : Si $A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ et $\lambda = 3$, alors $$\lambda A = 3 \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} = \begin{pmatrix} 3\times1 & 3\times2 \\ 3\times3 & 3\times4 \end{pmatrix} = \begin{pmatrix} 3 & 6 \\ 9 & 12 \end{pmatrix}$$

- Produit matriciel : Là, ça devient un peu plus intéressant ! Pour multiplier deux matrices $A$ et $B$, il faut que le nombre de colonnes de $A$ soit égal au nombre de lignes de $B$. Le résultat $AB$ aura autant de lignes que $A$ et autant de colonnes que $B$. Pour trouver l'élément à la position $(i, j)$ dans $AB$, on prend la $i$-ème ligne de $A$ et la $j$-ème colonne de $B$, on multiplie les éléments correspondants et on additionne le tout. Important : En général, $AB \neq BA$. L'ordre compte énormément dans le produit matriciel ! On dit que le produit matriciel n'est pas commutatif.

Conseil Pratique : Visualisez bien les lignes de la première matrice qui "rencontrent" les colonnes de la deuxième. C'est la clé pour ne pas se tromper dans le produit matriciel !

Exemple de Produit Matriciel :

Soient $A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ et $B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}$. Alors, $$AB = \begin{pmatrix} (1\times5 + 2\times7) & (1\times6 + 2\times8) \\ (3\times5 + 4\times7) & (3\times6 + 4\times8) \end{pmatrix} = \begin{pmatrix} 19 & 22 \\ 43 & 50 \end{pmatrix}$$

Et si on essayait $BA$ ? $$BA = \begin{pmatrix} (5\times1 + 6\times3) & (5\times2 + 6\times4) \\ (7\times1 + 8\times3) & (7\times2 + 8\times4) \end{pmatrix} = \begin{pmatrix} 23 & 34 \\ 31 & 46 \end{pmatrix}$$ On voit bien que $AB \neq BA$ !

2. Inversibilité d'une Matrice et Déterminant

Maintenant, parlons d'inversibilité. Une matrice carrée $A$ est dite inversible si on peut trouver une autre matrice, qu'on appelle son inverse et qu'on note $A^{-1}$, telle que lorsqu'on les multiplie (dans les deux sens !), on obtient la matrice identité $I_n$. La matrice identité, c'est l'équivalent du nombre 1 pour les matrices : elle a des 1 sur la diagonale et des 0 partout ailleurs. Donc, on doit avoir : $$AA^{-1} = A^{-1}A = I_n$$

Mais comment savoir si une matrice est inversible et comment calculer son inverse ?

- Avec le Déterminant : Le déterminant, c'est un nombre qu'on associe à chaque matrice carrée. Pour une matrice 2x2 $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$, le déterminant est donné par $\det(A) = ad - bc$. Et la règle d'or : une matrice carrée $A$ est inversible si et seulement si son déterminant $\det(A)$ est différent de zéro. C'est un test très rapide pour savoir si on peut inverser une matrice !

Exemple : $A = \begin{pmatrix} 2 & 3 \\ 4 & 5 \end{pmatrix}$, $\det(A) = (2\times5) - (3\times4) = 10 - 12 = -2$. Comme $\det(A) = -2 \neq 0$, la matrice $A$ est inversible.

- Règle de Sarrus (pour les matrices 3x3) : Pour les matrices 3x3, on a une méthode pratique pour calculer le déterminant : la règle de Sarrus. Soit une matrice $A = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}$. On recopie les deux premières colonnes à droite de la matrice : $$\begin{pmatrix} a & b & c & a & b \\ d & e & f & d & e \\ g & h & i & g & h \end{pmatrix}$$ Puis, on calcule la somme des produits des diagonales descendantes et on soustrait la somme des produits des diagonales montantes :

$$\det(A) = (aei + bfg + cdh) - (ceg + afh + bdi)$$

Exemple avec Sarrus : Calculons le déterminant de $M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$. $$\det(M) = (1\times5\times9 + 2\times6\times7 + 3\times4\times8) - (3\times5\times7 + 1\times6\times8 + 2\times4\times9)$$ $$\det(M) = (45 + 84 + 96) - (105 + 48 + 72) = 225 - 225 = 0$$ Comme le déterminant est 0, la matrice $M$ n'est pas inversible.

Conseil Pratique : La règle de Sarrus est super pour les matrices 3x3, mais elle ne fonctionne pas pour les matrices plus grandes ! Pour les matrices plus grandes, il faut utiliser d'autres méthodes comme le développement par cofacteurs ou la méthode du pivot de Gauss.

- Méthode des cofacteurs (ou développement par mineurs) : Cette méthode est plus générale que la règle de Sarrus et fonctionne pour les matrices carrées de toute taille. Elle repose sur le développement du déterminant en utilisant les cofacteurs.

Mineur et Cofacteur :

Le mineur

Le cofacteur

Développement par cofacteurs : Le déterminant d'une matrice $A$ peut être calculé en choisissant une ligne ou une colonne, puis en sommant les produits des éléments de cette ligne (ou colonne) par leurs cofacteurs correspondants.

Développement par rapport à la $i$-ème ligne : $$\det(A) = \sum_{j=1}^{n} a_{ij} C_{ij} = a_{i1}C_{i1} + a_{i2}C_{i2} + \cdots + a_{in}C_{in}$$

Développement par rapport à la $j$-ème colonne : $$\det(A) = \sum_{i=1}^{n} a_{ij} C_{ij} = a_{1j}C_{1j} + a_{2j}C_{2j} + \cdots + a_{nj}C_{nj}$$

Exemple avec les cofacteurs : Calculons le déterminant de $M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$ en utilisant le développement par cofacteurs le long de la première ligne (i=1).

Pour $a_{11} = 1$:

Pour $a_{12} = 2$:

Pour $a_{13} = 3$:

Donc, $\det(M) = a_{11}C_{11} + a_{12}C_{12} + a_{13}C_{13} = (1 \times -3) + (2 \times 6) + (3 \times -3) = -3 + 12 - 9 = 0$.

Conseils Pratiques :

La méthode des cofacteurs fonctionne pour les matrices de toute taille

Pour les matrices de grande taille, le développement par cofacteurs peut devenir rapidement calculatoirement intensif

Pour les matrices de très grande taille, ou pour des calculs numériques, d'autres méthodes comme la méthode du pivot de Gauss sont souvent plus efficaces.

Pour les matrices 3x3, la règle de Sarrus est généralement plus rapide et plus simple que le développement par cofacteurs, si elle est applicable.

- Méthode du Pivot de Gauss : C'est une méthode plus générale et systématique pour inverser une matrice (et aussi pour résoudre des systèmes linéaires). On la verra surtout dans les exercices, mais sachez qu'elle est très puissante !

- Polynôme Annulateur : C'est une technique un peu plus avancée. Si on trouve un polynôme $P(X)$ tel que $P(A) = 0$ (la matrice nulle) et que ce polynôme a un terme constant non nul, alors on peut montrer que $A$ est inversible et même trouver une formule pour $A^{-1}$ à partir de $P(A) = 0$.

Exemple d'Inversion avec un Polynôme Annulateur : Supposons qu'on sache que pour une matrice $A$, on a $A^2 - 3A + 2I = 0$. Alors, on peut réécrire cette équation comme $2I = 3A - A^2 = A(3I - A)$. En divisant par 2, on obtient $I = A \left( \frac{1}{2}(3I - A) \right)$. Donc, par définition de l'inverse, on a $A^{-1} = \frac{1}{2}(3I - A)$. C'est une manière élégante de trouver l'inverse sans calculs compliqués !

Conseil Pratique : Le déterminant est votre ami pour vérifier rapidement l'inversibilité. Le pivot de Gauss est la méthode robuste pour calculer l'inverse en pratique, et le polynôme annulateur est une astuce à connaître pour certains cas particuliers, souvent dans les exercices théoriques.

3. Puissances de Matrices : Techniques de Calcul Malin

Calculer $A^n$, c'est multiplier $A$ par elle-même $n$ fois. Si $n$ est grand, faire les multiplications directement peut être très long et fastidieux ! Heureusement, il y a des techniques plus intelligentes :

- Récurrence : Parfois, en calculant les premières puissances $A^2, A^3, \dots$, on remarque un motif, une formule générale pour $A^n$. On peut alors prouver cette formule par récurrence. C'est une méthode puissante si on arrive à "voir" le motif !

Conseil Pratique : N'hésitez pas à calculer $A^2$, $A^3$ à la main pour les petits $n$. Souvent, la structure de la matrice $A^n$ devient claire après quelques itérations.

Exemple simple avec récurrence : Soit $D = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}$ une matrice diagonale. Calculons les premières puissances : $D^2 = \begin{pmatrix} 4 & 0 \\ 0 & 9 \end{pmatrix}$, $D^3 = \begin{pmatrix} 8 & 0 \\ 0 & 27 \end{pmatrix}$. On conjecture que $D^n = \begin{pmatrix} 2^n & 0 \\ 0 & 3^n \end{pmatrix}$. On peut facilement prouver cette formule par récurrence.

- Binôme de Newton : Vous connaissez le binôme $(a+b)^n = \sum_{k=0}^n \binom{n}{k} a^{n-k} b^k$. Il existe une formule similaire pour les matrices : $(B + C)^n = \sum_{k=0}^n \binom{n}{k} B^{n-k} C^k$. Attention : Cette formule ne marche que si les matrices $B$ et $C$ commutent, c'est-à-dire si $BC = CB$. C'est particulièrement utile si on peut écrire $A = I + B$ où $B$ est une matrice "simple" comme une matrice nilpotente (voir section suivante) ou si $B$ commute avec $I$ (ce qui est toujours le cas !).

Exemple avec Binôme de Newton : Soit $A = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}$. On peut écrire $A = I + B$ avec $I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ et $B = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}$. Comme $IB = BI = B$, on peut appliquer le binôme de Newton : $$A^n = (I+B)^n = \binom{n}{0}I^n + \binom{n}{1}I^{n-1}B + \binom{n}{2}I^{n-2}B^2 + \dots + \binom{n}{n}B^n$$ Or, on remarque que $B^2 = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = 0$. Donc, $B^2 = B^3 = \dots = B^n = 0$ pour $n \geq 2$. La formule se simplifie énormément : $$A^n = I + nB = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} + n \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 1 & n \\ 0 & 1 \end{pmatrix}$$ Calculer $A^n$ devient très facile !

- Polynôme Annulateur et Division Euclidienne : Encore une technique plus avancée, mais très efficace ! Si on connaît un polynôme annulateur $P(X)$ de $A$ (tel que $P(A) = 0$), on peut utiliser la division euclidienne de $X^n$ par $P(X)$. Si on écrit $X^n = Q(X)P(X) + R(X)$ avec le degré de $R(X)$ plus petit que le degré de $P(X)$, alors on a $A^n = R(A)$. Ça permet d'exprimer $A^n$ comme une combinaison linéaire de puissances inférieures de $A$. C'est très utile quand on a des polynômes annulateurs simples (comme $X^2 - 3X + 2$ par exemple).

Conseil Pratique : Pour les puissances de matrices, commencez toujours par regarder si vous pouvez utiliser la récurrence ou le binôme de Newton. Le polynôme annulateur est une technique plus sophistiquée, mais très puissante pour les cas plus complexes.

4. Matrices Spéciales : Nilpotentes, Stochastiques, et de Rotation

Il existe des familles de matrices qui ont des propriétés particulières et qui sont très utiles dans différents contextes :

- Matrices Nilpotentes : Une matrice $A$ est dite nilpotente s'il existe un entier $p \geq 1$ (appelé indice de nilpotence) tel que $A^p = 0$. Ces matrices ont des valeurs propres toutes nulles (leur spectre propre est réduit à $\{0\}$). Elles sont très pratiques car elles simplifient le calcul de $(I - A)^{-1}$ en utilisant la série géométrique matricielle (qui devient une somme finie car les puissances de $A$ finissent par s'annuler).

Exemple : La matrice $B = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}$ est nilpotente d'indice 2 car $B^2 = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} = 0$. Donc, pour cette matrice, $(I - B)^{-1} = I + B = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}$. Beaucoup plus simple que d'inverser directement $(I-B)$ !

- Matrices Stochastiques : Ce sont des matrices carrées dont tous les coefficients sont positifs ou nuls et dont la somme des coefficients de chaque ligne est égale à 1. Elles sont utilisées pour modéliser des systèmes probabilistes où l'état total du système est conservé (par exemple, des chaînes de Markov). Les matrices bistochastiques ont en plus la propriété que la somme des coefficients de chaque colonne est aussi égale à 1. Elles sont liées aux permutations et au théorème de Birkhoff-Von Neumann (mais ça, c'est pour plus tard !).

Exemple : $S = \begin{pmatrix} 0.5 & 0.5 \\ 0.3 & 0.7 \end{pmatrix}$ est une matrice stochastique car tous les coefficients sont positifs et $0.5 + 0.5 = 1$ et $0.3 + 0.7 = 1$.

- Matrices de Rotation 2D : Elles servent à représenter des rotations d'angle $\theta$ autour de l'origine dans le plan. Elles ont une forme très précise :

$$ R(\theta) = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} $$

Leur déterminant est toujours égal à 1, ce qui garantit que les rotations conservent les aires et les orientations. Si vous multipliez un vecteur par $R(\theta)$, vous faites tourner ce vecteur d'un angle $\theta$ dans le sens trigonométrique.

Exemple : Pour une rotation de 90 degrés ($\theta = \pi/2$), on a $\cos(\pi/2) = 0$ et $\sin(\pi/2) = 1$. Donc, la matrice de rotation est $R(\pi/2) = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$. Si on applique cette matrice au vecteur $\begin{pmatrix} 1 \\ 0 \end{pmatrix}$ (le vecteur unitaire horizontal), on obtient $R(\pi/2) \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$ (le vecteur unitaire vertical), ce qui correspond bien à une rotation de 90 degrés !

Conseil Pratique : Retenez bien ces familles de matrices spéciales. Elles reviennent souvent dans les exercices et les problèmes, et comprendre leurs propriétés vous fera gagner beaucoup de temps !

C'est noté ? 💪 Maintenant, place aux exercices ! Entraînez-vous bien, c'est en pratiquant qu'on devient fort en matrices ! Bonne chance !

Exercice 1 - Matrices Commutantes

Soient $a$ et $b$ deux nombres réels non nuls. On considère la matrice $A=\left( \begin{array}{cc} a & b\\ 0 &a \end{array} \right).$ Trouver toutes les matrices $B\in\mathcal M_2(\mathbb R)$ qui commutent avec $A$, c'est-à-dire telles que $AB=BA$. Décrire la forme générale de ces matrices $B$.

Correction :

Pour résoudre cet exercice, nous allons chercher la forme générale d'une matrice $B = \begin{pmatrix} c & d \\ e & f \end{pmatrix}$ qui commute avec la matrice $A = \begin{pmatrix} a & b\\ 0 &a \end{pmatrix}$. La condition de commutation est que le produit matriciel $AB$ soit égal au produit matriciel $BA$.

Calculons d'abord le produit $AB$ : $$ AB = \begin{pmatrix} a & b\\ 0 &a \end{pmatrix} \begin{pmatrix} c & d\\ e &f \end{pmatrix} = \begin{pmatrix} ac+be & ad+bf\\ ae &af \end{pmatrix} $$

Ensuite, calculons le produit $BA$ : $$ BA = \begin{pmatrix} c & d\\ e &f \end{pmatrix} \begin{pmatrix} a & b\\ 0 &a \end{pmatrix} = \begin{pmatrix} ac & bc+ad\\ ae &be+af \end{pmatrix} $$

Pour que $AB = BA$, les matrices doivent être égales terme à terme. Nous devons donc identifier les coefficients correspondants : $$ \begin{pmatrix} ac+be & ad+bf\\ ae &af \end{pmatrix} = \begin{pmatrix} ac & bc+ad\\ ae &be+af \end{pmatrix} $$

Cette égalité matricielle nous donne un système d'équations en comparant les coefficients : $$ \begin{cases} ac+be = ac \\ ad+bf = bc+ad \\ ae = ae \\ af = be+af \end{cases} $$

Simplifions ce système d'équations : $$ \begin{cases} be = 0 & \text{ (de la première équation)} \\ bf = bc & \text{ (de la deuxième équation, après simplification de } ad \text{ de chaque côté)} \\ ae = ae & \text{ (toujours vrai, ne donne pas de nouvelle information)} \\ af = be+af & \text{ (de la quatrième équation)} \end{cases} \Leftrightarrow \begin{cases} be = 0 \\ bf = bc \\ be = 0 \end{cases} $$ Les équations 1 et 4 sont identiques, et la troisième est toujours vraie. Nous nous retrouvons donc avec seulement deux équations significatives : $$ \begin{cases} be = 0 \\ bf = bc \end{cases} $$

Puisque l'énoncé précise que $b \neq 0$, nous pouvons déduire de la première équation $be = 0$ que $e = 0$.

En utilisant $e = 0$ dans la deuxième équation $bf = bc$, nous obtenons $bf = bc$. Puisque $b \neq 0$, nous pouvons simplifier par $b$ pour obtenir $f = c$.

Ainsi, nous avons trouvé que pour que $B$ commute avec $A$, il faut que $e = 0$ et $f = c$. Les coefficients $c$ et $d$ restent libres (peuvent être n'importe quel réel).

Par conséquent, les matrices $B$ qui commutent avec $A$ sont de la forme : $$ B = \begin{pmatrix} c & d\\ 0 &c \end{pmatrix}, \quad \text{où } c, d \in \mathbb{R}. $$

Exercice 2 - Matrices Annulateurs et Inversibilité

On considère les matrices $A=\left(\begin{array}{ccc} 1&0&0\\ 0&1&1\\ 3&1&1\end{array}\right)$, $B=\left(\begin{array}{ccc} 1&1&1\\ 0&1&0\\ 1&0&0\end{array}\right)$ et $C=\left(\begin{array}{ccc} 1&1&1\\ 1&2&1\\ 0&-1&-1\end{array}\right)$.

Calculer les produits matriciels $AB$ et $AC$. Que remarquez-vous ?
La matrice $A$ est-elle inversible ? Justifier votre réponse.
Trouver toutes les matrices $F\in\mathcal M_3(\mathbb R)$ telles que $AF=0$, où $0$ désigne la matrice nulle 3x3.

Correction :

Calcul de $AB$ :
$$ AB = \left(\begin{array}{ccc} 1&0&0\\ 0&1&1\\ 3&1&1\end{array}\right) \left(\begin{array}{ccc} 1&1&1\\ 0&1&0\\ 1&0&0\end{array}\right) $$ $$ AB = \left(\begin{array}{ccc} (1\times1+0\times0+0\times1)&(1\times1+0\times1+0\times0)&(1\times1+0\times0+0\times0)\\ (0\times1+1\times0+1\times1)&(0\times1+1\times1+1\times0)&(0\times1+1\times0+1\times0)\\ (3\times1+1\times0+1\times1)&(3\times1+1\times1+1\times0)&(3\times1+1\times0+1\times0) \end{array}\right) = \left(\begin{array}{ccc} 1&1&1\\ 1&1&0\\ 4&4&3 \end{array}\right) $$
Calcul de $AC$ :
$$ AC = \left(\begin{array}{ccc} 1&0&0\\ 0&1&1\\ 3&1&1\end{array}\right) \left(\begin{array}{ccc} 1&1&1\\ 1&2&1\\ 0&-1&-1\end{array}\right)$$ $$ AC = \left(\begin{array}{ccc} (1\times1+0\times1+0\times0)&(1\times1+0\times2+0\times(-1))&(1\times1+0\times1+0\times(-1))\\ (0\times1+1\times1+1\times0)&(0\times1+1\times2+1\times(-1))&(0\times1+1\times1+1\times(-1))\\ (3\times1+1\times1+1\times0)&(3\times1+1\times2+1\times(-1))&(3\times1+1\times1+1\times(-1)) \end{array}\right)$$ $$ AC = \left(\begin{array}{ccc} 1&1&1\\ 1&1&0\\ 4&4&3 \end{array}\right) $$
Remarque : On observe que $AB = AC$.
Inversibilité de $A$ :

Si la matrice $A$ était inversible, alors l'égalité $AB = AC$ impliquerait $B = C$ (en multipliant à gauche par $A^{-1}$ : $A^{-1}AB = A^{-1}AC \Rightarrow IB = IC \Rightarrow B = C$).

Or, en comparant les matrices $B$ et $C$, on constate que $B \neq C$ (par exemple, le coefficient en position (2,1) est 0 dans $B$ et 1 dans $C$).

Puisque $AB = AC$ mais $B \neq C$, nous arrivons à une contradiction si $A$ est inversible. Donc, la matrice $A$ n'est pas inversible.

Autre justification :

De $AB = AC$, on déduit $AB - AC = 0$, ce qui peut s'écrire $A(B-C) = 0$, où $0$ est la matrice nulle 3x3.

Calculons la matrice $B-C$ : $$ B-C = \left(\begin{array}{ccc} 1&1&1\\ 0&1&0\\ 1&0&0\end{array}\right) - \left(\begin{array}{ccc} 1&1&1\\ 1&2&1\\ 0&-1&-1\end{array}\right) = \left(\begin{array}{ccc} 0&0&0\\ -1&-1&1\\ 1&1&1\end{array}\right) $$ On observe que $B-C \neq 0$ (ce n'est pas la matrice nulle).

Nous avons donc trouvé une matrice non nulle $B-C$ telle que $A(B-C) = 0$. Si $A$ était inversible, on pourrait multiplier à gauche par $A^{-1}$ pour obtenir $A^{-1}A(B-C) = A^{-1}0$, ce qui donnerait $I(B-C) = 0$, soit $B-C = 0$, ce qui contredit le fait que $B-C \neq 0$. Par conséquent, $A$ n'est pas inversible.
Matrices $F$ telles que $AF=0$ :

Soit $F = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}$. Nous voulons résoudre l'équation matricielle $AF = 0$.

Calculons le produit $AF$ : $$ AF = \left(\begin{array}{ccc} 1&0&0\\ 0&1&1\\ 3&1&1\end{array}\right) \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}$$ $$ AF = \begin{pmatrix} (1\times a+0\times d+0\times g)&(1\times b+0\times e+0\times h)&(1\times c+0\times f+0\times i)\\ (0\times a+1\times d+1\times g)&(0\times b+1\times e+1\times h)&(0\times c+1\times f+1\times i)\\ (3\times a+1\times d+1\times g)&(3\times b+1\times e+1\times h)&(3\times c+1\times f+1\times i) \end{pmatrix}$$ $$ AF = \begin{pmatrix} a&b&c\\ d+g&e+h&f+i\\ 3a+d+g&3b+e+h&3c+f+i \end{pmatrix} $$

Pour que $AF = 0$, chaque coefficient de la matrice $AF$ doit être nul. Cela nous donne le système d'équations : $$ \begin{cases} a=0 \\ b=0 \\ c=0 \\ d+g=0 \\ e+h=0 \\ f+i=0 \\ 3a+d+g=0 \\ 3b+e+h=0 \\ 3c+f+i=0 \end{cases} $$

En utilisant les trois premières équations ($a=0, b=0, c=0$), les équations 7, 8, 9 deviennent $d+g=0, e+h=0, f+i=0$, qui sont identiques aux équations 4, 5, 6. On a donc le système simplifié : $$ \begin{cases} a=0 \\ b=0 \\ c=0 \\ d+g=0 \\ e+h=0 \\ f+i=0 \end{cases} \Leftrightarrow \begin{cases} a=0 \\ b=0 \\ c=0 \\ g=-d \\ h=-e \\ i=-f \end{cases} $$

Les solutions pour $F$ sont donc les matrices de la forme : $$ F = \begin{pmatrix} 0 & 0 & 0 \\ d & e & f \\ -d & -e & -f \end{pmatrix}, \quad \text{où } d, e, f \in \mathbb{R}. $$ Ici, $d, e, f$ sont des paramètres réels libres. Il y a donc une infinité de matrices $F$ telles que $AF=0$.

Exercice 3 - Produit Matriciel Non Commutatif

Trouver deux matrices carrées $A$ et $B$ d'ordre 2 ($\mathcal M_2({\mathbb R})$) telles que leur produit $AB$ soit la matrice nulle, mais que le produit $BA$ ne soit pas la matrice nulle. Justifier votre choix.

Correction :

Pour illustrer que le produit matriciel n'est pas commutatif (en général $AB \neq BA$), on cherche ici un exemple où $AB = 0$ (la matrice nulle) mais $BA \neq 0$.

Considérons les matrices suivantes, relativement simples : $$ A = \begin{pmatrix} 0&1\\ 0&0 \end{pmatrix} \quad \text{et} \quad B = \begin{pmatrix} 1&0\\ 0&0 \end{pmatrix} $$

Calculons le produit $AB$ : $$ AB = \begin{pmatrix} 0&1\\ 0&0 \end{pmatrix} \begin{pmatrix} 1&0\\ 0&0 \end{pmatrix} = \begin{pmatrix} (0\times1+1\times0)&(0\times0+1\times0)\\ (0\times1+0\times0)&(0\times0+0\times0) \end{pmatrix} = \begin{pmatrix} 0&0\\ 0&0 \end{pmatrix} = 0 $$ Ainsi, le produit $AB$ est bien la matrice nulle.

Calculons maintenant le produit $BA$ : $$ BA = \begin{pmatrix} 1&0\\ 0&0 \end{pmatrix} \begin{pmatrix} 0&1\\ 0&0 \end{pmatrix} = \begin{pmatrix} (1\times0+0\times0)&(1\times1+0\times0)\\ (0\times0+0\times0)&(0\times1+0\times0) \end{pmatrix} = \begin{pmatrix} 0&1\\ 0&0 \end{pmatrix} = A $$ On remarque que $BA = A$, et puisque $A \neq 0$, alors $BA \neq 0$.

Conclusion : Les matrices $A = \begin{pmatrix} 0&1\\ 0&0 \end{pmatrix}$ et $B = \begin{pmatrix} 1&0\\ 0&0 \end{pmatrix}$ sont un exemple de matrices carrées d'ordre 2 telles que $AB=0$ et $BA \neq 0$. Ceci illustre bien que le produit matriciel n'est pas commutatif.

Exercice 4 - Puissance $n$-ième d'une Matrice par Récurrence

On considère les matrices suivantes : $$A=\left(\begin{array}{cc} 1&-1\\ -1&1\\ \end{array}\right),\ B=\left(\begin{array}{cc} 1&1\\ 0&2\\ \end{array}\right).$$

Calculer $A^2$ et $A^3$. Conjecturer une formule pour $A^n$ pour tout entier $n\geq 1$, puis démontrer cette formule par récurrence.
Calculer $B^2$ et $B^3$. Conjecturer une formule pour $B^n$ pour tout entier $n\geq 1$, puis démontrer cette formule par récurrence.

Correction :

Calcul des premières puissances de $A$ :
$$ A^2 = \left(\begin{array}{cc} 1&-1\\ -1&1 \end{array}\right) \left(\begin{array}{cc} 1&-1\\ -1&1 \end{array}\right) = \left(\begin{array}{cc} (1\times1+(-1)\times(-1))&(1\times(-1)+(-1)\times1)\\ ((-1)\times1+1\times(-1))&((-1)\times(-1)+1\times1) \end{array}\right) = \left(\begin{array}{cc} 2&-2\\ -2&2 \end{array}\right) $$ On remarque que $A^2 = 2\left(\begin{array}{cc} 1&-1\\ -1&1 \end{array}\right) = 2A$. $$ A^3 = A^2 A = (2A) \cdot A = 2A^2 = 2(2A) = 4A = 2^2 A $$
Conjecture pour $A^n$ :

En observant $A^2 = 2A$ et $A^3 = 2^2 A$, on peut conjecturer que pour tout entier $n \geq 1$, $A^n = 2^{n-1}A$.

Démonstration par récurrence :

Initialisation : Pour $n=1$, la formule donne $A^1 = 2^{1-1}A = 2^0 A = 1 \cdot A = A$. La formule est donc vraie pour $n=1$.

Hérédité : Supposons que la formule soit vraie pour un certain entier $k \geq 1$, c'est-à-dire $A^k = 2^{k-1}A$. Montrons qu'elle est alors vraie pour $k+1$, c'est-à-dire $A^{k+1} = 2^{(k+1)-1}A = 2^k A$.

En utilisant l'hypothèse de récurrence, on a : $$ A^{k+1} = A^k \cdot A = (2^{k-1}A) \cdot A = 2^{k-1} (A \cdot A) = 2^{k-1} A^2 $$ Nous savons que $A^2 = 2A$, donc : $$ A^{k+1} = 2^{k-1} (2A) = (2^{k-1} \cdot 2) A = 2^k A $$ Ceci est bien la formule attendue pour le rang $k+1$. L'hérédité est donc démontrée.

Conclusion : Par le principe de récurrence, la formule $A^n = 2^{n-1}A$ est vraie pour tout entier $n \geq 1$. On peut aussi écrire : $$ A^n = 2^{n-1}A = 2^{n-1} \left(\begin{array}{cc} 1&-1\\ -1&1 \end{array}\right) = \begin{pmatrix} 2^{n-1} & -2^{n-1} \\ -2^{n-1} & 2^{n-1} \end{pmatrix}, \quad \text{pour } n \geq 1. $$
Calcul des premières puissances de $B$ :
$$ B^2 = \left(\begin{array}{cc} 1&1\\ 0&2 \end{array}\right) \left(\begin{array}{cc} 1&1\\ 0&2 \end{array}\right) = \left(\begin{array}{cc} (1\times1+1\times0)&(1\times1+1\times2)\\ (0\times1+2\times0)&(0\times1+2\times2) \end{array}\right) = \left(\begin{array}{cc} 1&3\\ 0&4 \end{array}\right) $$ $$ B^3 = B^2 B = \left(\begin{array}{cc} 1&3\\ 0&4 \end{array}\right) \left(\begin{array}{cc} 1&1\\ 0&2 \end{array}\right) = \left(\begin{array}{cc} (1\times1+3\times0)&(1\times1+3\times2)\\ (0\times1+4\times0)&(0\times1+4\times2) \end{array}\right) = \left(\begin{array}{cc} 1&7\\ 0&8 \end{array}\right) $$
Conjecture pour $B^n$ :

Observons les coefficients de $B^n$ pour $n=1, 2, 3$: $$ B^1 = \left(\begin{array}{cc} 1&1\\ 0&2 \end{array}\right), \quad B^2 = \left(\begin{array}{cc} 1&3\\ 0&4 \end{array}\right), \quad B^3 = \left(\begin{array}{cc} 1&7\\ 0&8 \end{array}\right) $$ On remarque que le coefficient en position (1,1) est toujours 1, le coefficient en position (2,1) est toujours 0, et le coefficient en position (2,2) est $2^n$. Pour le coefficient en position (1,2), on a 1, 3, 7, ce qui semble être de la forme $2^n - 1$. En effet, $2^1-1 = 1$, $2^2-1 = 3$, $2^3-1 = 7$.

On conjecture donc que pour tout entier $n \geq 1$, $B^n = \left(\begin{array}{cc} 1&2^n-1\\ 0&2^n \end{array}\right)$.

Démonstration par récurrence :

Initialisation : Pour $n=1$, la formule donne $B^1 = \left(\begin{array}{cc} 1&2^1-1\\ 0&2^1 \end{array}\right) = \left(\begin{array}{cc} 1&1\\ 0&2 \end{array}\right) = B$. La formule est donc vraie pour $n=1$.

Hérédité : Supposons que la formule soit vraie pour un certain entier $k \geq 1$, c'est-à-dire $B^k = \left(\begin{array}{cc} 1&2^k-1\\ 0&2^k \end{array}\right)$. Montrons qu'elle est alors vraie pour $k+1$, c'est-à-dire $B^{k+1} = \left(\begin{array}{cc} 1&2^{k+1}-1\\ 0&2^{k+1} \end{array}\right)$.

En utilisant l'hypothèse de récurrence, on a : $$ B^{k+1} = B^k \cdot B = \left(\begin{array}{cc} 1&2^k-1\\ 0&2^k \end{array}\right) \left(\begin{array}{cc} 1&1\\ 0&2 \end{array}\right) = \left(\begin{array}{cc} (1\times1+(2^k-1)\times0)&(1\times1+(2^k-1)\times2)\\ (0\times1+2^k\times0)&(0\times1+2^k\times2) \end{array}\right) $$ $$ B^{k+1} = \left(\begin{array}{cc} 1 & 1 + 2(2^k-1) \\ 0 & 2^{k+1} \end{array}\right) $$ Simplifions le coefficient (1,2) : $1 + 2(2^k-1) = 1 + 2^{k+1} - 2 = 2^{k+1} - 1$. Donc, $$ B^{k+1} = \left(\begin{array}{cc} 1 & 2^{k+1} - 1 \\ 0 & 2^{k+1} \end{array}\right) $$ Ceci est bien la formule attendue pour le rang $k+1$. L'hérédité est donc démontrée.

Conclusion : Par le principe de récurrence, la formule $B^n = \left(\begin{array}{cc} 1&2^n-1\\ 0&2^n \end{array}\right)$ est vraie pour tout entier $n \geq 1$.

Exercice 5 - Puissance $n$-ième et Binôme de Newton

Soit $$A=\left( \begin{array}{ccc} 1&1&0\\ 0&1&1\\ 0&0&1 \end{array}\right),\quad I=\left( \begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}\right)\textrm{ et } B=A-I.$$

Calculer les matrices $B$, $B^2$, $B^3$. Que remarquez-vous pour les puissances de $B$ ?
Exprimer $A$ en fonction de $I$ et $B$. Justifier pourquoi on peut utiliser la formule du binôme de Newton pour calculer $A^n$.
Calculer $A^n$ pour tout entier naturel $n$ en utilisant la formule du binôme de Newton.

Correction :

Calcul de $B$ :
$$ B = A-I = \left(\begin{array}{ccc} 1&1&0\\ 0&1&1\\ 0&0&1 \end{array}\right) - \left(\begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}\right) = \left(\begin{array}{ccc} 0&1&0\\ 0&0&1\\ 0&0&0 \end{array}\right) $$
Calcul de $B^2$ :
$$ B^2 = B \cdot B = \left(\begin{array}{ccc} 0&1&0\\ 0&0&1\\ 0&0&0 \end{array}\right) \left(\begin{array}{ccc} 0&1&0\\ 0&0&1\\ 0&0&0 \end{array}\right) $$ $$ B^2 = \left(\begin{array}{ccc} (0\times0+1\times0+0\times0)&(0\times1+1\times0+0\times0)&(0\times0+1\times1+0\times0)\\ (0\times0+0\times0+1\times0)&(0\times1+0\times0+1\times0)&(0\times0+0\times1+1\times0)\\ (0\times0+0\times0+0\times0)&(0\times1+0\times0+0\times0)&(0\times0+0\times1+0\times0) \end{array}\right) $$ $$ B^2 = \left(\begin{array}{ccc} 0&0&1\\ 0&0&0\\ 0&0&0 \end{array}\right) $$
Calcul de $B^3$ :
$$ B^3 = B^2 \cdot B = \left(\begin{array}{ccc} 0&0&1\\ 0&0&0\\ 0&0&0 \end{array}\right) \left(\begin{array}{ccc} 0&1&0\\ 0&0&1\\ 0&0&0 \end{array}\right) $$ $$ B^3 = \left(\begin{array}{ccc} (0\times0+0\times0+1\times0)&(0\times1+0\times0+1\times0)&(0\times0+0\times1+1\times0)\\ (0\times0+0\times0+0\times0)&(0\times1+0\times0+0\times0)&(0\times0+0\times1+0\times0)\\ (0\times0+0\times0+0\times0)&(0\times1+0\times0+0\times0)&(0\times0+0\times1+0\times0) \end{array}\right) $$ $$ B^3 = \left(\begin{array}{ccc} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array}\right) = 0 $$
Remarque : On observe que $B^3 = 0$ (matrice nulle). De plus, pour tout $k \geq 3$, on aura $B^k = B^{k-3} \cdot B^3 = B^{k-3} \cdot 0 = 0$. On dit que la matrice $B$ est nilpotente d'indice 3.
Expression de $A$ en fonction de $I$ et $B$ :

Par définition de $B$, nous avons $B = A - I$, donc en réarrangeant, on obtient $A = I + B$.

Justification de l'utilisation du binôme de Newton :

La formule du binôme de Newton pour $(X+Y)^n = \sum_{k=0}^n \binom{n}{k} X^{n-k} Y^k$ est valide si et seulement si les éléments $X$ et $Y$ commutent, c'est-à-dire $XY = YX$.

Dans notre cas, nous avons $A = I + B$. Nous devons vérifier si $I$ et $B$ commutent. Or, la matrice identité $I$ commute avec toute matrice carrée de même dimension. En particulier, $IB = BI = B$. Donc, $I$ et $B$ commutent. On peut donc appliquer la formule du binôme de Newton pour calculer $(I+B)^n = A^n$.
Calcul de $A^n$ avec le binôme de Newton :

En utilisant la formule du binôme de Newton et $A = I + B$, on a : $$ A^n = (I+B)^n = \sum_{k=0}^n \binom{n}{k} I^{n-k} B^k = \sum_{k=0}^n \binom{n}{k} B^k $$ car $I^{n-k} = I$ pour tout $k$. De plus, nous avons vu que $B^k = 0$ pour $k \geq 3$. Donc, la somme se réduit aux termes pour $k = 0, 1, 2$: $$ A^n = \binom{n}{0} B^0 + \binom{n}{1} B^1 + \binom{n}{2} B^2 $$ Rappelons que $B^0 = I$, $B^1 = B$, $B^2 = \begin{pmatrix} 0&0&1\\ 0&0&0\\ 0&0&0 \end{pmatrix}$, $\binom{n}{0} = 1$, $\binom{n}{1} = n$, $\binom{n}{2} = \frac{n(n-1)}{2}$. Donc, $$ A^n = 1 \cdot I + n \cdot B + \frac{n(n-1)}{2} B^2 = I + nB + \frac{n(n-1)}{2} B^2 $$

Exprimons $A^n$ en forme matricielle en substituant les expressions de $I$, $B$, $B^2$: $$ A^n = \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix} + n \begin{pmatrix} 0&1&0\\ 0&0&1\\ 0&0&0 \end{pmatrix} + \frac{n(n-1)}{2} \begin{pmatrix} 0&0&1\\ 0&0&0\\ 0&0&0 \end{pmatrix} = \begin{pmatrix} 1+0+0 & 0+n+0 & 0+0+\frac{n(n-1)}{2} \\ 0+0+0 & 1+0+0 & 0+n+0 \\ 0+0+0 & 0+0+0 & 1+0+0 \end{pmatrix} $$

Conclusion : La puissance $n$-ième de la matrice $A$ est donnée par : $$ A^n = \begin{pmatrix} 1&n&\frac{n(n-1)}{2}\\ 0&1&n\\ 0&0&1 \end{pmatrix}, \quad \text{pour tout entier naturel } n. $$

Exercice 6 - Puissance $n$-ième et Division Euclidienne de Polynômes

Pour un entier $n\geq 2$, déterminer le reste de la division euclidienne du polynôme $X^n$ par le polynôme $P(X) = X^2-3X+2$.
Soit $A=\begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix}$. Calculer $A^2-3A+2I_3$. En utilisant le résultat de la question 1, exprimer $A^n$ en fonction de $A$ et de la matrice identité $I_3$ pour $n\geq 2$.

Correction :

Division euclidienne de $X^n$ par $P(X) = X^2-3X+2$ :

Le diviseur est $P(X) = X^2-3X+2 = (X-1)(X-2)$. C'est un polynôme de degré 2. Le reste de la division euclidienne de $X^n$ par $P(X)$ sera donc un polynôme de degré au plus 1. Notons le reste $R_n(X) = a_nX+b_n$. Alors, par définition de la division euclidienne, il existe un polynôme quotient $Q_n(X)$ tel que : $$ X^n = (X^2-3X+2)Q_n(X) + R_n(X) = (X-1)(X-2)Q_n(X) + a_nX+b_n $$ Cette égalité est vraie pour tout $X$. En particulier, elle est vraie pour les racines de $P(X)$, qui sont $X=1$ et $X=2$.

Pour $X=1$ :

En substituant $X=1$ dans l'équation ci-dessus, on obtient : $$ 1^n = (1-1)(1-2)Q_n(1) + a_n(1)+b_n \Rightarrow 1 = 0 \cdot Q_n(1) + a_n+b_n \Rightarrow a_n+b_n = 1 $$

Pour $X=2$ :

En substituant $X=2$ dans l'équation, on obtient : $$ 2^n = (2-1)(2-2)Q_n(2) + a_n(2)+b_n \Rightarrow 2^n = (1)(0)Q_n(2) + 2a_n+b_n \Rightarrow 2a_n+b_n = 2^n $$

Nous avons donc un système de deux équations linéaires pour déterminer $a_n$ et $b_n$ : $$ \begin{cases} a_n+b_n = 1 \\ 2a_n+b_n = 2^n \end{cases} $$

Pour résoudre ce système, on peut soustraire la première équation de la seconde : $(2a_n+b_n) - (a_n+b_n) = 2^n - 1 \Rightarrow a_n = 2^n-1$. Ensuite, en utilisant la première équation, $b_n = 1-a_n = 1 - (2^n-1) = 1 - 2^n + 1 = 2 - 2^n$.

Conclusion pour la question 1 : Le reste de la division euclidienne de $X^n$ par $P(X) = X^2-3X+2$ est $R_n(X) = a_nX+b_n = (2^n-1)X + (2-2^n)$.
Calcul de $A^2-3A+2I_3$ :

Soit $A=\begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix}$. Calculons d'abord $A^2$: $$ A^2 = \begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix} \begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix} = \begin{pmatrix} (0-1-1)&(0+2+1)&(0-1-2)\\ (0-2-1)&(-1+4+1)&(1-2-2)\\ (0+1+2)&(1-2-2)&(-1+1+4) \end{pmatrix} $$ $$ A^2 = \begin{pmatrix} -2&3&-3\\ -3&4&-3\\ 3&-3&4 \end{pmatrix} $$

Maintenant, calculons $A^2-3A+2I_3$ : $$ A^2-3A+2I_3 = \begin{pmatrix} -2&3&-3\\ -3&4&-3\\ 3&-3&4 \end{pmatrix} - 3\begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix} + 2\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix} $$ $$ = \begin{pmatrix} -2-0+2 & 3-3+0 & -3+3+0 \\ -3+3+0 & 4-6+2 & -3+3+0 \\ 3-3+0 & -3+3+0 & 4-6+2 \end{pmatrix} = \begin{pmatrix} 0&0&0\\ 0&0&0\\ 0&0&0 \end{pmatrix} = 0_{3\times3} $$

Remarque importante : Pour la matrice $A$ donnée, on a bien $A^2-3A+2I_3 = 0$. Ceci signifie que $P(A) = 0$, où $P(X) = X^2-3X+2$. On dit que $P(X)$ est un polynôme annulateur de $A$.

Expression de $A^n$ en fonction de $A$ et $I_3$ :

Nous avons trouvé à la question 1 que $X^n = (X^2-3X+2)Q_n(X) + R_n(X)$, avec $R_n(X) = (2^n-1)X + (2-2^n)$. Puisque $P(A) = A^2-3A+2I_3 = 0$, on peut remplacer $X$ par $A$ dans l'équation de la division euclidienne. Le terme $(X^2-3X+2)Q_n(X)$ devient $(A^2-3A+2I_3)Q_n(A) = 0 \cdot Q_n(A) = 0$. Donc, $$ A^n = (A^2-3A+2I_3)Q_n(A) + R_n(A) = 0 + R_n(A) = R_n(A) $$

Ainsi, $A^n = R_n(A) = (2^n-1)A + (2-2^n)I_3$.

Conclusion pour la question 2 : Pour $n \geq 2$, on a $A^n = (2^n-1)A + (2-2^n)I_3$.

Exercice 7 - Système 3x3, Inversibilité et Pivot de Gauss

On considère le système d'équations linéaires suivant : $$ \begin{cases} x + 2y - z = 2 \\ 2x - y + 3z = -5 \\ -x + 3y + 2z = 7 \end{cases} $$

Écrire ce système d'équations sous la forme matricielle $AX = B$, où $A$ est une matrice carrée d'ordre 3, $X = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$ est le vecteur des inconnues, et $B$ est un vecteur colonne. Préciser les matrices $A$ et $B$.
Calculer le déterminant de la matrice $A$. La matrice $A$ est-elle inversible ? Justifier votre réponse.
Calculer la matrice inverse $A^{-1}$ en utilisant la méthode du pivot de Gauss. Détaillez les étapes du pivot de Gauss.
Utiliser la matrice inverse $A^{-1}$ pour résoudre le système d'équations $AX = B$. Donner les valeurs de $x$, $y$ et $z$.
Vérifier votre solution en remplaçant les valeurs de $x$, $y$ et $z$ trouvées dans le système d'équations initial.

Correction :

Forme matricielle $AX = B$ :

Le système d'équations peut s'écrire sous forme matricielle comme suit : $$ \begin{pmatrix} 1 & 2 & -1 \\ 2 & -1 & 3 \\ -1 & 3 & 2 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ -5 \\ 7 \end{pmatrix} $$ Ici, nous avons : $$ A = \begin{pmatrix} 1 & 2 & -1 \\ 2 & -1 & 3 \\ -1 & 3 & 2 \end{pmatrix}, \quad X = \begin{pmatrix} x \\ y \\ z \end{pmatrix}, \quad B = \begin{pmatrix} 2 \\ -5 \\ 7 \end{pmatrix} $$
Déterminant de $A$ et inversibilité :

Calculons le déterminant de la matrice $A$ en utilisant la règle de Sarrus ou le développement par rapport à une ligne ou une colonne. Développons par rapport à la première ligne : $$ \det(A) = 1 \cdot \begin{vmatrix} -1 & 3 \\ 3 & 2 \end{vmatrix} - 2 \cdot \begin{vmatrix} 2 & 3 \\ -1 & 2 \end{vmatrix} + (-1) \cdot \begin{vmatrix} 2 & -1 \\ -1 & 3 \end{vmatrix} $$ $$ = 1 \cdot ((-1) \times 2 - 3 \times 3) - 2 \cdot ((2 \times 2) - (3 \times -1)) - 1 \cdot ((2 \times 3) - (-1 \times -1)) $$ $$ = 1 \cdot (-2 - 9) - 2 \cdot (4 + 3) - 1 \cdot (6 - 1) $$ $$ = 1 \cdot (-11) - 2 \cdot (7) - 1 \cdot (5) = -11 - 14 - 5 = -30 $$

Puisque $\det(A) = -30 \neq 0$, la matrice $A$ est inversible.
Calcul de la matrice inverse $A^{-1}$ par Pivot de Gauss :

On forme la matrice augmentée $[A | I_3]$ et on applique le pivot de Gauss : $$ \left[ \begin{array}{ccc|ccc} 1 & 2 & -1 & 1 & 0 & 0 \\ 2 & -1 & 3 & 0 & 1 & 0 \\ -1 & 3 & 2 & 0 & 0 & 1 \end{array} \right] \xrightarrow{L_2 \leftarrow L_2 - 2L_1, L_3 \leftarrow L_3 + L_1} \left[ \begin{array}{ccc|ccc} 1 & 2 & -1 & 1 & 0 & 0 \\ 0 & -5 & 5 & -2 & 1 & 0 \\ 0 & 5 & 1 & 1 & 0 & 1 \end{array} \right] $$ $$ \xrightarrow{L_2 \leftarrow -\frac{1}{5}L_2} \left[ \begin{array}{ccc|ccc} 1 & 2 & -1 & 1 & 0 & 0 \\ 0 & 1 & -1 & \frac{2}{5} & -\frac{1}{5} & 0 \\ 0 & 5 & 1 & 1 & 0 & 1 \end{array} \right] \xrightarrow{L_3 \leftarrow L_3 - 5L_2} \left[ \begin{array}{ccc|ccc} 1 & 2 & -1 & 1 & 0 & 0 \\ 0 & 1 & -1 & \frac{2}{5} & -\frac{1}{5} & 0 \\ 0 & 0 & 6 & -1 & 1 & 1 \end{array} \right] $$ $$ \xrightarrow{L_3 \leftarrow \frac{1}{6}L_3} \left[ \begin{array}{ccc|ccc} 1 & 2 & -1 & 1 & 0 & 0 \\ 0 & 1 & -1 & \frac{2}{5} & -\frac{1}{5} & 0 \\ 0 & 0 & 1 & -\frac{1}{6} & \frac{1}{6} & \frac{1}{6} \end{array} \right] \xrightarrow{L_1 \leftarrow L_1 + L_3, L_2 \leftarrow L_2 + L_3} \left[ \begin{array}{ccc|ccc} 1 & 2 & 0 & \frac{5}{6} & \frac{1}{6} & \frac{1}{6} \\ 0 & 1 & 0 & \frac{7}{30} & -\frac{1}{30} & \frac{1}{6} \\ 0 & 0 & 1 & -\frac{1}{6} & \frac{1}{6} & \frac{1}{6} \end{array} \right] $$ $$ \xrightarrow{L_1 \leftarrow L_1 - 2L_2} \left[ \begin{array}{ccc|ccc} 1 & 0 & 0 & \frac{5}{6} - 2 \cdot \frac{7}{30} & \frac{1}{6} - 2 \cdot (-\frac{1}{30}) & \frac{1}{6} - 2 \cdot \frac{1}{6} \\ 0 & 1 & 0 & \frac{7}{30} & -\frac{1}{30} & \frac{1}{6} \\ 0 & 0 & 1 & -\frac{1}{6} & \frac{1}{6} & \frac{1}{6} \end{array} \right] = \left[ \begin{array}{ccc|ccc} 1 & 0 & 0 & \frac{25-14}{30} & \frac{5+2}{30} & -\frac{1}{6} \\ 0 & 1 & 0 & \frac{7}{30} & -\frac{1}{30} & \frac{1}{6} \\ 0 & 0 & 1 & -\frac{1}{6} & \frac{1}{6} & \frac{1}{6} \end{array} \right] $$ $$ = \left[ \begin{array}{ccc|ccc} 1 & 0 & 0 & \frac{11}{30} & \frac{7}{30} & -\frac{5}{30} \\ 0 & 1 & 0 & \frac{7}{30} & -\frac{1}{30} & \frac{5}{30} \\ 0 & 0 & 1 & -\frac{5}{30} & \frac{5}{30} & \frac{5}{30} \end{array} \right] = \left[ \begin{array}{ccc|ccc} 1 & 0 & 0 & \frac{11}{30} & \frac{7}{30} & -\frac{1}{6} \\ 0 & 1 & 0 & \frac{7}{30} & -\frac{1}{30} & \frac{1}{6} \\ 0 & 0 & 1 & -\frac{1}{6} & \frac{1}{6} & \frac{1}{6} \end{array} \right] $$ Donc, $A^{-1} = \begin{pmatrix} \frac{11}{30} & \frac{7}{30} & -\frac{1}{6} \\ \frac{7}{30} & -\frac{1}{30} & \frac{1}{6} \\ -\frac{1}{6} & \frac{1}{6} & \frac{1}{6} \end{pmatrix} = \frac{1}{30} \begin{pmatrix} 11 & 7 & -5 \\ 7 & -1 & 5 \\ -5 & 5 & 5 \end{pmatrix}$.
Résolution du système $AX = B$ avec $A^{-1}$ :

La solution est donnée par $X = A^{-1}B$. Calculons $A^{-1}B$ : $$ X = A^{-1}B = \frac{1}{30} \begin{pmatrix} 11 & 7 & -5 \\ 7 & -1 & 5 \\ -5 & 5 & 5 \end{pmatrix} \begin{pmatrix} 2 \\ -5 \\ 7 \end{pmatrix} = \frac{1}{30} \begin{pmatrix} (11 \times 2) + (7 \times -5) + (-5 \times 7) \\ (7 \times 2) + (-1 \times -5) + (5 \times 7) \\ (-5 \times 2) + (5 \times -5) + (5 \times 7) \end{pmatrix} $$ $$ = \frac{1}{30} \begin{pmatrix} 22 - 35 - 35 \\ 14 + 5 + 35 \\ -10 - 25 + 35 \end{pmatrix} = \frac{1}{30} \begin{pmatrix} -48 \\ 54 \\ 0 \end{pmatrix} = \begin{pmatrix} -\frac{48}{30} \\ \frac{54}{30} \\ \frac{0}{30} \end{pmatrix} = \begin{pmatrix} -\frac{8}{5} \\ \frac{9}{5} \\ 0 \end{pmatrix} $$

Ainsi, $X = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -\frac{8}{5} \\ \frac{9}{5} \\ 0 \end{pmatrix}$, ce qui signifie $x = -\frac{8}{5}$, $y = \frac{9}{5}$ et $z = 0$.
Vérification de la solution :

Substituons $x = -\frac{8}{5}$, $y = \frac{9}{5}$ et $z = 0$ dans le système d'équations initial : $$ \begin{cases} x + 2y - z = -\frac{8}{5} + 2 \left(\frac{9}{5}\right) - 0 = -\frac{8}{5} + \frac{18}{5} = \frac{10}{5} = 2 \\ 2x - y + 3z = 2 \left(-\frac{8}{5}\right) - \frac{9}{5} + 3(0) = -\frac{16}{5} - \frac{9}{5} = -\frac{25}{5} = -5 \\ -x + 3y + 2z = - \left(-\frac{8}{5}\right) + 3 \left(\frac{9}{5}\right) + 2(0) = \frac{8}{5} + \frac{27}{5} = \frac{35}{5} = 7 \end{cases} $$ Les trois équations sont bien vérifiées. La solution $x = -\frac{8}{5}$, $y = \frac{9}{5}$ et $z = 0$ est donc correcte.

Exercice 8 - Inverser une Matrice à Partir d'une Égalité

Soit $ A=\left( \begin{array}{ccc} -1&1&1\\ 1&-1&1\\ 1&1&-1 \end{array}\right)$. Montrer que $A^2=2I_3-A$. En déduire que $A$ est inversible et exprimer $A^{-1}$ en fonction de $A$ et $I_3$.
Soit $ A=\begin{pmatrix} 1 & 0 & 2 \cr 0 & -1 & 1 \cr 1 & -2 & 0 \cr \end{pmatrix} .$ Calculer $ A^3-5A .$ Expliquer pourquoi, à partir de ce calcul, on ne peut pas déduire directement que $A$ est inversible et exprimer $ A^{-1} $ en fonction de $A^2$, $A$ et $I_3$ comme dans les questions précédentes.**
Soit $A=\begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix}$. Calculer $A^2-3A+3I_3$. En déduire que $A$ est inversible, et exprimer $A^{-1}$ en fonction de $A$ et $I_3$.

Correction :

Vérification de $A^2=2I_3-A$ :

Calculons $A^2$ pour $A=\left( \begin{array}{ccc} -1&1&1\\ 1&-1&1\\ 1&1&-1 \end{array}\right)$: $$ A^2 = \left( \begin{array}{ccc} -1&1&1\\ 1&-1&1\\ 1&1&-1 \end{array}\right) \left( \begin{array}{ccc} -1&1&1\\ 1&-1&1\\ 1&1&-1 \end{array}\right) $$ $$ A^2 = \left( \begin{array}{ccc} (1+1+1)&(-1-1+1)&(-1+1-1)\\ (-1-1+1)&(1+1+1)&(1-1-1)\\ (-1+1-1)&(1-1-1)&(1+1+1) \end{array}\right) = \left( \begin{array}{ccc} 3&-1&-1\\ -1&3&-1\\ -1&-1&3 \end{array}\right) $$

Calculons $2I_3 - A$ : $$ 2I_3 - A = 2\left( \begin{array}{ccc} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}\right) - \left( \begin{array}{ccc} -1&1&1\\ 1&-1&1\\ 1&1&-1 \end{array}\right) = \left( \begin{array}{ccc} 2&0&0\\ 0&2&0\\ 0&0&2 \end{array}\right) - \left( \begin{array}{ccc} -1&1&1\\ 1&-1&1\\ 1&1&-1 \end{array}\right) = \left( \begin{array}{ccc} 3&-1&-1\\ -1&3&-1\\ -1&-1&3 \end{array}\right) $$

On constate que $A^2 = 2I_3 - A$. L'égalité est donc vérifiée.

Déduction de l'inversibilité de $A$ et de $A^{-1}$ :

L'égalité $A^2 = 2I_3 - A$ peut se réécrire : $$ A^2 + A = 2I_3 $$ Factorisons $A$ à gauche dans le membre de gauche : $$ A(A + I_3) = 2I_3 $$ Pour faire apparaître $I_3$ à droite, on peut diviser par 2 (ou multiplier par $1/2$) : $$ A \left( \frac{1}{2}(A + I_3) \right) = I_3 $$ Cette égalité est de la forme $A \cdot B = I_3$, avec $B = \frac{1}{2}(A + I_3)$. Par définition, cela signifie que $B$ est l'inverse à droite de $A$. De même, on peut factoriser $A$ à droite dans $A^2 + A = 2I_3$ : $$ (A + I_3)A = 2I_3 \Rightarrow \left( \frac{1}{2}(A + I_3) \right) A = I_3 $$ Donc, $B = \frac{1}{2}(A + I_3)$ est aussi l'inverse à gauche de $A$. Par conséquent, $A$ est inversible et son inverse est $A^{-1} = \frac{1}{2}(A + I_3)$.

Expression de $A^{-1}$ en fonction de $A$ et $I_3$ :

Nous avons trouvé : $A^{-1} = \frac{1}{2}(A + I_3)$. On peut aussi écrire : $A^{-1} = \frac{1}{2}A + \frac{1}{2}I_3$.
Calcul de $A^3-5A$ pour $ A=\begin{pmatrix} 1 & 0 & 2 \cr 0 & -1 & 1 \cr 1 & -2 & 0 \cr \end{pmatrix} $ :

Calculons d'abord $A^2$: $$ A^2 = \begin{pmatrix} 1 & 0 & 2 \cr 0 & -1 & 1 \cr 1 & -2 & 0 \cr \end{pmatrix} \begin{pmatrix} 1 & 0 & 2 \cr 0 & -1 & 1 \cr 1 & -2 & 0 \cr \end{pmatrix} = \begin{pmatrix} (1+0+2)&(0+0-4)&(2+0+0) \cr (0+0+1)&(0+1-2)&(0-1+0) \cr (1+0+0)&(0+2+0)&(2-2+0) \cr \end{pmatrix} = \begin{pmatrix} 3 & -4 & 2 \cr 1 & -1 & -1 \cr 1 & 2 & 0 \cr \end{pmatrix} $$

Calculons ensuite $A^3 = A^2 \cdot A$: $$ A^3 = A^2 A = \begin{pmatrix} 3 & -4 & 2 \cr 1 & -1 & -1 \cr 1 & 2 & 0 \cr \end{pmatrix} \begin{pmatrix} 1 & 0 & 2 \cr 0 & -1 & 1 \cr 1 & -2 & 0 \cr \end{pmatrix} = \begin{pmatrix} (3+0+2)&(0+4-4)&(6-4+0) \cr (1+0-1)&(0+1+2)&(2-1+0) \cr (1+0+0)&(0-2+0)&(2+2+0) \cr \end{pmatrix} = \begin{pmatrix} 5 & 0 & 2 \cr 0 & 3 & 1 \cr 1 & -2 & 4 \cr \end{pmatrix} $$

Enfin, calculons $A^3 - 5A$ : $$ A^3 - 5A = \begin{pmatrix} 5 & 0 & 2 \cr 0 & 3 & 1 \cr 1 & -2 & 4 \cr \end{pmatrix} - 5 \begin{pmatrix} 1 & 0 & 2 \cr 0 & -1 & 1 \cr 1 & -2 & 0 \cr \end{pmatrix} = \begin{pmatrix} 5-5 & 0-0 & 2-10 \cr 0-0 & 3-(-5) & 1-5 \cr 1-5 & -2-(-10) & 4-0 \cr \end{pmatrix} = \begin{pmatrix} 0 & 0 & -8 \cr 0 & 8 & -4 \cr -4 & 8 & 4 \cr \end{pmatrix} $$

Explication : Le calcul donne $A^3-5A = \begin{pmatrix} 0 & 0 & -8 \cr 0 & 8 & -4 \cr -4 & 8 & 4 \cr \end{pmatrix}$. Cette matrice n'est pas un multiple de la matrice identité $I_3$. Par conséquent, il n'existe pas de scalaire $c$ tel que $A^3-5A = cI_3$. La méthode utilisée dans les questions 1 et 3 pour déduire l'inversibilité et l'inverse de $A$ repose sur l'obtention d'une égalité de la forme $P(A) = cI_3$ où $P(A)$ est une expression polynomiale en $A$ et $c$ est un scalaire non nul. Ici, nous n'obtenons pas une telle forme, donc nous ne pouvons pas directement appliquer cette méthode pour trouver $A^{-1}$ à partir du calcul de $A^3-5A$.

Pour déterminer si $A$ est inversible et trouver son inverse, il faudrait utiliser d'autres méthodes, comme le calcul du déterminant de $A$ ou la méthode du pivot de Gauss.
Calcul de $A^2-3A+3I_3$ pour $A=\begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix}$ :

Calculons $A^2$: $$ A^2 = \begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix} \begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix}$$ $$ A^2 = \begin{pmatrix} (0-1-1)&(0+2+1)&(0-1-2)\\ (0-2-1)&(-1+4+1)&(1-2-2)\\ (0+1+2)&(1-2-2)&(-1+1+4) \end{pmatrix} = \begin{pmatrix} -2&3&-3\\ -3&4&-3\\ 3&-3&4 \end{pmatrix} $$

Maintenant, calculons $A^2-3A+3I_3$: $$ A^2-3A+3I_3 = \begin{pmatrix} -2&3&-3\\ -3&4&-3\\ 3&-3&4 \end{pmatrix} - 3\begin{pmatrix} 0&1&-1\\ -1&2&-1\\ 1&-1&2 \end{pmatrix} + 3\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix} $$ $$ = \begin{pmatrix} -2-0+3 & 3-3+0 & -3+3+0 \\ -3+3+0 & 4-6+3 & -3+3+0 \\ 3-3+0 & -3+3+0 & 4-6+3 \end{pmatrix} = \begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{pmatrix} = I_3 $$

Déduction de l'inversibilité de $A$ et de $A^{-1}$ :

L'égalité $A^2-3A+3I_3 = I_3$ peut se réécrire : $$ A^2-3A+3I_3 = I_3 \Rightarrow A^2-3A = -2I_3 \Rightarrow 3I_3 - A^2 = -A \Rightarrow A = 3I_3 - A^2 $$ Ou, en partant de $A^2-3A+3I_3 = I_3$, on peut isoler $I_3$ : $$ I_3 = A^2-3A+3I_3 \Rightarrow I_3 - 3I_3 = A^2-3A \Rightarrow -2I_3 = A^2-3A \Rightarrow 2I_3 = 3A - A^2 $$ $$ I_3 = A(3I_3 - A) = (3I_3 - A)A $$ En divisant par 2 : $$ I_3 = A \left( \frac{1}{2}(3I_3 - A) \right) = \left( \frac{1}{2}(3I_3 - A) \right) A $$

Déduction de l'inversibilité de $A$ et de $A^{-1}$ :

L'égalité $I_3 = A \left( \frac{1}{2}(3I_3 - A) \right) = \left( \frac{1}{2}(3I_3 - A) \right) A$ montre que $A$ est inversible et que son inverse est $A^{-1} = \frac{1}{2}(3I_3 - A)$.

Expression de $A^{-1}$ en fonction de $A$ et $I_3$ :

Nous avons trouvé : $A^{-1} = \frac{1}{2}(3I_3 - A) = \frac{3}{2}I_3 - \frac{1}{2}A$.

Exercice 9 - Calcul d'Inverse par Pivot de Gauss

Déterminer si les matrices suivantes sont inversibles et, si oui, calculer leur inverse en utilisant la méthode du pivot de Gauss. $$A=\left( \begin{array}{rcl} 1&1&2\\ 1&2&1\\ 2&1&1 \end{array} \right),\quad B=\left( \begin{array}{rcl} 0&1&2\\ 1&1&2\\ 0&2&3 \end{array} \right),\quad C=\left( \begin{array}{rcl} 1&4&7\\ 2&5&8\\ 3&6&9 \end{array} \right),\quad I=\left( \begin{array}{rcl} i&-1&2i\\ 2&0&2\\ -1&0&1 \end{array} \right). \text{ (matrice à coefficients dans $\mathbb{C}$)}$$

Correction :

Matrice $A=\left( \begin{array}{rcl} 1&1&2\\ 1&2&1\\ 2&1&1 \end{array} \right)$ :

Appliquons la méthode du pivot de Gauss pour inverser $A$. On forme la matrice augmentée $[A | I_3]$ : $$ \left[ \begin{array}{ccc|ccc} 1&1&2 & 1&0&0\\ 1&2&1 & 0&1&0\\ 2&1&1 & 0&0&1 \end{array} \right] $$

Étape 1: Transformations pour obtenir des zéros sous le premier pivot (en position (1,1)).
$L_2 \leftarrow L_2 - L_1$ $L_3 \leftarrow L_3 - 2L_1$
$$ \left[ \begin{array}{ccc|ccc} 1&1&2 & 1&0&0\\ 0&1&-1 & -1&1&0\\ 0&-1&-3 & -2&0&1 \end{array} \right] $$

Étape 2: Transformations pour obtenir un zéro sous le deuxième pivot (en position (2,2)).
$L_3 \leftarrow L_3 + L_2$
$$ \left[ \begin{array}{ccc|ccc} 1&1&2 & 1&0&0\\ 0&1&-1 & -1&1&0\\ 0&0&-4 & -3&1&1 \end{array} \right] $$

Étape 3: Normalisation du troisième pivot (en position (3,3)) pour obtenir 1.
$L_3 \leftarrow -\frac{1}{4}L_3$
$$ \left[ \begin{array}{ccc|ccc} 1&1&2 & 1&0&0\\ 0&1&-1 & -1&1&0\\ 0&0&1 & 3/4&-1/4&-1/4 \end{array} \right] $$

Étape 4: Transformations pour obtenir des zéros au-dessus du troisième pivot.
$L_1 \leftarrow L_1 - 2L_3$ $L_2 \leftarrow L_2 + L_3$
$$ \left[ \begin{array}{ccc|ccc} 1&1&0 & -1/2&1/2&1/2\\ 0&1&0 & -1/4&3/4&-1/4\\ 0&0&1 & 3/4&-1/4&-1/4 \end{array} \right] $$

Étape 5: Transformation pour obtenir un zéro au-dessus du deuxième pivot.
$L_1 \leftarrow L_1 - L_2$
$$ \left[ \begin{array}{ccc|ccc} 1&0&0 & -1/4 & -1/4 & 3/4\\ 0&1&0 & -1/4&3/4&-1/4\\ 0&0&1 & 3/4&-1/4&-1/4 \end{array} \right] $$

Donc, $A^{-1} = \left( \begin{array}{rcl} -1/4&-1/4&3/4\\ -1/4&3/4&-1/4\\ 3/4&-1/4&-1/4 \end{array} \right) = \frac{1}{4} \left( \begin{array}{rcl} -1&-1&3\\ -1&3&-1\\ 3&-1&-1 \end{array} \right)$.

Conclusion pour $A$ : La matrice $A$ est inversible et $A^{-1} = \frac{1}{4} \left( \begin{array}{rcl} -1&-1&3\\ -1&3&-1\\ 3&-1&-1 \end{array} \right)$.

Matrice $B=\left( \begin{array}{rcl} 0&1&2\\ 1&1&2\\ 0&2&3 \end{array} \right)$ :

Matrice augmentée $[B | I_3]$ : $$ \left[ \begin{array}{ccc|ccc} 0&1&2 & 1&0&0\\ 1&1&2 & 0&1&0\\ 0&2&3 & 0&0&1 \end{array} \right] $$

Étape 1: Échange de lignes pour avoir un pivot non nul en position (1,1).
$L_1 \leftrightarrow L_2$
$$ \left[ \begin{array}{ccc|ccc} 1&1&2 & 0&1&0\\ 0&1&2 & 1&0&0\\ 0&2&3 & 0&0&1 \end{array} \right] $$

Étape 2: Transformation pour obtenir un zéro sous le deuxième pivot (en position (2,2)).
$L_3 \leftarrow L_3 - 2L_2$
$$ \left[ \begin{array}{ccc|ccc} 1&1&2 & 0&1&0\\ 0&1&2 & 1&0&0\\ 0&0&-1 & -2&0&1 \end{array} \right] $$

Étape 3: Normalisation du troisième pivot (en position (3,3)).
$L_3 \leftarrow -L_3$
$$ \left[ \begin{array}{ccc|ccc} 1&1&2 & 0&1&0\\ 0&1&2 & 1&0&0\\ 0&0&1 & 2&0&-1 \end{array} \right] $$

Étape 4: Transformations pour obtenir des zéros au-dessus du troisième pivot.
$L_1 \leftarrow L_1 - 2L_3$ $L_2 \leftarrow L_2 - 2L_3$
$$ \left[ \begin{array}{ccc|ccc} 1&1&0 & -4&1&2\\ 0&1&0 & -3&0&2\\ 0&0&1 & 2&0&-1 \end{array} \right] $$

Étape 5: Transformation pour obtenir un zéro au-dessus du deuxième pivot.
$L_1 \leftarrow L_1 - L_2$
$$ \left[ \begin{array}{ccc|ccc} 1&0&0 & -1 & 1 & 0\\ 0&1&0 & -3&0&2\\ 0&0&1 & 2&0&-1 \end{array} \right] $$

Donc, $B^{-1}=\left( \begin{array}{rcl} -1&1&0\\ -3&0&2\\ 2&0&-1 \end{array} \right)$.

Conclusion pour $B$ : La matrice $B$ est inversible et $B^{-1}=\left( \begin{array}{rcl} -1&1&0\\ -3&0&2\\ 2&0&-1 \end{array} \right)$.

Matrice $C=\left( \begin{array}{rcl} 1&4&7\\ 2&5&8\\ 3&6&9 \end{array} \right)$ :

Matrice augmentée $[C | I_3]$ : $$ \left[ \begin{array}{ccc|ccc} 1&4&7 & 1&0&0\\ 2&5&8 & 0&1&0\\ 3&6&9 & 0&0&1 \end{array} \right] $$

Étape 1: Transformations pour obtenir des zéros sous le premier pivot.
$L_2 \leftarrow L_2 - 2L_1$ $L_3 \leftarrow L_3 - 3L_1$
$$ \left[ \begin{array}{ccc|ccc} 1&4&7 & 1&0&0\\ 0&-3&-6 & -2&1&0\\ 0&-6&-12 & -3&0&1 \end{array} \right] $$

Étape 2: Transformation pour obtenir un zéro sous le deuxième pivot.
$L_3 \leftarrow L_3 - 2L_2$
$$ \left[ \begin{array}{ccc|ccc} 1&4&7 & 1&0&0\\ 0&-3&-6 & -2&1&0\\ 0&0&0 & 1&-2&1 \end{array} \right] $$

On obtient une ligne de zéros dans la partie gauche. Cela signifie que la matrice $C$ n'est pas inversible.

Conclusion pour $C$ : La matrice $C$ n'est pas inversible.

Matrice $I=\left( \begin{array}{rcl} i&-1&2i\\ 2&0&2\\ -1&0&1 \end{array} \right)$ (matrice à coefficients complexes) :

Matrice augmentée $[I | I_3]$ : $$ \left[ \begin{array}{ccc|ccc} i&-1&2i & 1&0&0\\ 2&0&2 & 0&1&0\\ -1&0&1 & 0&0&1 \end{array} \right] $$

Étape 1: Échange de lignes pour éviter de diviser par $i$ directement et avoir un pivot réel si possible.
$L_1 \leftrightarrow L_3$
$$ \left[ \begin{array}{ccc|ccc} -1&0&1 & 0&0&1 \\ 2&0&2 & 0&1&0 \\ i&-1&2i & 1&0&0 \end{array} \right] $$

Étape 2: Normalisation du premier pivot.
$L_1 \leftarrow -L_1$
$$ \left[ \begin{array}{ccc|ccc} 1&0&-1 & 0&0&-1 \\ 2&0&2 & 0&1&0 \\ i&-1&2i & 1&0&0 \end{array} \right] $$

Étape 3: Transformations pour obtenir des zéros sous le premier pivot.
$L_2 \leftarrow L_2 - 2L_1$ $L_3 \leftarrow L_3 - iL_1$
$$ \left[ \begin{array}{ccc|ccc} 1&0&-1 & 0&0&-1 \\ 0&0&4 & 0&1&2 \\ 0&-1&3i & 1&0&i \end{array} \right] $$

Étape 4: Échange de lignes pour avoir un pivot non nul en position (2,2).
$L_2 \leftrightarrow L_3$
$$ \left[ \begin{array}{ccc|ccc} 1&0&-1 & 0&0&-1 \\ 0&-1&3i & 1&0&i \\ 0&0&4 & 0&1&2 \end{array} \right] $$

Étape 5: Normalisation du deuxième pivot.
$L_2 \leftarrow -L_2$
$$ \left[ \begin{array}{ccc|ccc} 1&0&-1 & 0&0&-1 \\ 0&1&-3i & -1&0&-i \\ 0&0&4 & 0&1&2 \end{array} \right] $$

Étape 6: Normalisation du troisième pivot.
$L_3 \leftarrow \frac{1}{4}L_3$
$$ \left[ \begin{array}{ccc|ccc} 1&0&-1 & 0&0&-1 \\ 0&1&-3i & -1&0&-i \\ 0&0&1 & 0&1/4&1/2 \end{array} \right] $$

Étape 7: Transformations pour obtenir des zéros au-dessus du troisième pivot.
$L_1 \leftarrow L_1 + L_3$ $L_2 \leftarrow L_2 + 3iL_3$
$$ \left[ \begin{array}{ccc|ccc} 1&0&0 & 0&1/4&-1/2 \\ 0&1&0 & -1&3i/4&i/2 \\ 0&0&1 & 0&1/4&1/2 \end{array} \right] $$

Donc, $I^{-1} = \left( \begin{array}{rcl} 0&1/4&-1/2\\ -1&3i/4&i/2\\ 0&1/4&1/2 \end{array} \right)$.

Conclusion pour $I$ : La matrice $I$ est inversible et $I^{-1} = \left( \begin{array}{rcl} 0&1/4&-1/2\\ -1&3i/4&i/2\\ 0&1/4&1/2 \end{array} \right)$.

Exercice 10 - Inversibilité de $I_n - A$ pour Matrice Nilpotente $A$

Soit $A\in\mathcal M_n(\mathbb R)$ une matrice nilpotente, c'est-à-dire qu'il existe un entier $p\geq 1$ tel que $A^p=0$. Démontrer que la matrice $I_n-A$ est inversible, et déterminer une expression pour son inverse en fonction de $A$ et de puissances de $A$.

Correction :

Définition de matrice nilpotente : Une matrice $A$ est nilpotente s'il existe un entier $p \geq 1$ tel que $A^p = 0$, où $0$ est la matrice nulle. L'entier $p$ est appelé indice de nilpotence (on peut prendre le plus petit tel entier comme indice).

Objectif : Montrer que la matrice $I_n - A$ est inversible et trouver une expression pour son inverse en fonction de $A$ et de ses puissances.

Idée : Rappelons la formule de la somme géométrique pour les nombres réels : pour $x \neq 1$, $1 + x + x^2 + \dots + x^{p-1} = \frac{1-x^p}{1-x}$. Si $|x| < 1$, alors $x^p \rightarrow 0$ quand $p \rightarrow \infty$, et on a ce que l'on appelle une série géométrique $1 + x + x^2 + \dots = \frac{1}{1-x} = (1-x)^{-1}$. Nous allons essayer d'adapter cette idée aux matrices.

Puisque $A$ est nilpotente, il existe un entier $p \geq 1$ tel que $A^p = 0$. Considérons la matrice $B$ définie comme la somme finie des puissances de $A$ de $A^0=I_n$ à $A^{p-1}$: $$ B = I_n+A+A^2+\dots+A^{p-1} = \sum_{k=0}^{p-1} A^k $$

Calculons le produit $(I_n-A)B$ : $$ (I_n-A)B = (I_n-A)(I_n+A+A^2+\dots+A^{p-1}) $$ Développons ce produit : $$ = I_n(I_n+A+A^2+\dots+A^{p-1}) - A(I_n+A+A^2+\dots+A^{p-1}) $$ $$ = (I_n+A+A^2+\dots+A^{p-1}) - (A+A^2+A^3+\dots+A^p) $$

Observons que beaucoup de termes se simplifient (télescopage). Tous les termes à partir de $A$ jusqu'à $A^{p-1}$ se cancellent : $$ = I_n + (A-A) + (A^2-A^2) + \dots + (A^{p-1}-A^{p-1}) - A^p = I_n - A^p $$

Puisque $A^p = 0$ par hypothèse (nilpotence de $A$), on a : $$ (I_n-A)B = I_n - 0 = I_n $$

De même, calculons le produit $B(I_n-A)$ : $$ B(I_n-A) = (I_n+A+A^2+\dots+A^{p-1})(I_n-A) $$ $$ = I_n(I_n-A) + A(I_n-A) + A^2(I_n-A) + \dots + A^{p-1}(I_n-A) $$ $$ = (I_n-A) + (A-A^2) + (A^2-A^3) + \dots + (A^{p-1}-A^p) $$

Encore une fois, on a un télescopage : $$ = I_n - A + A - A^2 + A^2 - A^3 + \dots + A^{p-1} - A^p = I_n - A^p = I_n - 0 = I_n $$

Nous avons donc montré que $(I_n-A)B = B(I_n-A) = I_n$. Par définition, cela signifie que la matrice $I_n-A$ est inversible et que son inverse est $B$.

Conclusion : La matrice $I_n-A$ est inversible, et son inverse est donnée par : $$ (I_n-A)^{-1} = B = I_n+A+A^2+\dots+A^{p-1} = \sum_{k=0}^{p-1} A^k $$ où $p$ est un entier tel que $A^p = 0$. (En fait, cette formule est valable pour tout indice de nilpotence $p$, et même pour le plus petit indice de nilpotence).

Exercice 11 - Matrices Stochastiques et Stabilité par Produit

Pour $n\geq 1$, on note $\mathcal D$ l'ensemble des matrices $A$ de $\mathcal M_n(\mathbb R)$ telles que $a_{i,j}\geq 0$ pour tout $i,j$ et $\sum_{j=1}^n a_{i,j}=1$ pour tout $i=1,\dots,n$.

Démontrer que $\mathcal D$ est stable par produit.
Déterminer les matrices $A$ de $\mathcal D$ qui sont inversibles et telles que $A^{-1}\in\mathcal D$.

Correction :

Stabilité de $\mathcal D$ par produit :

Soient $A$ et $B$ deux matrices appartenant à $\mathcal D$. Nous devons montrer que leur produit $C = AB$ appartient aussi à $\mathcal D$. Pour cela, nous devons vérifier deux conditions pour $C = (c_{ij})$ :
1. Tous les coefficients de $C$ sont non négatifs : $c_{ij} \geq 0$ pour tous $i, j$.
2. La somme des coefficients de chaque ligne de $C$ est égale à 1 : $\sum_{j=1}^n c_{ij} = 1$ pour tout $i = 1, \dots, n$.
Condition (a) : Non-négativité des coefficients de $C$ :

Le coefficient $(i, j)$ de la matrice produit $C = AB$ est donné par la formule : $$ c_{ij} = \sum_{k=1}^n a_{ik} b_{kj} $$ Puisque $A \in \mathcal D$ et $B \in \mathcal D$, par définition de $\mathcal D$, tous les coefficients de $A$ et $B$ sont non négatifs : $a_{ik} \geq 0$ et $b_{kj} \geq 0$ pour tous $i, k, j$. Un produit de nombres non négatifs est non négatif, et une somme de nombres non négatifs est non négative. Donc, chaque terme $a_{ik} b_{kj} \geq 0$, et leur somme $c_{ij} = \sum_{k=1}^n a_{ik} b_{kj} \geq 0$. La condition (a) est donc vérifiée.

Condition (b) : Somme des coefficients de chaque ligne de $C$ égale à 1 :

Calculons la somme des coefficients de la ligne $i$ de $C$ : $$ \sum_{j=1}^n c_{ij} = \sum_{j=1}^n \left( \sum_{k=1}^n a_{ik} b_{kj} \right) $$ On peut intervertir l'ordre des sommes (somme finie) : $$ = \sum_{k=1}^n \sum_{j=1}^n a_{ik} b_{kj} = \sum_{k=1}^n a_{ik} \left( \sum_{j=1}^n b_{kj} \right) $$

Puisque $B \in \mathcal D$, la somme des coefficients de chaque ligne de $B$ est égale à 1. En particulier, pour la ligne $k$ de $B$, $\sum_{j=1}^n b_{kj} = 1$. Donc, on remplace $\sum_{j=1}^n b_{kj}$ par 1 dans l'expression ci-dessus : $$ \sum_{j=1}^n c_{ij} = \sum_{k=1}^n a_{ik} \cdot 1 = \sum_{k=1}^n a_{ik} $$

Puisque $A \in \mathcal D$, la somme des coefficients de chaque ligne de $A$ est égale à 1. En particulier, pour la ligne $i$ de $A$, $\sum_{k=1}^n a_{ik} = 1$. Donc, $$ \sum_{j=1}^n c_{ij} = \sum_{k=1}^n a_{ik} = 1 $$ La condition (b) est donc vérifiée.

Conclusion pour la question 1 : Puisque les conditions (a) et (b) sont vérifiées pour la matrice produit $C = AB$, on a $C = AB \in \mathcal D$. Donc, $\mathcal D$ est stable par produit.
Matrices $A \in \mathcal D$ inversibles telles que $A^{-1} \in \mathcal D$ :

On cherche les matrices stochastiques (dans $\mathcal D$) qui sont inversibles et dont l'inverse est aussi stochastique (dans $\mathcal D$).

Un exemple important de telles matrices sont les matrices de permutation.

Matrices de permutation : Une matrice de permutation est une matrice carrée dont chaque ligne et chaque colonne contient exactement un coefficient égal à 1, et tous les autres coefficients sont égaux à 0.

Propriétés des matrices de permutation :
1. Une matrice de permutation est stochastique (car la somme des coefficients de chaque ligne est 1, et les coefficients sont $\geq 0$). Donc, les matrices de permutation sont dans $\mathcal D$.
2. Une matrice de permutation est inversible.
3. L'inverse d'une matrice de permutation est aussi une matrice de permutation (c'est sa transposée). Donc, l'inverse d'une matrice de permutation est aussi stochastique (dans $\mathcal D$).
Conclusion pour la question 2 : Les matrices de permutation sont des exemples de matrices $A \in \mathcal D$ qui sont inversibles et telles que $A^{-1} \in \mathcal D$. En fait, on peut montrer que les matrices de permutation sont les seules matrices dans $\mathcal D$ qui ont un inverse aussi dans $\mathcal D$. La démonstration de cette unicité est plus avancée.

Exercice 12 - Matrices de Rotation 2D

Démontrer que la forme générale d'une matrice de rotation 2D d'angle $\theta$ est donnée par : $$ R(\theta) = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} $$
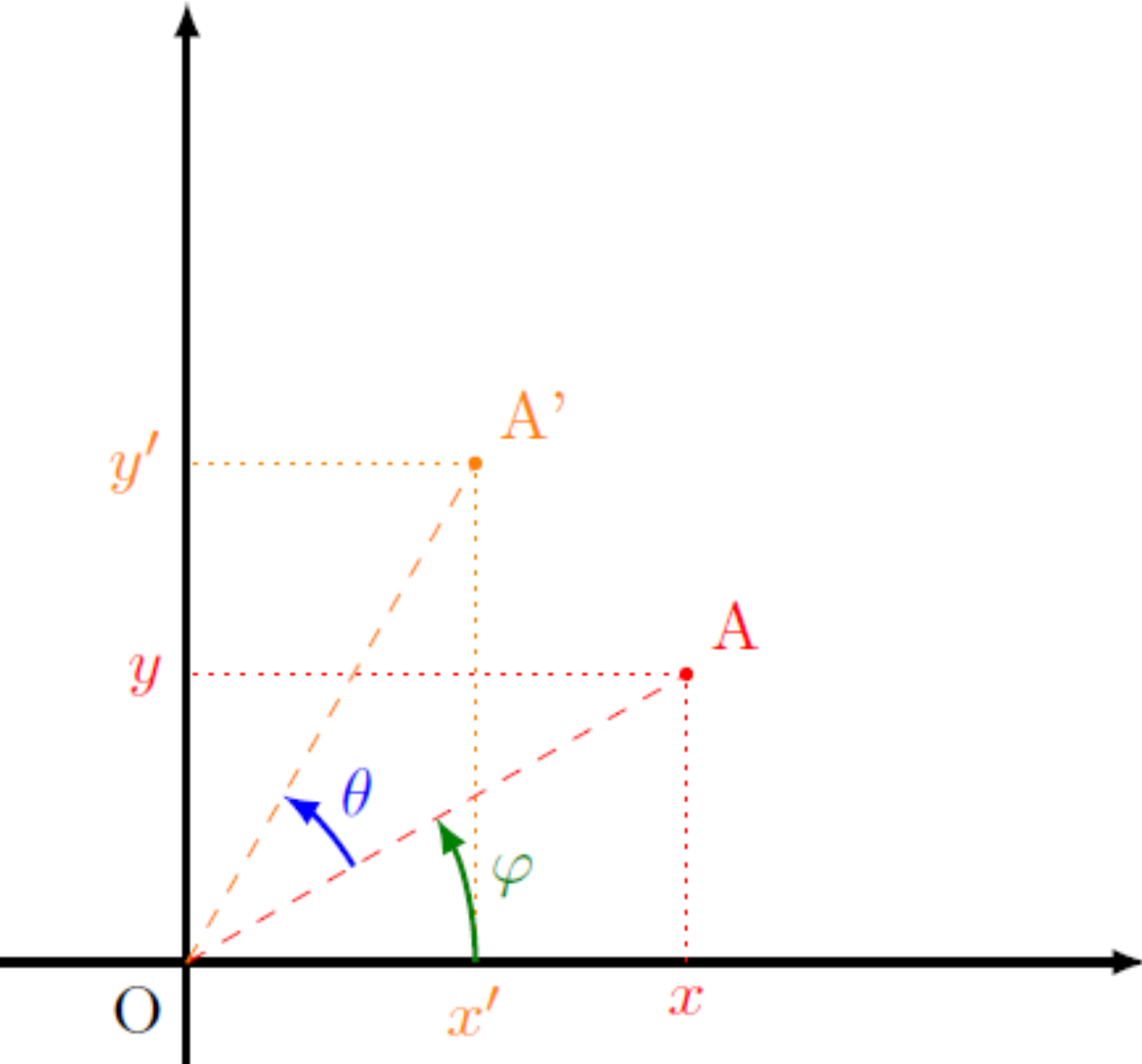
Question 1.1 : Coordonnées Polaires

Rappelez-vous, comment peut-on aussi décrire la position de ce point $A$ en utilisant des coordonnées polaires $(r, \phi)$ ? Quelles sont les relations entre les coordonnées cartésiennes $(x, y)$ et les coordonnées polaires $(r, \phi)$ ? Exprimez $x$ et $y$ en fonction de $r$ et $\phi$.

Indice : Pensez à la trigonométrie dans un triangle rectangle formé par le point $A$, sa projection sur l'axe des x, et l'origine.

Question 2.1 : Rotation et Coordonnées Polaires

Si on effectue une rotation d'angle $\theta$ autour de l'origine sur le point $A$, obtenant un nouveau point $A'$, comment la rotation affecte-t-elle les coordonnées polaires de $A$ ? Si les coordonnées polaires de $A$ sont $(r, \phi)$, quelles seront les coordonnées polaires $(r', \phi')$ du point $A'$ après une rotation d'angle $\theta$ ?

Indice : Une rotation autour de l'origine modifie-t-elle la distance à l'origine ? Qu'advient-il de l'angle polaire ?

Question 3.1 : Formules Trigonométriques

Pour relier $x'$ et $y'$ aux coordonnées initiales $(x, y)$, nous allons utiliser les formules d'addition d'angles en trigonométrie. Rappelez-vous et écrivez les formules pour $\cos(\phi+\theta)$ et $\sin(\phi+\theta)$ en fonction de $\cos(\phi)$, $\cos(\theta)$, $\sin(\phi)$ et $\sin(\theta)$.

Indice : Ces formules sont fondamentales en trigonométrie et expriment le cosinus et le sinus d'une somme d'angles.

Question 4.1 : Substitution et Simplification

Substituez les expressions de $\cos(\phi+\theta)$ et $\sin(\phi+\theta)$ dans les équations pour $x'$ et $y'$ que nous avons établies précédemment. Puis, utilisez les relations $x = r \cos(\phi)$ et $y = r \sin(\phi)$ pour exprimer $x'$ et $y'$ en fonction de $x$, $y$, $\cos(\theta)$ et $\sin(\theta)$.

Indice : Le but est d'éliminer les coordonnées polaires $r$ et $\phi$ au profit des coordonnées cartésiennes initiales $x$ et $y$.

Question 5.1 : Formulation Matricielle

Réécrivez le système d'équations que vous venez d'obtenir sous forme matricielle. Vous devriez obtenir une expression de la forme : $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = R(\theta) \begin{pmatrix} x \\ y \end{pmatrix} $$ où $R(\theta)$ est une matrice 2x2. Identifiez les éléments de la matrice $R(\theta)$ en comparant avec les équations pour $x'$ et $y'$.

Indice : Rappelez-vous comment la multiplication matricielle est définie pour retrouver les équations que vous avez établies.
Application : Utiliser la matrice de rotation $R(45^\circ)$ pour trouver les coordonnées du point $P'$ obtenu en rotant le point $P = (1, 0)$ de 45° autour de l'origine. Illustrer graphiquement.

Correction Guidée :

Démonstration de la forme de la matrice de rotation 2D :

Pour établir la matrice de rotation 2D, nous allons suivre une démarche pas à pas. Considérons un point $A$ du plan avec les coordonnées cartésiennes $(x, y)$.

Question 1.1 : Coordonnées Polaires

Rappelez-vous, comment peut-on aussi décrire la position de ce point $A$ en utilisant des coordonnées polaires $(r, \phi)$ ? Quelles sont les relations entre les coordonnées cartésiennes $(x, y)$ et les coordonnées polaires $(r, \phi)$ ? Exprimez $x$ et $y$ en fonction de $r=OA$ et $\phi$.

Indice : Pensez à la trigonométrie dans un triangle rectangle formé par le point $A$, sa projection sur l'axe des x, et l'origine.

Comme vous l'avez rappelé, les relations entre coordonnées cartésiennes et polaires sont : $$ x = OA \cos(\phi), \quad y = OA \sin(\phi) $$ où $OA$ représente la distance de l'origine à $A$, et $\phi$ est l'angle entre l'axe des x et le vecteur $\overrightarrow{OA}$.

Question 2.1 : Rotation et Coordonnées Polaires

Si on effectue une rotation d'angle $\theta$ autour de l'origine sur le point $A$, obtenant un nouveau point $A'$, comment la rotation affecte-t-elle les coordonnées polaires de $A$ ? Si les coordonnées polaires de $A$ sont $(r, \phi)$, quelles seront les coordonnées polaires $(r', \phi')$ du point $A'$ après une rotation d'angle $\theta$ ?

Indice : Une rotation autour de l'origine modifie-t-elle la distance à l'origine ? Qu'advient-il de l'angle polaire ?

Effectuer une rotation d'angle $\theta$ autour de l'origine revient à conserver la distance à l'origine $OA$ et à ajouter l'angle $\theta$ à l'angle polaire $\phi$. Donc, le point $A'$, image de $A$ par la rotation d'angle $\theta$, aura pour coordonnées polaires $(r'=OA', \phi+\theta)$. Notons $(x', y')$ les coordonnées cartésiennes de $A'$. Alors, en utilisant les relations entre coordonnées polaires et cartésiennes : $$ x' = OA' \cos(\phi+\theta), \quad y' = OA' \sin(\phi+\theta) $$

Question 3.1 : Formules Trigonométriques

Pour relier $x'$ et $y'$ aux coordonnées initiales $(x, y)$, nous allons utiliser les formules d'addition d'angles en trigonométrie. Rappelez-vous et écrivez les formules pour $\cos(\phi+\theta)$ et $\sin(\phi+\theta)$ en fonction de $\cos(\phi)$, $\cos(\theta)$, $\sin(\phi)$ et $\sin(\theta)$.

Indice : Ces formules sont fondamentales en trigonométrie et expriment le cosinus et le sinus d'une somme d'angles.

Utilisons les formules trigonométriques pour $\cos(\phi+\theta)$ et $\sin(\phi+\theta)$ : $$ \cos(\phi+\theta) = \cos(\phi)\cos(\theta) - \sin(\phi)\sin(\theta) $$ $$ \sin(\phi+\theta) = \sin(\phi)\cos(\theta) + \cos(\phi)\sin(\theta) $$

Question 4.1 : Substitution et Simplification

Substituez les expressions de $\cos(\phi+\theta)$ et $\sin(\phi+\theta)$ dans les équations pour $x'$ et $y'$ que nous avons établies précédemment. Puis, utilisez les relations $x = OA \cos(\phi)$ et $y = OA \sin(\phi)$ pour exprimer $x'$ et $y'$ en fonction de $x$, $y$, $\cos(\theta)$ et $\sin(\theta)$.

Indice : Le but est d'éliminer les coordonnées polaires $r$ et $\phi$ au profit des coordonnées cartésiennes initiales $x$ et $y$.

Substituons ces expressions dans les formules pour $x'$ et $y'$ : $$ x' = OA' (\cos(\phi)\cos(\theta) - \sin(\phi)\sin(\theta)) = (OA' \cos(\phi))\cos(\theta) - (OA' \sin(\phi))\sin(\theta) $$ $$ y' = OA' (\sin(\phi)\cos(\theta) + \cos(\phi)\sin(\theta)) = (OA' \sin(\phi))\cos(\theta) + (OA' \cos(\phi))\sin(\theta) $$

En utilisant $x = OA \cos(\phi)$ et $y = OA \sin(\phi)$, et sachant que $OA' = OA = r$ (rotation conserve la distance à l'origine), on obtient : $$ x' = x \cos(\theta) - y \sin(\theta) $$ $$ y' = x \sin(\theta) + y \cos(\theta) $$

Question 5.1 : Formulation Matricielle

Réécrivez le système d'équations que vous venez d'obtenir sous forme matricielle. Vous devriez obtenir une expression de la forme : $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = R(\theta) \begin{pmatrix} x \\ y \end{pmatrix} $$ où $R(\theta)$ est une matrice 2x2. Identifiez les éléments de la matrice $R(\theta)$ en comparant avec les équations pour $x'$ et $y'$.

Indice : Rappelez-vous comment la multiplication matricielle est définie pour retrouver les équations que vous avez établies.

On peut écrire ces relations sous forme matricielle : $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} $$

Conclusion pour la question 1 : La matrice de rotation 2D d'angle $\theta$ est donc bien donnée par : $$ R(\theta) = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} $$
Application avec $R(45^\circ)$ et $P = (1, 0)$ :

Pour une rotation de 45°, on a $\theta = 45^\circ = \frac{\pi}{4}$ radians. On sait que $\cos(45^\circ) = \sin(45^\circ) = \frac{\sqrt{2}}{2}$. Donc, la matrice de rotation d'angle 45° est : $$ R(45^\circ) = \begin{pmatrix} \cos(45^\circ) & -\sin(45^\circ) \\ \sin(45^\circ) & \cos(45^\circ) \end{pmatrix} = \begin{pmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix} $$

Le point $P = (1, 0)$ est représenté par le vecteur colonne $\begin{pmatrix} 1 \\ 0 \end{pmatrix}$. Pour trouver les coordonnées de $P'$, point obtenu en rotant $P$ de 45° autour de l'origine, on effectue le produit matriciel : $$ P' = R(45^\circ) P = \begin{pmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} (\frac{\sqrt{2}}{2} \times 1) + (-\frac{\sqrt{2}}{2} \times 0) \\ (\frac{\sqrt{2}}{2} \times 1) + (\frac{\sqrt{2}}{2} \times 0) \end{pmatrix} = \begin{pmatrix} \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} \end{pmatrix} $$

Donc, les coordonnées de $P'$ sont $\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$.

Illustration graphique :

Le point $P = (1, 0)$ est sur l'axe des x, à distance 1 de l'origine. Une rotation de 45° dans le sens trigonométrique (sens inverse des aiguilles d'une montre) va déplacer $P$ sur le cercle unité, dans la direction faisant un angle de 45° avec l'axe des x. Les coordonnées de $P'$ sont bien $(\cos(45^\circ), \sin(45^\circ)) = \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$. On peut visualiser cette rotation sur un graphique (voir l'image fournie dans l'énoncé).

Conclusion pour la question 2 : Les coordonnées du point $P'$ obtenu en rotant $P = (1, 0)$ de 45° autour de l'origine sont $P' = \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right)$.

Exercices : Matrices - Terminale Expertes pour aller plus loin

Matrices : Entraînement Terminale Maths Expertes

1. Définition et Opérations de Base

2. Inversibilité d'une Matrice et Déterminant

3. Puissances de Matrices : Techniques de Calcul Malin

4. Matrices Spéciales : Nilpotentes, Stochastiques, et de Rotation

Exercice 1 - Matrices Commutantes

Exercice 2 - Matrices Annulateurs et Inversibilité

Exercice 3 - Produit Matriciel Non Commutatif

Exercice 4 - Puissance $n$-ième d'une Matrice par Récurrence

Exercice 5 - Puissance $n$-ième et Binôme de Newton

Exercice 6 - Puissance $n$-ième et Division Euclidienne de Polynômes

Exercice 7 - Système 3x3, Inversibilité et Pivot de Gauss

Exercice 8 - Inverser une Matrice à Partir d'une Égalité

Exercice 9 - Calcul d'Inverse par Pivot de Gauss

Exercice 10 - Inversibilité de \(I_n - A\) pour Matrice Nilpotente \(A\)

Exercice 11 - Matrices Stochastiques et Stabilité par Produit

Exercice 12 - Matrices de Rotation 2D