Nombres Complexes : Géométrie
Revoyons ensemble les points essentiels sur la Géométrie des Nombres Complexes avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Affixe d'un Point et d'un Vecteur
Affixe d'un Point : Dans le plan complexe, chaque point $M(x, y)$ a une affixe $z = x + iy$. L'origine $O$ a pour affixe $0$.
Affixe d'un Vecteur : Le vecteur $\overrightarrow{AB}$ a pour affixe $z_B - z_A$, où $z_A$ et $z_B$ sont les affixes des points $A$ et $B$ respectivement.
2. Module et Argument Géométriquement
Module $|z|$ : Représente la distance $OM$, où $M$ est le point d'affixe $z$. C'est la longueur du vecteur $\overrightarrow{OM}$.
Argument $\arg(z)$ : Est l'angle $(\vec{u}, \overrightarrow{OM})$, où $\vec{u}$ est le vecteur unitaire de l'axe réel. Il est défini à $2\pi$ près.
3. Interprétations Géométriques des Opérations
Module du Produit $|z_1 z_2| = |z_1| |z_2|$ : La longueur du vecteur correspondant au produit est le produit des longueurs.
Argument du Produit $\arg(z_1 z_2) = \arg(z_1) + \arg(z_2) \pmod{2\pi}$ : Les angles s'additionnent lors de la multiplication.
Module du Quotient $|\frac{z_1}{z_2}| = \frac{|z_1|}{|z_2|}$ : La longueur du vecteur correspondant au quotient est le quotient des longueurs.
Argument du Quotient $\arg(\frac{z_1}{z_2}) = \arg(z_1) - \arg(z_2) \pmod{2\pi}$ : Les angles se soustraient lors de la division.
4. Distance et Alignement
Distance entre deux points A et B : $AB = |z_B - z_A|$.
Alignement de trois points A, B, C : Les points A, B, C sont alignés si et seulement si $\frac{z_C - z_A}{z_B - z_A}$ est un nombre réel.
5. Nature des Quadrilatères
Parallélogramme ABCD : $\overrightarrow{AB} = \overrightarrow{DC}$, ce qui se traduit par $z_B - z_A = z_C - z_D$.
Carré, Rectangle, Losange : Peuvent être identifiés en utilisant les longueurs des côtés (modules) et les angles (arguments) pour vérifier les propriétés géométriques (côtés égaux, angles droits, etc.).
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1 : Affixes et placement de points
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$.
1. Déterminer l'affixe des points A, B et C sur le graphique suivant :
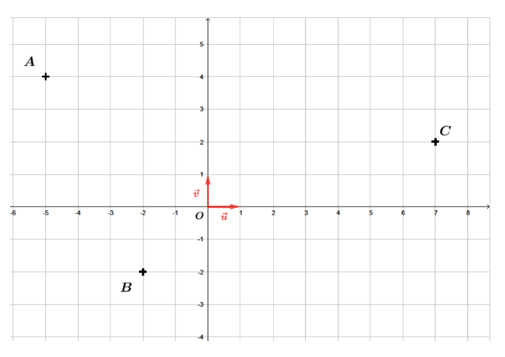
2. Placer les points D, E, F et G d'affixes respectives :
a. $z_D = -2 + i$
b. $z_E = 3 - 2i$
c. $z_F = -4i$
d. $z_G = 2$
3. Donner les affixes des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$.
Exercice 2 : Affixes de vecteurs
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$.
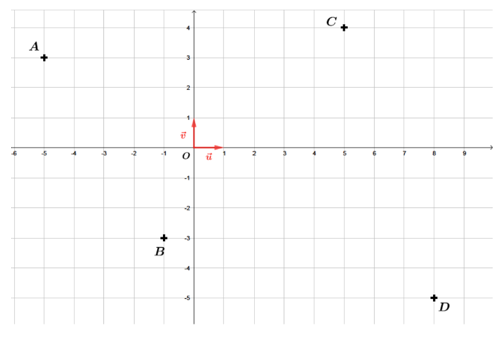
Donner les affixes des vecteurs $\overrightarrow{AB}$, $\overrightarrow{AC}$ et $\overrightarrow{CD}$.
Exercice 3 : Affixe de points et vecteurs
1. Placer dans un plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$ les points A, B, C et D d'affixes respectives :
$z_A = -2 + i$
$z_B = 1 + 2i$
$z_C = 4$
$z_D = -2i$
2. Déterminer l'affixe des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$.
Exercice 4 : Coordonnées et affixes
1. Déterminer les affixes des points de coordonnées suivantes dans le plan complexe :
E(2, -3), F(0, 4), G(-1, 5), H(3, 0).
2. Déterminer l'affixe des vecteurs $\overrightarrow{EF}$ et $\overrightarrow{HG}$.
Exercice 5 : Nature d'un quadrilatère
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$.
Soient les points A, B, C et D d'affixes respectives $z_A = -1 - i$, $z_B = 2 - 2i$, $z_C = 3 + i$ et $z_D = -2 + 2i$.
1. Placer les points A, B, C et D.
2. Déterminer les affixes des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$.
3. Que peut-on en déduire quant à la nature du quadrilatère ABCD ?
Exercice 6 : Centre d'un parallélogramme
On considère le parallélogramme ABCD de l'exercice 5.
1. On note I le centre du parallélogramme. Déterminer l'affixe $z_I$ du point I.
2. Vérifier que $z_I$ est aussi l'affixe du milieu de [AC] et du milieu de [BD].
Exercice 7 : Points alignés
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$.
Soient les points A, B et C d'affixes respectives $z_A = -2$, $z_B = 1 + i$ et $z_C = 4 + 2i$.
1. Calculer $\frac{z_C - z_A}{z_B - z_A}$.
2. Que peut-on en déduire sur l'alignement des points A, B et C ?
Exercice 8 : Centre de gravité
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$.
Soient les points A, B et C d'affixes respectives $z_A = 1 - 2i$, $z_B = -2 + i$ et $z_C = 4 + 3i$.
1. Placer les points A, B et C.
2. Déterminer l'affixe du centre de gravité G du triangle ABC.
On rappelle que le centre de gravité G vérifie la relation vectorielle : $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \vec{0}$.
Exercice 9 : Calcul de modules
Calculer le module de chacun des nombres complexes suivants : a. $z_1 = 3 + 4i$ b. $z_2 = -2 + 5i$ c. $z_3 = 1 - i\sqrt{3}$ d. $z_4 = -5i$ e. $z_5 = -7$
Exercice 10 : Module d'un produit
Calculer le module de chacun des nombres complexes suivants :
a. $z_1 = (1 + i)(3 - 2i)$
b. $z_2 = (2 + 2i)(1 - i)^2$
c. $z_3 = (4 - 3i)(-1 + i\sqrt{3})$
Exercice 11 : Module d'un quotient
Calculer le module de chacun des nombres complexes suivants :
a. $z_1 = \frac{2+i}{1-i}$
b. $z_2 = \frac{4-3i}{2+i}$
c. $z_3 = \frac{(1+i)^3}{2-i}$
Exercice 12 : Module d'une puissance
Calculer le module de chacun des nombres complexes suivants : a. $z_1 = (2-3i)^4$ b. $z_2 = (\sqrt{3} + i)^7$ c. $z_3 = (\frac{1+i}{2-i})^5$
Exercice 13 : Triangle rectangle
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$. Soient les points A, B et C d'affixes respectives $z_A = 1 + i$, $z_B = -2 + 3i$ et $z_C = -1 - 2i$.
1. Calculer les distances AB, AC et BC.
2. En déduire la nature du triangle ABC.
Exercice 14 : Argument d'un nombre complexe
Déterminer un argument des nombres complexes suivants :
a. $z_1 = -2$
b. $z_2 = 3i$
c. $z_3 = 1 + i$
d. $z_4 = -\sqrt{3} + i$
Exercice 15 : Argument et lieu géométrique
Déterminer l'ensemble des points M d'affixe $z$ tels que :
1. $\arg(z) = \frac{\pi}{2} \pmod{2\pi}$
2. $\arg(z) = -\frac{3\pi}{4} \pmod{2\pi}$
Exercice 16 : Argument d'un produit
Soient $z_1 = 2e^{i\frac{\pi}{4}}$ et $z_2 = 3e^{i\frac{2\pi}{3}}$.
Déterminer un argument du produit $z_1 z_2$.
Exercice 17 : Argument d'un quotient
Soient $z_1 = 4e^{i\frac{\pi}{6}}$ et $z_2 = 2e^{i\frac{3\pi}{4}}$.
Déterminer un argument du quotient $\frac{z_1}{z_2}$.
Exercice 18 : Forme trigonométrique
Écrire les nombres complexes suivants sous forme trigonométrique :
a. $z_1 = -3$
b. $z_2 = 4i$
c. $z_3 = 2 + 2i$
d. $z_4 = -1 + i\sqrt{3}$
Exercice 19 : Forme algébrique à partir de la forme trigonométrique
Déterminer la forme algébrique des nombres complexes suivants :
a. $z_1 = 3(\cos(\frac{\pi}{6}) + i\sin(\frac{\pi}{6}))$
b. $z_2 = 2(\cos(\frac{3\pi}{4}) + i\sin(\frac{3\pi}{4}))$
c. $z_3 = 5(\cos(\pi) + i\sin(\pi))$
Exercice 20 : Conjugué et forme trigonométrique
Soit $z = r(\cos(\theta) + i\sin(\theta))$ un nombre complexe sous forme trigonométrique, avec $r > 0$.
1. Déterminer la forme trigonométrique du conjugué $\bar{z}$.
2. Déterminer la forme trigonométrique de $-z$.
3. Déterminer la forme trigonométrique de $\frac{1}{z}$ (pour $z \neq 0$).
Exercice 21 : Module et argument d'un inverse
Soit $z = 2 + 2i$.
1. Déterminer le module et un argument de $z$.
2. En déduire le module et un argument de $\frac{1}{z}$.
Exercice 22 : Forme exponentielle et opérations
Soient $z_1 = 2e^{i\frac{\pi}{3}}$ et $z_2 = 3e^{-i\frac{\pi}{4}}$.
1. Déterminer la forme exponentielle de $z_1 z_2$.
2. Déterminer la forme exponentielle de $\frac{z_1}{z_2}$.
3. Déterminer la forme exponentielle de $z_1^4$.
Exercice 23 : Conjugué et argument
Soit $z$ un nombre complexe non nul d'argument $\theta$.
1. Exprimer l'argument de $-z$ en fonction de $\theta$.
2. Exprimer l'argument de $\bar{z}$ en fonction de $\theta$.
3. Exprimer l'argument de $\frac{1}{z}$ en fonction de $\theta$.
Exercice 24 : Forme trigonométrique et argument
On considère le nombre complexe $z = \frac{1 + i\sqrt{3}}{1 - i}$.
1. Écrire $1 + i\sqrt{3}$ et $1 - i$ sous forme trigonométrique.
2. En déduire la forme trigonométrique de $z$.
3. Déterminer un argument de $z$.
Exercice 25 : Forme exponentielle et argument
On considère le nombre complexe $z = \frac{-2i}{1 + i}$.
1. Écrire $-2i$ et $1+i$ sous forme exponentielle.
2. En déduire la forme exponentielle de $z$.
3. Déterminer un argument de $z$.
Exercice 26 : Module et argument d'une puissance
Soit $z = 1 - i$.
1. Déterminer le module et un argument de $z$.
2. En déduire le module et un argument de $z^{10}$.
Exercice 27 : Forme exponentielle et équations
1. Écrire sous forme exponentielle les solutions dans $\mathbb{C}$ de l'équation $z^4 = 1$.
2. Représenter les images des solutions dans le plan complexe.
Exercice 28 : Module et alignement
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$.
Soient les points A, B et C d'affixes respectives $z_A = 2$, $z_B = 1 + i\sqrt{3}$ et $z_C = 4$.
1. Calculer les distances OA, OB et OC.
2. Que peut-on en déduire sur la position des points A, B et C par rapport à O ?
Exercice 29 : Calcul d'une distance
Dans le plan complexe, on considère les points A et B d'affixes respectives $z_A = 3 - i$ et $z_B = 1 + 2i$.
Calculer la distance AB.
Exercice 30 : Triangle équilatéral
On travaille dans le plan complexe rapporté au repère orthonormal direct $(O;\vec{u},\vec{v})$.
Soient les points A, B et C d'affixes respectives $z_A = 2$, $z_B = 1 + i\sqrt{3}$ et $z_C = 1 - i\sqrt{3}$.
1. Montrer que le triangle ABC est équilatéral.
2. Déterminer l'affixe du centre de gravité du triangle ABC.
Exercice 31 : Suite de modules
Soit la suite $(z_n)$ définie par $z_0 = 3 + 3i$ et pour tout entier naturel $n$, $z_{n+1} = \frac{\sqrt{3} + i}{2}z_n$.
On pose $u_n = |z_n|$ pour tout $n$.
1. Montrer que la suite $(u_n)$ est une suite géométrique dont on précisera la raison et le premier terme.
2. Déterminer l'expression de $u_n$ en fonction de $n$.
3. Écrire un script Python qui affiche les 10 premiers termes de la suite $(u_n)$.
4. Tester le script avec l'application suivante :
Exercice 32 : Suite d'arguments
Soit la suite $(z_n)$ définie par $z_0 = e^{i\frac{\pi}{6}}$ et pour tout entier naturel $n$, $z_{n+1} = \frac{1 + i}{2}z_n$.
On pose $\theta_n = \arg(z_n)$.
1. Montrer que la suite $(\theta_n)$ est une suite arithmético-géométrique et déterminer sa raison et son premier terme.
2. Exprimer $\theta_n$ en fonction de $n$.
3. Écrire un script Python qui affiche les 10 premiers termes de la suite $(\theta_n)$.
4. Tester le script avec l'application suivante :
Exercice 33 : Module et argument d'une puissance
Soit $z = \sqrt{3} - i$.
1. Déterminer le module et un argument de $z$.
2. En déduire le module et un argument de $z^6$.
3. Écrire un script Python qui calcule et affiche le module et un argument de $z^n$ pour $n$ allant de 1 à 8.
4. Tester le script avec l'application suivante :
Exercice 34 : Forme exponentielle et calcul de cosinus et sinus
Soient $z_1 = 1 + i$ et $z_2 = \sqrt{3} - i$.
1. Écrire $z_1$ et $z_2$ sous forme exponentielle.
2. En déduire la forme exponentielle de $\frac{z_1}{z_2}$.
3. Déterminer la forme algébrique de $\frac{z_1}{z_2}$.
4. En déduire les valeurs exactes de $\cos(\frac{5\pi}{12})$ et $\sin(\frac{5\pi}{12})$.
Exercice 35 : Une suite complexe
On considère la suite de nombres complexes $(z_n)$ définie par $z_0 = 1$ et pour tout entier naturel $n$, $z_{n+1} = \frac{1}{2}(z_n + |z_n|)$.
1. Calculer $z_1$, $z_2$ et $z_3$ sous forme algébrique.
2. Que peut-on conjecturer sur la suite $(|z_n|)$ ?
3. Démontrer cette conjecture par récurrence.
4. Écrire un script Python qui affiche les 10 premiers termes de la suite $(z_n)$.
5. Tester le script avec l'application suivante :