Module d'un Nombre Complexe
Le module d'un nombre complexe est un concept fondamental en mathématiques. Il représente la distance entre l'origine du plan complexe et le point représentant ce nombre. Maîtriser le calcul et l'interprétation du module est essentiel pour résoudre de nombreux problèmes.
Revoyons ensemble les points essentiels sur le module d'un nombre complexe avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Définition du module
Soit $z = a + bi$ un nombre complexe, où $a$ et $b$ sont des nombres réels et $i$ est l'unité imaginaire ($i^2 = -1$).
Le module de $z$, noté $|z|$, est défini par :
$$|z| = \sqrt{a^2 + b^2}$$
Le module représente la distance entre l'origine $(0,0)$ et le point $(a, b)$ dans le plan complexe.
2. Interprétation géométrique
Dans le plan complexe, le module $|z|$ correspond à la longueur du segment reliant l'origine au point d'affixe $z$.
Si $z_A$ et $z_B$ sont les affixes de deux points A et B, alors $|z_B - z_A|$ représente la distance entre les points A et B.
3. Propriétés du module
Pour tous nombres complexes $z$ et $z'$ :
$|z| \geq 0$
$|z| = 0$ si et seulement si $z = 0$
$|z \cdot z'| = |z| \cdot |z'|$
$\left|\frac{z}{z'}\right| = \frac{|z|}{|z'|}$ (si $z' \neq 0$)
$|-z| = |\overline{z}| = |z|$ (où $\overline{z}$ est le conjugué de $z$)
Inégalité triangulaire : $|z + z'| \leq |z| + |z'|$
4. Module et cercle
L'ensemble des points M d'affixe $z$ tels que $|z - z_0| = r$, où $z_0$ est un nombre complexe et $r$ un réel positif, est le cercle de centre le point d'affixe $z_0$ et de rayon $r$.
5. Module et médiatrice
L'ensemble des points M d'affixe $z$ tels que $|z - z_A| = |z - z_B|$, où $z_A$ et $z_B$ sont deux nombres complexes distincts, est la médiatrice du segment [AB], où A et B sont les points d'affixes respectives $z_A$ et $z_B$.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
Calculer le module des nombres complexes suivants :
- $z_1 = 4 + 3i$
- $z_2 = -1 + 2i$
- $z_3 = -3 - 4i$
- $z_4 = 5 - i$
Exercice 2
On considère la figure suivante:
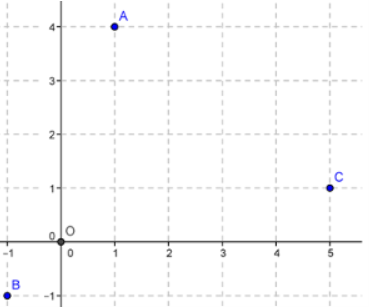
1) À l'aide d'un compas, déterminer une valeur approchée des longueurs OA, OB, OC, AB, AC et BC.
2) Lire les affixes $z_A$, $z_B$, $z_C$ des points A, B et C.
3) Déterminer $|z_A|$, $|z_B|$, $|z_C|$. Est-ce cohérent?
4) Déterminer $|z_C-z_A|$, $|z_B-z_A|$ et $|z_B-z_C|$. Est-ce cohérent?
5) Le triangle ABC est-il rectangle, isocèle ou équilatéral?
Exercice 3
Calculer le module de chaque nombre complexe suivant:
$z_1=3+3i$ $z_2=-\sqrt{3}+i$
$z_3=-\dfrac 25i$ $z_4=-6+6i\sqrt{3}$
Exercice 4
Calculer le module de chaque nombre complexe suivant:
$z_1=(5+2i)\left(\sqrt{ 3}+i\sqrt{6}\right)$ $z_2=
\left(\dfrac{\sqrt{3}-i}{4i}\right)^{\!\! 3}$
Exercice 5
Déterminer le module de $z$ dans chacun des cas suivants:
$a. z=2$
$b. z=-3$
$c. z=4i$
$d. z=\sqrt{3}+3i$
$e. z=\frac 2i$
$ f. z=\cos \frac {\pi}3-i\sin \frac {\pi}3$
Exercice 6
Démontrer que pour tout nombre complexe $z$, $|-z|=|\overline z|=|z|$.
Exercice 7
Soit $z_1=\sqrt 2 +i\sqrt 6$ et $z_2=2+2i$.
Déterminer les modules de $z_1$, $z_2$, $-\sqrt 2 -i\sqrt 6$, $2-2i$ et de
\[\frac{-\sqrt 2 -i\sqrt 6}{(2-2i)^2}\]
Exercice 8
1) Déterminer le module de $z_1=1-i\sqrt 3$ et $z_2=-1+i$.
2) Déterminer le module des nombres suivants, en utilisant si possible la question 1)
a. $\frac{-1+i\sqrt 3}{-1-i}$
b. $-\frac12(-1+i\sqrt 3)$
c. $\frac{(1-i\sqrt 3)^2}{(1-i)^3}$
d. $\frac 14-\frac 14i$
e. $z_1+z_2$
Exercice 9
Déterminer l'ensemble des points M d'affixe $z$ dans chacun des cas suivants:
a. $|z-3|=4$
b. $ |z+1-i|=3$
c. $ |z+2|=|z-2+3i|$
d. $|4-z|=|\overline z-1+2i|$
Exercice 10
Dans le plan muni d'un repère orthonormé, construire l'ensemble $\mathcal{S}$ des points M
dont l'affixe $z$ vérifie les deux conditions: $\left\{
\begin{array}{l}
|z-i|=|z+1| \\
|z+3-2i|\le 2
\end{array}
\right.$
Exercice 11
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
On note $\Gamma$ l'ensemble des points M dont l'affixe $z$ vérifie $|z-2-3i|=|z-4+i|$.
1) Justifier que le point $C(1;0)$ appartient à $\Gamma$.
2) Déterminer l'ensemble $\Gamma$ en posant $z=x+iy$ et le représenter.
3) Refaire la question 2) par une autre méthode.
Exercice 12
On considère les points A, B, C d'affixes respectives $z_A=-1-5i$, $z_B=7+i$ et $z_C=8-2i$.
1) Déterminer la nature du triangle ABC.
2) En déduire que A, B et C sont sur un même cercle. On note I le centre de ce cercle.
Déterminer l'affixe de I et le rayon de ce cercle.
3) Le point D(0;2) est-il également sur ce cercle? Justifier.
Exercice 13
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
À tout point $M$ d'affixe $z$ différente de $3i$, on associe le point $M'$ d'affixe
\[z'=\frac{z-2}{iz+3}\]
.Déterminer l'ensemble $\mathscr E$ des points M d'affixe $z$ tels que M' soit sur le cercle de centre O et de rayon 1.
Exercice 14
On considère les points A, B, C d'affixes respectives $z_A=\sqrt 3+2i$, $z_B=-\overline{z}_A$ et
$z_C=-i$.
1) On a placé le point A sur la figure ci-contre:
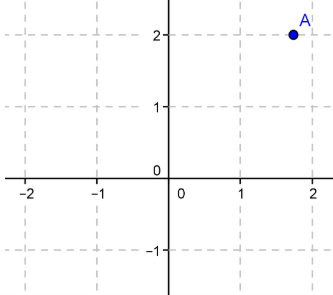
Placer les points B et C.
2) Démontrer que le triangle ABC est équilatéral.
3) Soit G, le centre de gravité du triangle ABC.
a) Placer le point G sur la figure
en faisant apparaitre les traits de construction.
b) Rappeler la définition vectorielle de G.
c) Déterminer $z_G$, l'affixe de G.
4) Soit I le milieu du segment [AG].
Déterminer $z_I$, l'affixe de I. Placer le point I sur la figure.
5) Soit J, le point tel que GIJC soit un parallélogramme. Déterminer $z_J$, l'affixe de J.
6) Démontrer que les droites (GJ) et (CJ) sont perpendiculaires.
7) En déduire que J est sur un cercle que l'on précisera. Placer J sur la figure.
Exercice 15
Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
On a placé un point $M$ d'affixe $z$ sur la figure ci-contre:
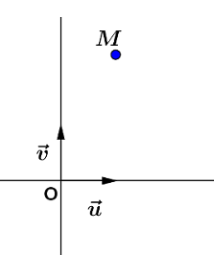
Soit $M'$ le point d'affixe
\[z'=\frac 12\left(\frac {z+|z|}2 \right)\]
.1) Construire le point $M'$ sur la figure en laissant les traits de construction.
2) On définit la suite de nombres complexes ($z_n$) de premier terme $z_0$
appartenant à $\mathbb{C}$ et pour tout entier naturel $n$:
\[z_{n+1}=\frac{z_n+|z_n|}4\]
.a) Que peut-on dire du comportement à l'infini de la suite ($|z_n|$) quand $z_0$ est un réel négatif?
b) Que peut-on dire du comportement à l'infini de la suite ($|z_n|$) quand $z_0$ est un réel positif?
c) On suppose désormais que $z_0$ n'est pas un nombre réel.
Que peut-on dire du comportement à l'infini de la suite ($|z_n|$)? Justifier.
Exercice 16
Quels sont les nombres complexes $z$ tels $z$, $\frac{1}{z}$ et $1-z$ aient même module?
Exercice 17
On considère la suite de nombres complexes $(z_n)$ définie par
$z_0=100$ et pour tout entier
naturel $n$, $z_{n+1}=\frac i3 z_n$.
Le plan est muni d'un repère orthonormé direct (O;$\vec u$;$\vec v$). Pour tout entier naturel $n$, on
note ${\rm M}_n$ le point d'affixe $z_n$. On rappelle qu'un disque de centre A et de rayon $r$, où $r$
est un réel positif, est l'ensemble des points M du plan tels que ${\rm AM}\le r$.
Démontrer qu'à partir d'un certain rang, tous les points ${\rm M_n}$ appartiennent au disque de centre
${\rm O}$ et de rayon $1$.
Exercice 18
Le plan complexe est muni d'un repère orthonormé ${(\rm O};\vec u;\vec v)$.
Gaspard affirme que l'équation $z^3-3z^2+3z=0$ admet trois solutions dans l'ensemble des nombres
complexes $\mathbb{C}$, qui sont les affixes de trois points formant un triangle équilatéral. Gaspard
a-t-il raison? Justifier.
Exercice 19
On considère dans $\mathbb{C}$ l'équation $(4z^2-20z+37)(2z-7+2i)=0$.
Nasser affirme que les solutions de cette équation sont les affixes de points appartenant à un même
cercle de centre $\rm P$ d'affixe 2. Nasser a-t-il raison? Justifier.
Exercice 20
On rappelle la régle du produit nul: $x.y=0 \Rightarrow x=0$ ou $y=0$
Cette règle qui est vraie avec des nombres réels, est-elle encore vraie avec des nombres complexes?
Exercice 21
On s'intéresse aux triplets d'entiers naturels non nuls $(x, y, z)$ tels que $x^2 + y^2 = z^2$.
Ces triplets sont nommés « triplets pythagoriciens » en référence aux triangles rectangles dont ils
mesurent les côtés.
Le but de cette question est de trouver un triplet pythagoricien à l'aide des nombres complexes.
On considère le nombre complexe $z=3+2i$.
a) Déterminer $z^2$ sous forme algébrique.
b) Déterminer $|z^2|$.
c) En déduire un triplet pythagoricien.Généraliser la méthode de la question 1. pour trouver une infinité de triplets pythagoriciens.