Matrices et Graphes Probabilistes
Révisions et exercices sur les matrices et graphes probabilistes.
Revoyons ensemble les points essentiels sur les Matrices et Graphes Probabilistes avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Graphe probabiliste et matrice de transition
Un graphe probabiliste est un graphe orienté pondéré dont les sommets représentent les états possibles d'un système et les arêtes les transitions possibles entre ces états. Les poids des arêtes représentent les probabilités de transition.
La matrice de transition $T$ d'un graphe probabiliste à $n$ états est une matrice carrée d'ordre $n$ où $T_{ij}$ est la probabilité de transition de l'état $i$ à l'état $j$. La somme des coefficients de chaque ligne d'une matrice de transition est toujours égale à 1.
Si on note $P_n = \begin{pmatrix} p_1 & p_2 & \cdots & p_n \end{pmatrix}$ la matrice ligne des probabilités des états à l'étape $n$, alors la matrice d'état à l'étape $n+1$ est donnée par :
$$P_{n+1} = P_n \times T$$2. Matrice d'état et évolution
La matrice d'état à l'étape $n$, notée $P_n$, est une matrice ligne dont le $i$-ème coefficient est la probabilité de se trouver dans l'état $i$ à l'étape $n$.
Si $P_0$ est la matrice d'état initial et $T$ la matrice de transition, alors la matrice d'état à l'étape $n$ est donnée par :
$$P_n = P_0 \times T^n$$3. État stable d'un graphe probabiliste
Un état stable (ou distribution stationnaire) est une matrice d'état $P = \begin{pmatrix} p_1 & p_2 & \cdots & p_n \end{pmatrix}$ telle que $P = P \times T$. En d'autres termes, si le système atteint l'état stable, les probabilités des états ne changent plus au fil des étapes.
Pour trouver l'état stable, on doit résoudre le système d'équations suivant :
$$P = P \times T$$ $$\sum_{i=1}^{n} p_i = 1$$4. Cas particulier des chaînes de Markov à deux états
Dans le cas d'un graphe probabiliste à deux états A et B, la matrice de transition est de la forme :
$$T = \begin{pmatrix} 1-a & a \\ b & 1-b \end{pmatrix}$$où $1-a$ est la probabilité de rester en A, $a$ de passer de A à B, $b$ de passer de B à A, et $1-b$ de rester en B.
L'état stable $P = \begin{pmatrix} x & y \end{pmatrix}$ se trouve en résolvant :
$$\begin{pmatrix} x & y \end{pmatrix} = \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} 1-a & a \\ b & 1-b \end{pmatrix}$$ $$x + y = 1$$Ce qui conduit au système :
$$x = x(1-a) + yb$$ $$y = xa + y(1-b)$$ $$x + y = 1$$On trouve alors :
$$x = \frac{b}{a+b} \quad \text{et} \quad y = \frac{a}{a+b}$$C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1: Matrice et graphe probabiliste
Un automate peut se trouver dans deux états ${\rm A}$ ou ${\rm B}$. À chaque seconde il peut soit rester dans l'état où il se trouve, soit en changer, avec des probabilités données par le graphe probabiliste ci-dessous.
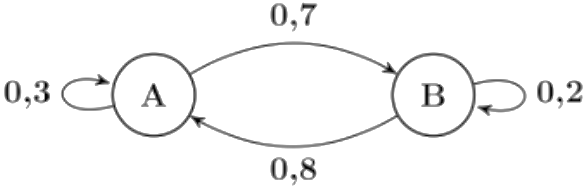
Pour tout entier naturel $n$, on note $a_n$ la probabilité que l'automate se trouve
dans l'état ${\rm A}$ après $n$ secondes et $b_n$ la probabilité que l'automate se trouve
dans l'état ${\rm B}$ après $n$ secondes.
Au départ, l'automate est dans l'état ${\rm B}$. Gaspard affirme qu'après 4 secondes, l'automate a autant de chances d'être dans
l'état $\rm A$ que d'être dans l'état $\rm B$.
Cette affirmation est-elle vraie?

Exercices 2: Matrices : suite du type $U_{n+1} =AU_n$
Des souris sont dans une cage comportant deux compartiments A et B. La porte entre ces compartiments est ouverte dix minutes tous les jours. Chaque jour 20% des souris du compartiment A passent dans le compartiment B et 10% des souris qui étaient dans le compartiment B passent dans le compartiment A. Pour tout entier naturel $n$, on note $a_{n}$ et $b_{n}$ les proportions de souris présentes respectivement dans les compartiments A et B après $n$ jours et on convient que $a_0 = b_0 =0,5$ et on note $U_{n}$ la matrice $\begin{pmatrix}a_{n}\\b_{n}\end{pmatrix}$.
-
Exprimer pour tout entier naturel $n$, $a_{n+1}$ et $b_{n+1}$ en fonction de $a_{n}$ et $b_{n}$.
Déterminer la matrice $A$ telle que pour tout entier naturel $n$, $U_{n+1} = AU_{n}$.
Montrer par récurrence que pour tout entier naturel $n$, $U_{n} = A^nU_{0}$.
On admet que pour tout entier naturel $n$, $A^n = \begin{pmatrix}\frac{1 +2 \times 0,7^n}{3}&\frac{1 - 0,7^n}{3}\\ \frac{2 - 2 \times 0,7^n}{3}&\frac{2 + 0,7^n}{3}\end{pmatrix}$.
Que peut-on dire de la répartition à long terme des souris dans les compartiments A et B ?

Exercices 3: Matrices et suites récurrentes linéaires d'ordre 2
Soit $(u_n)$ la suite définie pour tout entier naturel $n$ par : $u_0 = 0$, $u_1 = 1$ et $u_{n+2} = \frac{3}{2}u_{n+1} - \frac{1}{2}u_n$.
Pour tout entier naturel $n$, on pose : $U_n = \begin{pmatrix} u_{n+1} \\ u_{n}\end{pmatrix}$
-
Donner $U_0$ et $U_1$.
Déterminer la matrice $A$ telle que pour tout entier naturel $n$, on ait : $U_{n+1} = A U_n$.
Donner sans justifier pour tout entier naturel $n$, $U_n$ en fonction de $A$, $n$ et $U_0$.
-
On admet que pour tout entier naturel $n$, on a : $A^n = \dfrac{1}{2^n}\begin{pmatrix}2^{n+1}-1&-2^n+1\\2^{n+1}-2&-2^n+2\end{pmatrix}$.
En déduire, pour tout entier naturel $n$, l'expression de $u_n$ en fonction de $n$ puis donner la limite de la suite $(u_n)$.

Exercices 4: Matrices : une suite du type $U_{n+1} = AU_n + B$
Soit $(U_n)$ la suite de matrices de taille $(2~;~1)$ définie pour tout entier naturel $n$ par :
$U_0 = \begin{pmatrix}0\\1\end{pmatrix}$ et $U_{n+1} = AU_n + B$ avec $A = \begin{pmatrix}1/2&1\\0&1/2\end{pmatrix}$ et $B = \begin{pmatrix}1\\1\end{pmatrix}$
-
Calculer $A(I_2-A)$ et en déduire que la matrice $I_2-A$ est inversible. Donner $(I_2-A)^{-1}$.
Déterminer la matrice $L$ de taille $(2~;~1)$ qui vérifie $L = AL + B$.
Pour tout entier naturel, on pose $V_n = U_n - L$.
Montrer que pour tout entier naturel, $V_{n+1} = AV_n$.
En déduire une expression de $V_n$ puis de $U_n$ en fonction de $A$ et $n$.
On admet que la suite $(A^n)$ tend vers la matrice nulle d'ordre $2$ lorsque $n$ tend vers l'infini.
Que peut-on en déduire pour la suite $(U_n)$ ?

Exercices 5: Marches aléatoires : le cours à travers un exemple
Dans un pays imaginaire, s'il fait beau et sec un jour, il fera encore beau et sec avec une probabilité de $5/6$ le lendemain. Dans le cas contraire, il fera humide. S'il fait humide un jour, on convient également qu'il fera encore humide avec une probabilité de $2/3$ et qu'il fera beau et sec sinon. Aujourd'hui, il fait beau et sec.
On note:
$A_n$ l'événement : "il fait beau et sec dans $n$ jours"
$B_n$ l'événement : "il fait humide dans $n$ jours".
Calculer ${ \rm P}(A_n) = p_n$ et ${\rm P}(B_n) = q_n$ pour tout entier $n$.

Exercices 6: Marches aléatoires : un problème d'urnes
On dispose de deux urnes U et V contenant chacune deux boules. Au départ, l'urne U contient deux boules blanches et l'urne V contient deux boules noires.
On effectue des tirages successifs dans ces urnes de la façon suivante : chaque tirage consiste
à prendre au hasard, de manière simultanée, une boule dans chaque urne et à la mettre dans
l'autre urne.
Ce processus peut être vue comme une marche aléatoire sur un espace à trois états : $A$ : "il y a 0 boule blanche dans U", $B$ : "il y a 1 boule blanche dans U" et $C$ : "il y a 2 boules blanches dans U".
Représenter la situation à l'aide d'un graphe probabiliste.
-
Pour tout entier naturel $n$, on note $P_n$ la matrice d'état du système après $n$ tirages. On a donc en particulier $P_0 = \begin{pmatrix}0 & 0& 1\end{pmatrix}$. Déterminer la matrice de transition $T$ telle que pour tout entier naturel $n$, $P_{n+1} = P_nT$.
-
On admet que la suite de matrices $(P_n)$ converge vers une matrice d'état stable $P$ qui vérifie $P = PT$. Déterminer $P$ et interpréter.

Exercices 7: Marches aléatoires Bac S spé maths Polynésie 2016
Un mobile peut occuper deux positions $\rm A$ et $\rm B$. À chaque étape, il peut soit rester dans la
position dans laquelle il se trouve, soit en changer. Pour tout entier naturel $n$, on note :
${\rm A}_n$ l'évènement « le mobile se trouve dans la position A à l'étape $n$ » et $a_n$ sa probabilité.
${\rm B}_n$ l'évènement « le mobile se trouve dans la position B à l'étape $n$ » et $b_n$ sa probabilité.
$\rm{X}_n$ la matrice colonne $\begin{pmatrix}
a_n \\
b_n
\end{pmatrix}$.
On admet que, pour tout entier naturel $n$, $\rm{X}_{n+1}={\rm M}\times \rm{X}_n$ avec ${\rm M}=\begin{pmatrix}
0,55 ~& 0,3 \\
0,45 & 0,7
\end{pmatrix}$.
Déterminer la probabilité de ${{\rm P_A}}_n({\rm B}_{n+1})$.
Existe-t-il un état initial $\rm{X}_0 = \begin{pmatrix} a_0 \\ b_0 \end{pmatrix}$ tel que la probabilité d'être en $\rm B$ à l'étape 1 est trois fois plus grande que celle d'être en $\rm A$ à l'étape 1, autrement dit tel que $b_1=3a_1$?

Exercices 8: Marches aléatoires sur un triangle Bac S spé maths Métropole 2015
Une boîte contient 3 jetons rouges, 4 verts et 18 blancs. On considère la marche aléatoire d'un pion (au départ en A) sur un triangle ABC.
À chaque étape, on tire au hasard un des jetons puis on le remet dans la boîte.
$\bullet~~$Lorsqu'on est en A, si le jeton tiré est rouge, le pion va en B, vert en C, blanc reste en A.
$\bullet~~$Lorsqu'on est en B, si le jeton tiré est rouge, le pion va en A, vert en C, blanc reste en B.
$\bullet~~$Lorsqu'on est en C, si le jeton tiré est rouge, le pion va en A, vert en B, blanc reste en C.
Pour tout entier naturel $n$, on note $a_n$, $b_n$ et $c_n$ les probabilités que le pion soit respectivement sur les sommets A, B et C à l'étape $n$. On note $X_n$ la matrice ligne $\begin{pmatrix}a_n& b_n& c_n\end{pmatrix}$.
Déterminer la matrice $T$ telle que pour tout entier naturel $n$, $X_{n+1} = X_nT$.
On admet que $T = PDP^{-1}$ où $P = \begin{pmatrix}1&7&4\\ 1&-3&4\\1&-3&-7\end{pmatrix}$ et $D = \begin{pmatrix}1&0&0&\\0&0,6&0\\0&0&0,56\end{pmatrix}$.
Montrer que pour tout entier naturel $n$, $T^n = PD^nP^{-1}$.
Donner sans justification les coefficients de la matrice $D^n$.
On note $\alpha_n,\:\beta_n,\:\gamma_n$ les coefficients de la première ligne de la matrice $T^n$ et on admet que :
$\displaystyle \alpha_n = \frac{3}{10} + \frac{7}{10} \times 0,6^n$ et $\displaystyle \beta_n = \frac{37 - 77 \times 0,6^n + 40 \times 0,56^n}{110}$.
On rappelle que, pour tout entier naturel $n$, $X_n = X_0T^n$.
Déterminer les nombres $a_n$, $b_n$, à l'aide des coefficients $\alpha_n$ et $\beta_n$. En déduire $c_n$.
Déterminer les limites des suites $\left(a_n\right)$, $\left(b_n\right)$ et $\left(c_n\right)$.
Sur quel sommet a-t-on le plus de chance de se retrouver après un grand nombre d'étapes ?
