Exercices - Nombres Complexes et Géométrie

Revoyons ensemble les points essentiels sur Nombres Complexes et Géométrie avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !

1. Affixe d'un point et d'un vecteur

Dans le plan complexe, à chaque point M, on peut associer un unique nombre complexe $z$, appelé son affixe. Réciproquement, à chaque nombre complexe, on peut associer un unique point du plan complexe.

Si un point M a pour coordonnées $(x;y)$ dans le plan muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$, alors son affixe est $z = x + iy$.

De même, à tout vecteur $\overrightarrow{AB}$ du plan, on peut associer un affixe, qui est l'affixe du point image de $\overrightarrow{AB}$ par la translation qui transforme O en A.

Si $A$ a pour affixe $z_A$ et $B$ a pour affixe $z_B$, alors l'affixe du vecteur $\overrightarrow{AB}$ est donné par :

$$z_{\overrightarrow{AB}} = z_B - z_A$$

2. Opérations sur les affixes et interprétation géométrique

Somme de vecteurs : L'affixe de la somme de deux vecteurs $\overrightarrow{u} + \overrightarrow{v}$ est la somme des affixes de $\overrightarrow{u}$ et $\overrightarrow{v}$.

Produit par un scalaire : L'affixe du vecteur $k\overrightarrow{u}$ (où $k$ est un nombre réel) est $k$ fois l'affixe de $\overrightarrow{u}$.

Milieu d'un segment : Si I est le milieu du segment [AB], alors l'affixe de I, $z_I$, est la moyenne des affixes de A et B :

$$z_I = \frac{z_A + z_B}{2}$$

Distance AB : La distance AB entre deux points A et B d'affixes $z_A$ et $z_B$ est donnée par le module de la différence de leurs affixes :

$$AB = |z_B - z_A| = |z_{\overrightarrow{AB}}|$$

3. Milieu, barycentre et alignement

Alignement de trois points : Trois points A, B et C d'affixes respectives $z_A$, $z_B$ et $z_C$ sont alignés si et seulement si le vecteur $\overrightarrow{AC}$ est colinéaire au vecteur $\overrightarrow{AB}$. Cela se traduit par le fait que le quotient $\frac{z_C - z_A}{z_B - z_A}$ est un nombre réel.

Parallélogramme : ABCD est un parallélogramme si et seulement si $\overrightarrow{AB} = \overrightarrow{DC}$, ce qui équivaut à $z_B - z_A = z_C - z_D$, et donc à :

$$z_D = z_A - z_B + z_C$$

Centre de gravité d'un triangle : Si G est le centre de gravité du triangle ABC, alors son affixe $z_G$ est la moyenne des affixes des sommets A, B et C :

$$z_G = \frac{z_A + z_B + z_C}{3}$$

C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !

Exercice 1

Dans le plan complexe, $\rm A$, $\rm B$ et $\rm C$ sont les points d'affixes : $z_{\rm A} = 5 + 3i$, $z_{\rm B} = 8 + i$ et $z_{\rm C} = 1 -3i$.
Déterminer l'affixe du point $\rm D$ tel que $\rm ABCD$ soit un parallélogramme.

Exercice 2

1. Lire les affixes $z_A$, $z_B$ et $z_C$ des points A,B et C.

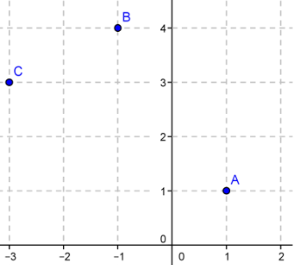
2. Déterminer l'affixe du vecteur $\overrightarrow {AB}$ graphiquement
    puis à l'aide des affixes.
3. Déterminer l'affixe de I milieu de [AC] graphiquement
    puis à l'aide des affixes.
4. Déterminer de deux façons différentes l'affixe du point D
    tel que ABCD soit un parallélogramme.

Correction de l'exercice 2 :

Question 1) Lecture graphique des affixes :

En observant le graphique, on peut lire les coordonnées des points A, B et C, et ainsi déterminer leurs affixes :

Point A : Coordonnées (2 ; 1). Donc, $z_A = 2 + i$.

Point B : Coordonnées (5 ; 2). Donc, $z_B = 5 + 2i$.

Point C : Coordonnées (3 ; -1). Donc, $z_C = 3 - i$.

Question 2) Affixe du vecteur $\overrightarrow{AB}$ graphiquement et par le calcul :

Graphiquement : Pour aller de A à B, on se déplace de 3 unités vers la droite (axe des réels) et de 1 unité vers le haut (axe des imaginaires). Donc, graphiquement, l'affixe de $\overrightarrow{AB}$ est $3 + i$.

Par le calcul : En utilisant la formule $z_{\overrightarrow{AB}} = z_B - z_A$, on obtient :

$$z_{\overrightarrow{AB}} = z_B - z_A = (5 + 2i) - (2 + i) = 5 + 2i - 2 - i = 3 + i$$

Les deux méthodes concordent.

Question 3) Affixe du milieu I de [AC] graphiquement et par le calcul :

Graphiquement : Le milieu I de [AC] semble avoir pour coordonnées (2.5 ; 0). Donc, graphiquement, l'affixe de I est $2.5 + 0i = 2.5 = \frac{5}{2}$.

Par le calcul : En utilisant la formule $z_I = \frac{z_A + z_C}{2}$, on obtient :

$$z_I = \frac{z_A + z_C}{2} = \frac{(2 + i) + (3 - i)}{2} = \frac{2 + i + 3 - i}{2} = \frac{5}{2} = 2.5$$

Les deux méthodes concordent.

Question 4) Affixe du point D tel que ABCD soit un parallélogramme (deux méthodes) :

Méthode 1 : Utilisation de l'égalité vectorielle $\overrightarrow{AB} = \overrightarrow{DC}$ :

Pour que ABCD soit un parallélogramme, il faut $\overrightarrow{AB} = \overrightarrow{DC}$. En termes d'affixes, cela donne $z_{\overrightarrow{AB}} = z_{\overrightarrow{DC}}$, soit $z_B - z_A = z_C - z_D$. On cherche $z_D$ :

$$z_D = z_C - (z_B - z_A) = z_C - z_B + z_A$$

En remplaçant par les affixes connues :

$$z_D = (3 - i) - (5 + 2i) + (2 + i) = 3 - i - 5 - 2i + 2 + i = (3 - 5 + 2) + (-i - 2i + i) = 0 - 2i = -2i$$

Donc $z_D = -2i$.

Méthode 2 : Utilisation des milieux des diagonales :

Dans un parallélogramme ABCD, les diagonales [AC] et [BD] ont le même milieu. On a déjà calculé l'affixe du milieu I de [AC] : $z_I = \frac{5}{2}$. Soit J le milieu de [BD]. Son affixe est $z_J = \frac{z_B + z_D}{2}$. On veut $I = J$, donc $z_I = z_J$ :

$$\frac{z_A + z_C}{2} = \frac{z_B + z_D}{2}$$

$$z_A + z_C = z_B + z_D$$

On isole $z_D$ :

$$z_D = z_A + z_C - z_B$$

On retrouve la même expression que dans la méthode 1, et donc $z_D = -2i$.

Conclusion : L'affixe du point D tel que ABCD soit un parallélogramme est $z_D = -2i$. Les coordonnées de D sont donc (0 ; -2).

Exercice 3

Soit A, B et C d'affixes respectives $z_A=-3+2i$ $z_B=1-2i$ $z_C=-1+6i$.
On considère le point M tel que $3\overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{AC}$.
1. Déterminer l'affixe $z_M$ du point M et en déduire ses coordonnées.
2. Faire une figure et placer les points A, B, C et M.
3. Soit D le symétrique de A par rapport à B. Déterminer l'affixe $z_D$ du point D.
4. Les points M, D et C sont-ils alignés? Justifier.

Correction de l'exercice 3 :

Question 1) Détermination de l'affixe $z_M$ :

On part de l'égalité vectorielle : $3\overrightarrow{MB}-\overrightarrow{MA}=\overrightarrow{AC}$.

Exprimons cette égalité en termes d'affixes :

$$3(z_B - z_M) - (z_A - z_M) = z_C - z_A$$

Développons et regroupons les termes pour isoler $z_M$ :

$$3z_B - 3z_M - z_A + z_M = z_C - z_A$$

$$3z_B - z_A - z_C + z_A = 3z_M - z_M$$

$$3z_B - z_C = 2z_M$$

$$z_M = \frac{3z_B - z_C}{2}$$

Substituons les affixes de A, B et C :

$$z_M = \frac{3(1 - 2i) - (-1 + 6i)}{2} = \frac{3 - 6i + 1 - 6i}{2} = \frac{4 - 12i}{2} = 2 - 6i$$

Donc, l'affixe de M est $z_M = 2 - 6i$. Les coordonnées de M sont (2 ; -6).

Question 2) Figure et placement des points :

Pour cette question, il faudrait construire un repère orthonormé et placer les points A, B, C et M en utilisant leurs coordonnées :

A(-3 ; 2), B(1 ; -2), C(-1 ; 6), M(2 ; -6).

(Description textuelle du placement - la figure nécessiterait une réalisation graphique).

Question 3) Affixe du point D symétrique de A par rapport à B :

Si D est le symétrique de A par rapport à B, alors B est le milieu de [AD]. En termes d'affixes, cela se traduit par :

$$z_B = \frac{z_A + z_D}{2}$$

On cherche $z_D$, donc on isole $z_D$ :

$$2z_B = z_A + z_D$$

$$z_D = 2z_B - z_A$$

Substituons les affixes de A et B :

$$z_D = 2(1 - 2i) - (-3 + 2i) = 2 - 4i + 3 - 2i = 5 - 6i$$

Donc, l'affixe de D est $z_D = 5 - 6i$.

Question 4) Alignement des points M, D et C :

Pour vérifier si les points M, D et C sont alignés, on peut regarder si les vecteurs $\overrightarrow{CM}$ et $\overrightarrow{CD}$ sont colinéaires. On calcule leurs affixes :

$$z_{\overrightarrow{CM}} = z_M - z_C = (2 - 6i) - (-1 + 6i) = 2 - 6i + 1 - 6i = 3 - 12i$$

$$z_{\overrightarrow{CD}} = z_D - z_C = (5 - 6i) - (-1 + 6i) = 5 - 6i + 1 - 6i = 6 - 12i$$

Pour vérifier la colinéarité, on peut regarder si le quotient $\frac{z_{\overrightarrow{CM}}}{z_{\overrightarrow{CD}}}$ est un nombre réel. Calculons ce quotient :

$$\frac{z_{\overrightarrow{CM}}}{z_{\overrightarrow{CD}}} = \frac{3 - 12i}{6 - 12i} = \frac{3(1 - 4i)}{6(1 - 2i)} = \frac{1 - 4i}{2(1 - 2i)} = \frac{1 - 4i}{2 - 4i}$$

Pour simplifier et voir si c'est réel, multiplions par le conjugué du dénominateur :

$$\frac{1 - 4i}{2 - 4i} \times \frac{2 + 4i}{2 + 4i} = \frac{(1 - 4i)(2 + 4i)}{(2 - 4i)(2 + 4i)} = \frac{2 + 4i - 8i - 16i^2}{2^2 - (4i)^2}$$

$$= \frac{2 - 4i + 16}{4 - 16i^2} = \frac{18 - 4i}{4 + 16} = \frac{18 - 4i}{20} = \frac{9}{10} - \frac{2}{10}i = \frac{9}{10} - \frac{1}{5}i$$

Le quotient $\frac{z_{\overrightarrow{CM}}}{z_{\overrightarrow{CD}}} = \frac{9}{10} - \frac{1}{5}i$ n'est pas un nombre réel (car la partie imaginaire $-\frac{1}{5}$ est non nulle).

Conclusion : Les vecteurs $\overrightarrow{CM}$ et $\overrightarrow{CD}$ ne sont pas colinéaires, donc les points M, D et C ne sont pas alignés.

Exercice 4

Soit A, B, C d'affixes respectives $z_A$, $z_B$ et $z_C$.
1. Soit I: le milieu du segment [AB]. On note $z_I$ l'affixe de I.
    a) Rappeler la définition vectorielle de I.
    b) En déduire $z_I$ en fonction de $z_A$ et $z_B$.
2. Soit G le centre de gravité du triangle A, B, C. On note $z_G$ l'affixe de G.
    On rappelle que G vérifie $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.
    Déterminer $z_G$ en fonction de $z_A$, $z_B$ et $z_C$.
3. On donne $z_A=3+2i$, $z_B=-2+5i$ et $z_C=-5-4i$.
    a) Déterminer l'affixe de J, milieu de [BC].
    b) Déterminer l'affixe de G, centre de gravité du triangle ABC.
    c) Les points J, G et A sont-ils alignés? Justifier.
    d) Cela était-il prévisible? Justifier.

Correction de l'exercice 4 :

Question 1) Milieu I de [AB] :

a) Définition vectorielle de I :

I est le milieu du segment [AB] si et seulement si $\overrightarrow{AI} = \overrightarrow{IB}$ ou encore $\overrightarrow{IA} + \overrightarrow{IB} = \overrightarrow{0}$.

b) Affixe $z_I$ en fonction de $z_A$ et $z_B$ :

En termes d'affixes, la relation $\overrightarrow{IA} + \overrightarrow{IB} = \overrightarrow{0}$ devient :

$$(z_A - z_I) + (z_B - z_I) = 0$$

$$z_A + z_B - 2z_I = 0$$

$$2z_I = z_A + z_B$$

$$z_I = \frac{z_A + z_B}{2}$$

Conclusion : L'affixe du milieu I de [AB] est la moyenne des affixes de A et B, soit $z_I = \frac{z_A + z_B}{2}$.

Question 2) Centre de gravité G du triangle ABC :

Détermination de $z_G$ en fonction de $z_A$, $z_B$ et $z_C$ :

On part de la relation vectorielle donnée : $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

En termes d'affixes, cette relation devient :

$$(z_A - z_G) + (z_B - z_G) + (z_C - z_G) = 0$$

$$z_A + z_B + z_C - 3z_G = 0$$

$$3z_G = z_A + z_B + z_C$$

$$z_G = \frac{z_A + z_B + z_C}{3}$$

Conclusion : L'affixe du centre de gravité G du triangle ABC est la moyenne des affixes des sommets, soit $z_G = \frac{z_A + z_B + z_C}{3}$.

Question 3) Applications numériques avec $z_A=3+2i$, $z_B=-2+5i$ et $z_C=-5-4i$ :

a) Affixe de J, milieu de [BC] :

En utilisant la formule du milieu avec $z_B$ et $z_C$ :

$$z_J = \frac{z_B + z_C}{2} = \frac{(-2 + 5i) + (-5 - 4i)}{2} = \frac{-2 + 5i - 5 - 4i}{2} = \frac{-7 + i}{2} = -\frac{7}{2} + \frac{1}{2}i$$

Donc, $z_J = -\frac{7}{2} + \frac{1}{2}i$.

b) Affixe de G, centre de gravité de ABC :

En utilisant la formule du centre de gravité avec $z_A$, $z_B$ et $z_C$ :

$$z_G = \frac{z_A + z_B + z_C}{3} = \frac{(3 + 2i) + (-2 + 5i) + (-5 - 4i)}{3} $$

$$= \frac{3 + 2i - 2 + 5i - 5 - 4i}{3} = \frac{(3 - 2 - 5) + (2i + 5i - 4i)}{3} = \frac{-4 + 3i}{3} = -\frac{4}{3} + i$$

Donc, $z_G = -\frac{4}{3} + i$.

c) Alignement des points J, G et A :

Pour vérifier l'alignement de J, G et A, on regarde si les vecteurs $\overrightarrow{AJ}$ et $\overrightarrow{AG}$ sont colinéaires. Calculons leurs affixes :

$$z_{\overrightarrow{AJ}} = z_J - z_A = (-\frac{7}{2} + \frac{1}{2}i) - (3 + 2i) = -\frac{7}{2} + \frac{1}{2}i - 3 - 2i = (-\frac{7}{2} - 3) + (\frac{1}{2}i - 2i) = -\frac{13}{2} - \frac{3}{2}i$$

$$z_{\overrightarrow{AG}} = z_G - z_A = (-\frac{4}{3} + i) - (3 + 2i) = -\frac{4}{3} + i - 3 - 2i = (-\frac{4}{3} - 3) + (i - 2i) = -\frac{13}{3} - i$$

Regardons le quotient $\frac{z_{\overrightarrow{AG}}}{z_{\overrightarrow{AJ}}}$ :

$$\frac{z_{\overrightarrow{AG}}}{z_{\overrightarrow{AJ}}} = \frac{-\frac{13}{3} - i}{-\frac{13}{2} - \frac{3}{2}i} = \frac{\frac{-13 - 3i}{3}}{\frac{-13 - 3i}{2}} = \frac{-13 - 3i}{3} \times \frac{2}{-13 - 3i} = \frac{2}{3}$$

Le quotient $\frac{z_{\overrightarrow{AG}}}{z_{\overrightarrow{AJ}}} = \frac{2}{3}$ est un nombre réel. Donc, les vecteurs $\overrightarrow{AJ}$ et $\overrightarrow{AG}$ sont colinéaires.

Conclusion : Les points J, G et A sont alignés.

d) Prévisibilité de l'alignement :

Oui, c'était prévisible. Dans un triangle, le centre de gravité G est situé à l'intersection des médianes. La médiane issue de A est la droite (AJ), où J est le milieu de [BC]. Puisque G est sur la médiane (AJ), les points A, G et J sont alignés par définition de la médiane et du centre de gravité.

Exercice 5

On rappelle que l'affixe du vecteur $\overrightarrow{OM}$ est égale à l'affixe du point M. Autrement dit $z_{\overrightarrow {OM}}=z_{M}$.
Soit A et B deux points d'affixes respectives $z_A$ et $z_B$.
1. Décomposer le vecteur $\overrightarrow{AB}$ en fonction des vecteurs $\overrightarrow{OA}$ et $\overrightarrow{OB}$.
2. En déduire l'affixe du vecteur $\overrightarrow{AB}$ en fonction de $z_A$ et $z_B$.

Correction de l'exercice 5 :

Cet exercice est une démonstration de cours importante, qui permet de comprendre comment calculer l'affixe d'un vecteur à partir des affixes des points.

Question 1) Décomposition vectorielle de $\overrightarrow{AB}$ :

On souhaite exprimer le vecteur $\overrightarrow{AB}$ en fonction des vecteurs $\overrightarrow{OA}$ et $\overrightarrow{OB}$. On peut utiliser la relation de Chasles, en introduisant le point O :

$$\overrightarrow{OA} + \overrightarrow{AB} = \overrightarrow{OB}$$

Pour isoler $\overrightarrow{AB}$, on soustrait $\overrightarrow{OA}$ de chaque côté :

$$\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$$

Conclusion : La décomposition vectorielle de $\overrightarrow{AB}$ en fonction de $\overrightarrow{OA}$ et $\overrightarrow{OB}$ est $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$.

Question 2) Affixe du vecteur $\overrightarrow{AB}$ en fonction de $z_A$ et $z_B$ :

On sait que l'affixe du vecteur $\overrightarrow{OM}$ est égale à l'affixe du point M, c'est-à-dire $z_{\overrightarrow{OM}} = z_M$. Appliquons cette propriété aux vecteurs $\overrightarrow{OA}$ et $\overrightarrow{OB}$ :

$$z_{\overrightarrow{OA}} = z_A \quad \text{et} \quad z_{\overrightarrow{OB}} = z_B$$

De plus, l'affixe d'une somme de vecteurs est la somme des affixes, et l'affixe d'une différence de vecteurs est la différence des affixes. Donc, l'affixe de $\overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA}$ est :

$$z_{\overrightarrow{AB}} = z_{\overrightarrow{OB}} - z_{\overrightarrow{OA}} = z_B - z_A$$

Conclusion : L'affixe du vecteur $\overrightarrow{AB}$ est donnée par $z_{\overrightarrow{AB}} = z_B - z_A$. C'est une formule fondamentale à connaître et à savoir redémontrer.

Exercice 6

Dans le plan complexe, déterminer et construire l'ensemble des points M d'affixe $z$ tels que $2z\overline{z}=3(z+\overline{z})$

Correction de l'exercice 6 :

On cherche à déterminer l'ensemble des points M d'affixe $z$ vérifiant l'équation $2z\overline{z}=3(z+\overline{z})$.

Pour résoudre ce type de problème, on pose $z = x + iy$, où $x$ et $y$ sont des nombres réels. On sait que $\overline{z} = x - iy$, et que :

$$z\overline{z} = |z|^2 = x^2 + y^2$$

$$z + \overline{z} = (x + iy) + (x - iy) = 2x$$

Substituons ces expressions dans l'équation donnée :

$$2(x^2 + y^2) = 3(2x)$$

$$2x^2 + 2y^2 = 6x$$

Divisons par 2 :

$$x^2 + y^2 = 3x$$

Pour reconnaître l'ensemble géométrique, on réarrange l'équation pour faire apparaître la forme canonique d'un cercle. On regroupe les termes en $x$ et on complète le carré :

$$x^2 - 3x + y^2 = 0$$

Pour compléter le carré en $x$, on prend la moitié du coefficient de $x$ (qui est $-3$), soit $-\frac{3}{2}$, et on ajoute et soustrait son carré $(-\frac{3}{2})^2 = \frac{9}{4}$ :

$$\left(x^2 - 3x + \frac{9}{4}\right) - \frac{9}{4} + y^2 = 0$$

$$\left(x - \frac{3}{2}\right)^2 + y^2 = \frac{9}{4}$$

Cette équation est de la forme $(x - a)^2 + (y - b)^2 = R^2$, qui est l'équation d'un cercle de centre $\Omega(a ; b)$ et de rayon $R$. Ici, on a :

Centre $\Omega$ : $\left(\frac{3}{2} ; 0\right)$ (affixe $z_\Omega = \frac{3}{2}$)

Rayon $R$ : $\sqrt{\frac{9}{4}} = \frac{3}{2}$

Conclusion : L'ensemble des points M d'affixe $z$ tels que $2z\overline{z}=3(z+\overline{z})$ est le cercle de centre $\Omega$ d'affixe $\frac{3}{2}$ et de rayon $\frac{3}{2}$.

Construction : Pour construire ce cercle, on place le centre $\Omega$ de coordonnées $(\frac{3}{2} ; 0)$ sur l'axe des réels. Le cercle passe par l'origine O car la distance de $\Omega$ à l'origine est égale au rayon $\frac{3}{2}$. Il passe également par le point d'affixe 3, qui est diamétralement opposé à l'origine par rapport à $\Omega$.

Exercice 7

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
À tout point $M$ d'affixe $z$, on associe le point $M'$ d'affixe $z'=z^2+4z+3$.
Déterminer l'ensemble E des points $M$ d'affixe $z = x +iy$ où $x$ et $y$ sont réels,
tels que le point $M'$ soit sur l'axe des réels. Puis représenter l'ensemble E.

Correction de l'exercice 7 :

On cherche l'ensemble des points M d'affixe $z = x + iy$ tels que $M'$ d'affixe $z' = z^2 + 4z + 3$ soit sur l'axe des réels. Pour que $M'$ soit sur l'axe des réels, il faut et il suffit que la partie imaginaire de $z'$ soit nulle, c'est-à-dire $\rm Im(z') = 0$.

Calculons $z'$ en fonction de $x$ et $y$. On a $z = x + iy$, donc :

$$z' = (x + iy)^2 + 4(x + iy) + 3$$

Développons :

$$z' = (x^2 + 2ixy + (iy)^2) + 4x + 4iy + 3$$

$$z' = x^2 + 2ixy - y^2 + 4x + 4iy + 3$$

Regroupons les parties réelle et imaginaire :

$$z' = (x^2 - y^2 + 4x + 3) + i(2xy + 4y)$$

La partie imaginaire de $z'$ est $\rm Im(z') = 2xy + 4y$. On veut que $\rm Im(z') = 0$, donc :

$$2xy + 4y = 0$$

Factorisons par $2y$ :

$$2y(x + 2) = 0$$

Pour qu'un produit de facteurs soit nul, il faut et il suffit qu'au moins l'un des facteurs soit nul. Donc, on a deux possibilités :

Cas 1 : $2y = 0$, ce qui implique $y = 0$. Dans ce cas, les points M ont une affixe réelle $z = x$, et sont donc sur l'axe des réels.

Cas 2 : $x + 2 = 0$, ce qui implique $x = -2$. Dans ce cas, les points M ont une affixe de la forme $z = -2 + iy$, et sont donc sur la droite verticale d'équation $x = -2$.

Conclusion : L'ensemble E des points M tels que $M'$ soit sur l'axe des réels est la réunion de deux ensembles :

L'axe des réels (axe des abscisses, d'équation $y = 0$).

La droite verticale d'équation $x = -2$.

Représentation graphique :

L'ensemble E est constitué de l'axe des réels et de la droite verticale passant par le point d'affixe -2. Ce sont deux droites perpendiculaires qui se coupent au point de coordonnées (-2 ; 0), d'affixe -2.

Exercice 8

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
Soit $z$ un nombre complexe différent de $i$.
On note $z'=\frac{z+i}{z-i}$. On appelle X et Y respectivement la partie réelle et imaginaire de $z'$.
1. On pose $z=x+iy$ où $x$ et $y$ sont réels. Déterminer X et Y en fonction de $x$ et $y$.
2. Déterminer l'ensemble $\mathscr E_1$ des points M d'affixe $z$ tels que $z'$ est réel.
3. Déterminer l'ensemble $\mathscr E_2$ des points M d'affixe $z$ tels que $z'$ est imaginaire pur.

Correction de l'exercice 8 :

On considère la transformation $z'=\frac{z+i}{z-i}$, avec $z \neq i$. On pose $z = x + iy$ et $z' = X + iY$, où $x, y, X, Y$ sont réels.

Question 1) Détermination de X et Y en fonction de $x$ et $y$ :

Substituons $z = x + iy$ dans l'expression de $z'$ :

$$z' = \frac{(x + iy) + i}{(x + iy) - i} = \frac{x + i(y + 1)}{x + i(y - 1)}$$

Pour obtenir la forme algébrique de $z'$, on multiplie le numérateur et le dénominateur par le conjugué du dénominateur, qui est $x - i(y - 1) = x - i(y - 1)$ :

$$z' = \frac{[x + i(y + 1)][x - i(y - 1)]}{[x + i(y - 1)][x - i(y - 1)]} = \frac{x^2 - ix(y - 1) + ix(y + 1) - i^2(y + 1)(y - 1)}{x^2 - [i(y - 1)]^2}$$

$$z' = \frac{x^2 - ixy + ix + ixy + iy + (y^2 - 1)}{x^2 + (y - 1)^2} = \frac{(x^2 + y^2 - 1) + i(x + y)}{x^2 + (y - 1)^2}$$

Donc, $z' = X + iY$ avec :

$$X = \frac{x^2 + y^2 - 1}{x^2 + (y - 1)^2} \quad \text{et} \quad Y = \frac{x + y}{x^2 + (y - 1)^2}$$

Conclusion : $X = \frac{x^2 + y^2 - 1}{x^2 + (y - 1)^2}$ et $Y = \frac{x + y}{x^2 + (y - 1)^2}$.

Question 2) Ensemble $\mathscr E_1$ pour $z'$ réel :

Pour que $z'$ soit réel, il faut et il suffit que sa partie imaginaire soit nulle, soit $Y = 0$. Donc :

$$\frac{x + y}{x^2 + (y - 1)^2} = 0$$

Une fraction est nulle si et seulement si son numérateur est nul (et le dénominateur non nul, ce qui est le cas car $z \neq i$ donc $y \neq 1$ ou $x \neq 0$ si $y=1$). Donc, on doit avoir :

$$x + y = 0 \Leftrightarrow y = -x$$

L'ensemble $\mathscr E_1$ est donc l'ensemble des points M d'affixe $z = x + iy$ tels que $y = -x$. C'est la droite d'équation $y = -x$, qui est la deuxième bissectrice (droite passant par l'origine et de pente -1).

Conclusion : $\mathscr E_1$ est la droite d'équation $y = -x$.

Question 3) Ensemble $\mathscr E_2$ pour $z'$ imaginaire pur :

Pour que $z'$ soit imaginaire pur, il faut et il suffit que sa partie réelle soit nulle, soit $X = 0$. Donc :

$$\frac{x^2 + y^2 - 1}{x^2 + (y - 1)^2} = 0$$

De même, le numérateur doit être nul (et le dénominateur non nul) :

$$x^2 + y^2 - 1 = 0 \Leftrightarrow x^2 + y^2 = 1$$

L'ensemble $\mathscr E_2$ est donc l'ensemble des points M d'affixe $z = x + iy$ tels que $x^2 + y^2 = 1$. C'est le cercle de centre O (l'origine) et de rayon 1 (le cercle unité).

Il faut vérifier que le dénominateur $x^2 + (y - 1)^2$ n'est jamais nul pour les points du cercle unité. Si $x^2 + y^2 = 1$, alors $x^2 + (y - 1)^2 = x^2 + y^2 - 2y + 1 = 1 - 2y + 1 = 2 - 2y = 2(1 - y)$. Ce dénominateur est nul si $y = 1$. Mais si $y = 1$ et $x^2 + y^2 = 1$, alors $x^2 + 1^2 = 1$, donc $x^2 = 0$, donc $x = 0$. Le seul point pour lequel le dénominateur pourrait être nul est le point d'affixe $i$ (correspondant à $z = i$), mais ce point est exclu de l'ensemble de définition de $z'$. Donc, pour tous les points du cercle unité, le dénominateur est non nul.

Conclusion : $\mathscr E_2$ est le cercle de centre O et de rayon 1, privé du point d'affixe $i$ (mais en fait le point d'affixe $i$ est déjà exclu du domaine de définition de $z'$, donc on peut dire que $\mathscr E_2$ est le cercle de centre O et de rayon 1).

Exercice 9

Le plan complexe est muni d'un repère orthonormé direct $(O; \overrightarrow{u} ; \overrightarrow{v} )$.
À tout point $M$ d'affixe $z$ différente de $3i$, on associe le point $M'$ d'affixe $z'=\frac{z-2}{iz+3}$.
On appelle X et Y respectivement la partie réelle et imaginaire de $z'$.
1. On pose $z=x+iy$ où $x$ et $y$ sont réels. Déterminer X et Y en fonction de $x$ et $y$.
2. Déterminer l'ensemble $\mathscr E_1$ des points M d'affixe $z$ tels que $z'$ soit réel.
3. Déterminer l'ensemble $\mathscr E_2$ des points M d'affixe $z$ tels que $z'$ soit imaginaire pur.

Correction de l'exercice 9 :

On considère la transformation $z'=\frac{z-2}{iz+3}$, définie pour $z \neq 3i$. On pose $z = x + iy$ et $z' = X + iY$, où $x, y, X, Y$ sont réels.

Question 1) Détermination de X et Y en fonction de $x$ et $y$ :

Substituons $z = x + iy$ dans l'expression de $z'$ :

$$z' = \frac{(x + iy) - 2}{i(x + iy) + 3} = \frac{(x - 2) + iy}{3 + ix + i^2y} = \frac{(x - 2) + iy}{(3 - y) + ix}$$

Pour obtenir la forme algébrique de $z'$, on multiplie le numérateur et le dénominateur par le conjugué du dénominateur, qui est $(3 - y) - ix$ :

$$z' = \frac{[(x - 2) + iy][(3 - y) - ix]}{[(3 - y) + ix][(3 - y) - ix]} = \frac{(x - 2)(3 - y) - ix(x - 2) + iy(3 - y) - i^2xy}{(3 - y)^2 - (ix)^2}$$

$$z' = \frac{(3x - xy - 6 + 2y) - ix^2 + 2ix + i3y - iy^2 + xy}{(3 - y)^2 + x^2}$$

Regroupons les parties réelle et imaginaire :

$$z' = \frac{(3x - xy - 6 + 2y + xy) + i(-x^2 + 2x + 3y - y^2)}{(3 - y)^2 + x^2} = \frac{(3x + 2y - 6) + i(-x^2 - y^2 + 2x + 3y)}{(3 - y)^2 + x^2}$$

Donc, $z' = X + iY$ avec :

$$X = \frac{3x + 2y - 6}{(3 - y)^2 + x^2} \quad \text{et} \quad Y = \frac{-x^2 - y^2 + 2x + 3y}{(3 - y)^2 + x^2}$$

Conclusion : $X = \frac{3x + 2y - 6}{x^2 + (3 - y)^2}$ et $Y = \frac{-x^2 - y^2 + 2x + 3y}{x^2 + (3 - y)^2}$.

Question 2) Ensemble $\mathscr E_1$ pour $z'$ réel :

Pour que $z'$ soit réel, il faut et il suffit que sa partie imaginaire soit nulle, soit $Y = 0$. Donc :

$$\frac{-x^2 - y^2 + 2x + 3y}{(3 - y)^2 + x^2} = 0$$

Le numérateur doit être nul (et le dénominateur non nul, ce qui est vrai car $z \neq 3i$ implique $y \neq 3$ ou $x \neq 0$ si $y=3$). Donc, on doit avoir :

$$-x^2 - y^2 + 2x + 3y = 0$$

$$x^2 - 2x + y^2 - 3y = 0$$

Complétons les carrés pour $x$ et $y$ :

$$(x^2 - 2x + 1) - 1 + (y^2 - 3y + \frac{9}{4}) - \frac{9}{4} = 0$$

$$(x - 1)^2 + \left(y - \frac{3}{2}\right)^2 = 1 + \frac{9}{4} = \frac{13}{4}$$

C'est l'équation d'un cercle de centre $\Omega(1 ; \frac{3}{2})$ et de rayon $R = \sqrt{\frac{13}{4}} = \frac{\sqrt{13}}{2}$.

Conclusion : $\mathscr E_1$ est le cercle de centre $\Omega$ d'affixe $1 + \frac{3}{2}i$ et de rayon $\frac{\sqrt{13}}{2}$.

Question 3) Ensemble $\mathscr E_2$ pour $z'$ imaginaire pur :

Pour que $z'$ soit imaginaire pur, il faut et il suffit que sa partie réelle soit nulle, soit $X = 0$. Donc :

$$\frac{3x + 2y - 6}{(3 - y)^2 + x^2} = 0$$

Le numérateur doit être nul :

$$3x + 2y - 6 = 0$$

C'est l'équation d'une droite. On peut l'écrire sous la forme $y = -\frac{3}{2}x + 3$.

Conclusion : $\mathscr E_2$ est la droite d'équation $3x + 2y - 6 = 0$, ou $y = -\frac{3}{2}x + 3$.

Exercice 10

On considère la suite de nombres complexes $(z_n)$ définie par $z_0=100$ et pour tout entier naturel $n$, $z_{n+1}=\frac i3 z_n$.
Le plan est muni d'un repère orthonormé direct (O;$\vec u$;$\vec v$).
Pour tout entier naturel $n$, on note ${\rm M}_n$ le point d'affixe $z_n$.
Démontrer que pour tout entier naturel $n$, les points ${\rm O}$, ${\rm M}_n$ et ${\rm M}_{n+2}$ sont alignés.

Correction de l'exercice 10 :

On veut démontrer que pour tout entier naturel $n$, les points O, ${\rm M}_n$ et ${\rm M}_{n+2}$ sont alignés. Pour cela, il faut montrer que les vecteurs $\overrightarrow{OM_n}$ et $\overrightarrow{OM_{n+2}}$ sont colinéaires. En termes d'affixes, cela signifie que le quotient $\frac{z_{n+2} - z_O}{z_n - z_O}$ est un nombre réel. Comme $z_O = 0$, on doit montrer que $\frac{z_{n+2}}{z_n}$ est un nombre réel.

On a la relation de récurrence $z_{n+1} = \frac{i}{3} z_n$. Calculons $z_{n+2}$ en fonction de $z_n$ :

$$z_{n+2} = \frac{i}{3} z_{n+1}$$

Substituons l'expression de $z_{n+1}$ en fonction de $z_n$ :

$$z_{n+2} = \frac{i}{3} \left(\frac{i}{3} z_n\right) = \left(\frac{i}{3} \times \frac{i}{3}\right) z_n = \frac{i^2}{3^2} z_n = \frac{-1}{9} z_n$$

Donc, on a la relation $z_{n+2} = -\frac{1}{9} z_n$. Calculons le quotient $\frac{z_{n+2}}{z_n}$ :

$$\frac{z_{n+2}}{z_n} = \frac{-\frac{1}{9} z_n}{z_n} = -\frac{1}{9}$$

Le quotient $\frac{z_{n+2}}{z_n} = -\frac{1}{9}$ est un nombre réel (c'est un nombre réel sans partie imaginaire).

Conclusion : Puisque $\frac{z_{n+2}}{z_n} = \frac{z_{n+2} - 0}{z_n - 0} = \frac{z_{n+2} - z_O}{z_n - z_O} = \frac{z_{\overrightarrow{OM_{n+2}}}}{z_{\overrightarrow{OM_n}}}$ est un nombre réel, les vecteurs $\overrightarrow{OM_n}$ et $\overrightarrow{OM_{n+2}}$ sont colinéaires. Par conséquent, les points O, ${\rm M}_n$ et ${\rm M}_{n+2}$ sont alignés pour tout entier naturel $n$.

Interprétation géométrique : La relation $z_{n+2} = -\frac{1}{9} z_n$ signifie que le point ${\rm M}_{n+2}$ est l'image du point ${\rm M}_n$ par l'homothétie de centre O et de rapport $-\frac{1}{9}$. Une homothétie de centre O transforme une droite passant par O en elle-même. Donc, la droite $(O{\rm M}_n)$ est transformée en la droite $(O{\rm M}_{n+2})$. Comme O est invariant par l'homothétie, et que ${\rm M}_n$ est transformé en ${\rm M}_{n+2}$, les points O, ${\rm M}_n$ et ${\rm M}_{n+2}$ sont alignés.

Exercices : Nombres Complexes et Géométrie

Nombres Complexes et Géométrie