Génération d'une suite, variation et représentation graphique
Consolidez votre compréhension sur la génération des suites numériques, leur variation et représentation graphique à travers ces exercices ciblés.
Petit rappel des points clés sur la génération des suites, leur variation et représentation graphique. C'est toujours bon de revoir les bases avant de se lancer dans les exercices !
1. Génération d'une suite
Une suite numérique peut être définie de deux manières principales :
a. Formule explicite : Chaque terme $u_n$ est directement calculé en fonction de $n$. Par exemple, $u_n = 2n + 3$.
b. Relation de récurrence : Chaque terme $u_{n+1}$ est défini en fonction du terme précédent $u_n$ (et parfois des termes antérieurs). Par exemple, $u_{n+1} = u_n + 5$, avec un premier terme $u_0$ donné.
2. Variation d'une suite
Le sens de variation d'une suite décrit comment les termes évoluent :
a. Croissante : Si $u_{n+1} \geqslant u_n$ pour tout $n$. Les termes augmentent ou restent constants.
b. Décroissante : Si $u_{n+1} \leqslant u_n$ pour tout $n$. Les termes diminuent ou restent constants.
c. Constante : Si $u_{n+1} = u_n$ pour tout $n$. Les termes restent inchangés.
Pour déterminer la variation, on étudie souvent le signe de la différence $u_{n+1} - u_n$.
3. Représentation graphique
Graphiquement, une suite $(u_n)$ est représentée par un ensemble de points de coordonnées $(n, u_n)$. L'axe des abscisses représente les rangs $n$, et l'axe des ordonnées les valeurs $u_n$. On obtient un nuage de points discrets.
Observer la représentation graphique aide à visualiser le sens de variation de la suite.
Rappels en tête ? Alors, échauffez-vous avec les exercices suivants !
Calcul des termes d'une suite
Exercice 1
Soit la suite $(u_n)$ définie pour tout entier naturel $n$, par $u_n=3n^2-1$. Calculer les cinq premiers termes de la suite $(u_n)$.
Exercice 2
Soit la suite $(u_n)$ définie pour tout entier naturel $n$, par $u_n=-5n^2+2$. Calculer les cinq premiers termes de la suite $(u_n)$.
Exercice 3
- Soit la suite $(u_n)$ définie, pour tout entier naturel $n$, par : $\begin{cases} u_0=6 \\ u_{n+1}=2u_n-5 \end{cases}$ Déterminer ses quatre premiers termes.
- Soit la suite $(v_n)$ définie par $v_n=5+2^n$. Calculer ses quatre premiers termes.
- Que constate-t-on ?
- À l'aide de la calculatrice, retrouver les résultats des questions 1. et 2.
Exercice 4
- Soit la suite $(u_n)$ définie, pour tout entier naturel $n$, par : $\begin{cases} u_0=7 \\ u_{n+1}=u_n+2n+5 \end{cases}$ Déterminer ses quatre premiers termes.
- Soit la suite $(v_n)$ définie par $v_n=n^2+4n+7$. Calculer ses quatre premiers termes.
- Que constate-t-on ?
- À l'aide de la calculatrice, retrouver les résultats des questions 1. et 2.
Exercice 5
Une association caritative a constaté que chaque année 20 \% des donateurs de l'année précédente ne renouvelaient pas leur don mais que 300 nouveaux donateurs en effectuaient un. On étudie le nombre de donateurs au fil des années. Lors de la 1ère année de l'étude en l'an 2020, l'association comptait 1 000 donateurs. On note $u_n$ le nombre de donateurs l'année $2 020 + n$. On a donc $u_0=1000$.
- Justifier que diminuer de 20 % revient à multiplier par 0,8.
- Calculer $u_1$, le nombre de donateurs en 2021. Puis calculer $u_2$ et $u_3$. Que représentent ces valeurs ?
Exercice 6
Le 1er janvier 2020, Ahmed place 1 000 € sur un compte rémunéré à 4\% d'intérêts composés annuels. Chaque 1er janvier à partir de 2021, il dépose 100 € supplémentaires sur le livret. On note $C_0$ le capital de départ en euros, donc $C_0=1000$, puis pour tout entier naturel $n$, $C_n$ est le capital l'année $2020+n$.
- Calculer le capital $C_1$ disponible au 1er janvier 2021, puis le capital $C_2$.
- À l'aide de la calculatrice, déterminer le capital disponible le 1er janvier 2035.
Représentation graphique et sens de variation
Exercice 7
Complétez le tableau de valeurs suivant puis placez les points dans le repère ci-contre.
| $n$ | $u_n$ |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
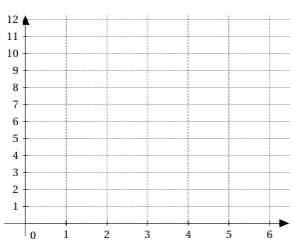
Exercice 8
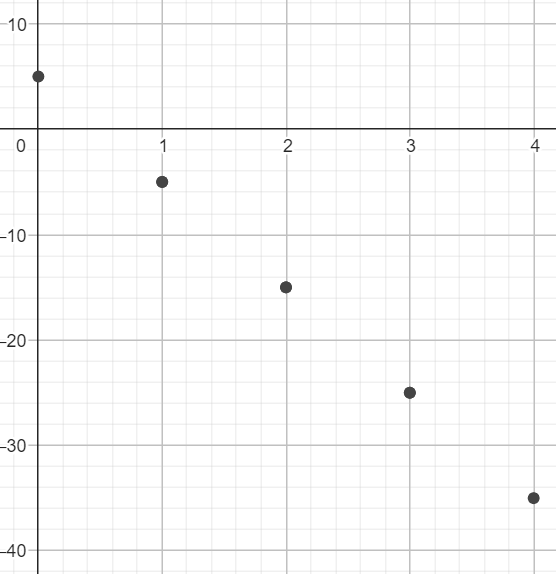
On considère la suite définie par son terme initial $u_0=5$ et par la formule de récurrence, pour tout entier naturel $n$, $ u_{n+1}=-10+u_n$. Représenter la suite $(u_n)$ puis étudiez les variations de $(u_n)$.
Exercice 9
Déterminer le sens de variation de la suite $(u_n)$ en calculant la différence $u_{n+1}-u_n$ dans les cas suivants :
- $u_0= 9$ et $u_{n+1} = u_n-n^2$.
- $u_0=-7$ et $u_{n+1} = u_n-7n$.
- $u_0=-1$ et $u_{n+1} = u_n+n^2+3$.
Exercice 10
Pour chacune des suites, exprimer $u_{n+1}$ en fonction de $n$, puis déterminer le sens de variation de la suite en étudiant le signe de $u_{n+1}-u_n$.
- $u_n = 3n^2-4$
- $u_n = 5n-8 $
- $u_n = n^2-2n+1 $
Avec l'outil informatique
Exercice 11
- Calculez sur tableur les termes de rangs 0, 1 et 19 de la suite $(u_n)$ définie par l'expression de son terme de rang $n$: pour tout entier naturel $n$, $u_n=2n-1$.
- Calculez sur tableur les termes de rangs 1, 2 et 39 de la suite $(v_n)$ définie par récurrence: terme initial $v_0=1,1$ et, pour tout entier naturel $n$, $v_{n+1}=2v_n-1$.
Exercice 12
On considère la suite $(u_n)$ définie par son premier terme $u_0$ et la relation de récurrence $u_{n+1}=4u_n-1$ pour tout entier naturel $n$. Écrire un algorithme de calcul de $N$-ième terme de la suite $(u_n)$ à partir de la saisie du premier terme et de l'entier $N$.