Fonctions Polynômes de Degré 2
Ici, vous trouverez une série d'exercices pour vous entraîner sur les fonctions polynômes de degré 2, un outil essentiel en mathématiques et dans de nombreux domaines techniques (STMG STI2D).
Revoyons ensemble les points essentiels sur les fonctions polynômes de degré 2 avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir en STMG et STI2D !
1. Représentations graphiques des fonctions de référence
Nous allons revoir les représentations graphiques de trois formes simples de fonctions polynômes de degré 2 :
Forme 𝑥 ↦ 𝑎𝑥² :
Ces fonctions ont une parabole comme représentation graphique, avec le sommet à l'origine (0 ; 0) et l'axe de symétrie est l'axe des ordonnées (y). Le coefficient $a$ détermine l'allure :
- Si $a > 0$, la parabole est ouverte vers le haut (en "U").
- Si $a < 0$, la parabole est ouverte vers le bas (en "U inversé").
- Plus $|a|$ est grand, plus la parabole est "étroite".
Forme 𝑥 ↦ 𝑎𝑥² + 𝑐 :
Ces fonctions sont des translations verticales des fonctions $x \mapsto ax^2$. Le sommet est en (0 ; c) et l'axe de symétrie reste l'axe des ordonnées.
Forme 𝑥 ↦ 𝑎(𝑥 − 𝑥₁)(𝑥 − 𝑥₂) :
Cette forme factorisée nous donne directement les racines $x_1$ et $x_2$ de la fonction (les valeurs de $x$ pour lesquelles $f(x)=0$). La parabole coupe l'axe des abscisses aux points d'abscisses $x_1$ et $x_2$. L'axe de symétrie se trouve au milieu des racines, à l'abscisse $\dfrac{x_1 + x_2}{2}$.
2. Éléments caractéristiques de la forme factorisée 𝑥 ↦ 𝑎(𝑥 − 𝑥₁)(𝑥 − 𝑥₂)
Considérons une fonction polynôme de degré 2 sous forme factorisée : $f(x) = a(x - x_1)(x - x_2)$.
Signe de la fonction : Le signe de $f(x)$ dépend du signe de $a$ et de la position par rapport aux racines $x_1$ et $x_2$ (en supposant $x_2 < x_1$).
Si $a > 0$ et $a < 0$ :
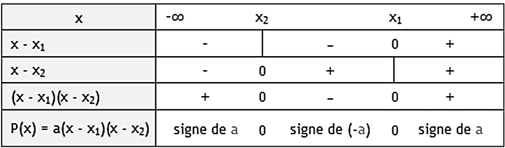
Extremum : L'extremum (minimum si $a>0$, maximum si $a<0$) est atteint à l'abscisse du sommet, qui est le milieu des racines : $\alpha = \dfrac{x_1 + x_2}{2}$. L'extremum est alors $f(\alpha)$.
Allure de la courbe : Déjà vu, dépend du signe de $a$ (ouverte vers le haut si $a>0$, vers le bas si $a<0$).
Axe de symétrie : La droite verticale d'équation $x = \alpha = \dfrac{x_1 + x_2}{2}$ est l'axe de symétrie de la parabole.
Rappels essentiels mémorisés ? 💪 À vous de jouer avec les exercices !
Exercice 1
Donner le sens de variation de chacune des fonctions définies sur $\mathbb{R}$ :
1. $f(x)=7x^2$
2. $g(x)=-5x^2$
3. $h(x)=0.28x^2$
Exercice 2
Soit $h$ une fonction définie sur $\mathbb{R}$ par $h(x)=ax^2$. Déterminer la valeur de $a$ sachant que $h(2)=6$.
Exercice 3
Déterminer l'expression de la fonction polynôme de degré 2 définie su $\mathbb{R}$ dont la représentation graphique figure ci dessous :

Exercice 4
Ci-contre, on donne le tableau de valeur d'une fonction du type $x \mapsto ax^2$. Déterminer la valeur de $a$.
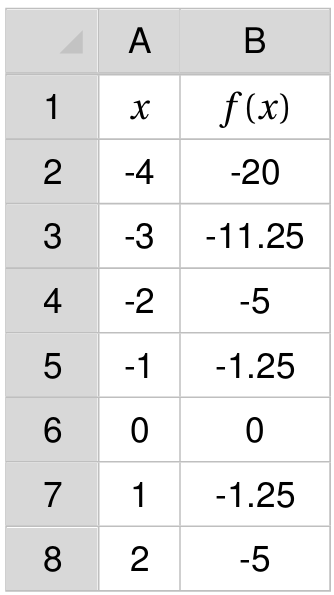
Exercice 5
Donner le sens de variation de chacune des fonctions définies sur $\mathbb{R}$ :
1. $f(x)=-2x^2+3$
2. $g(x)=-5x^2-3$
3. $h(x)=0.28x^2+2$
Exercice 6
Soit $f$ une fonction définie sur $\mathbb{R}$ par $f(t)=at^2+b$. Déterminer la valeur de $a$ sachant que $f(-1)=-2$et $f(2)=3$.
Exercice 7
Déterminer l'expression de la fonction polynôme de degré 2 définie su $\mathbb{R}$ dont la représentation graphique figure ci dessous :
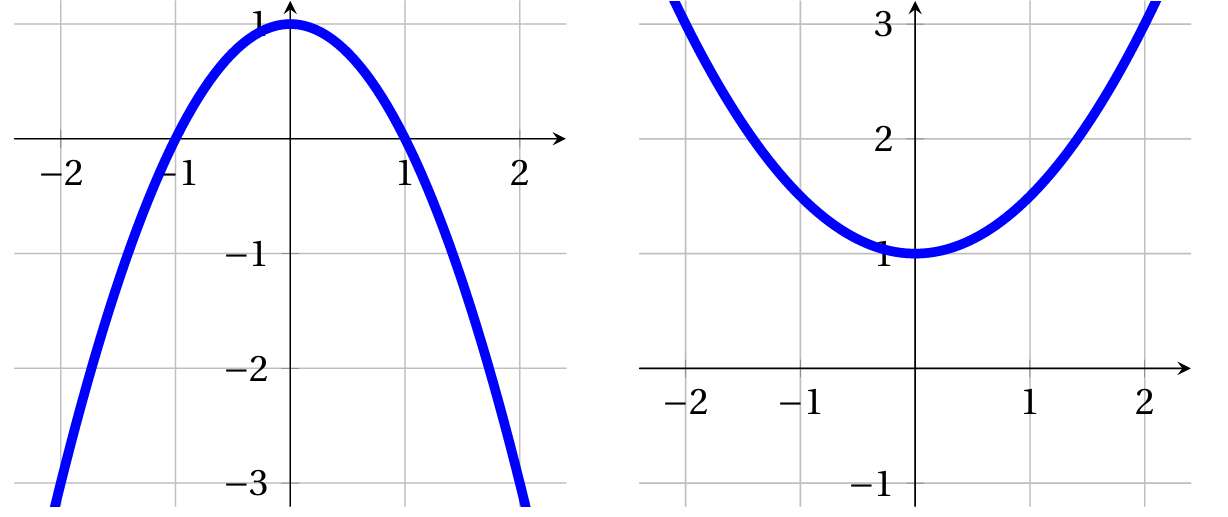
Exercice 8
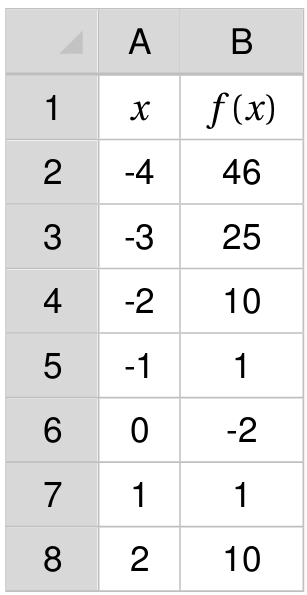
Ci-contre, on donne le tableau de valeur d'une fonction du type $x \mapsto ax^2+b$. Déterminer la valeur de $a$ et de $b$.
Exercice 9
Soit $f$ une fonction qui est définie sur $\mathbb{R}$ par $f(x)=-3.6x^2$ et le vecteur $\vec{u}$ de coordonnées $\begin{pmatrix} 0 \\ 4 \end{pmatrix}$. Donner l'expression de la fonction $g$ dont on obtient la représentation graphique par la translation de vecteur $\vec{u}$ appliquée à la courbe représentative de la fonction $f$.
Exercice 10
Donner les racines de chacune des fonctions définies sur $\mathbb{R}$ :
1. $f(x)=-2(x-3)(x-8)$
2. $g(x)=-5(x+5)(x-2,65)$
3. $h(x)=0.28(x+8,72)(x+7)$
Exercice 11
Déterminer l'expression de la fonction polynôme de degré $2$, sachant qu'elle admet une seule racine : $-2$ et que $g(2)=8$.
Exercice 12
Déterminer le signe de la fonction polynôme de degré 2 définie sur $\mathbb{R}$.
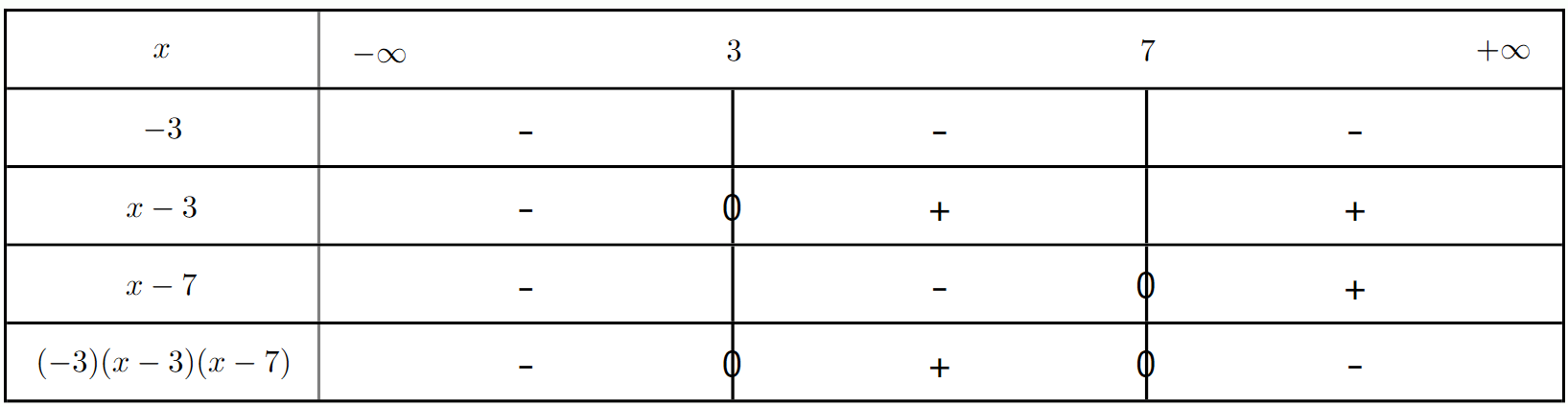
1. $f(x)=-3(x-5)(x-7)$
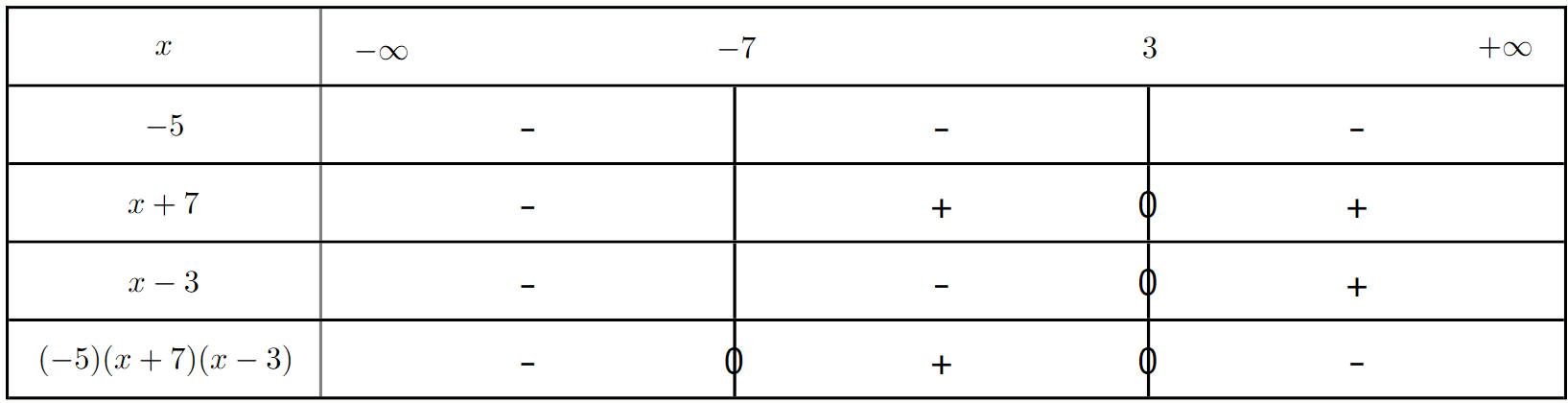
2. $g(x)=-5(x+7)(x-3)$
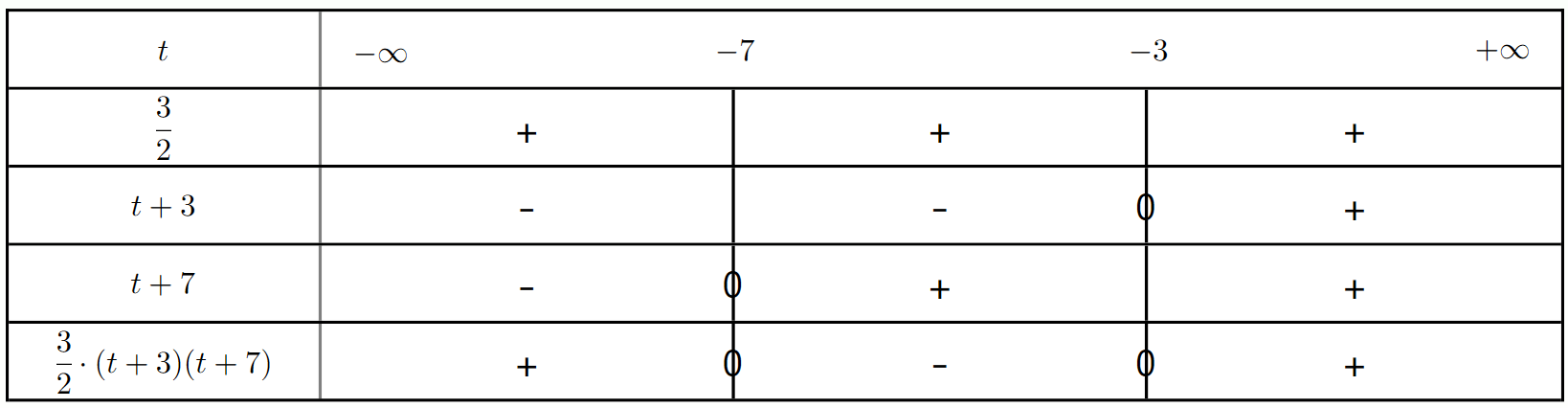
3. $h(t)=1,5(t+3)(t+7)$
Exercice 13
L'indice de masse corporelle d'une personne (IMC) se calcule grâce à la formule suivante : $IMC = \dfrac{\text{Masse}}{\text{Taille}^2}$ (masse en kg, taille en m). Une personne commence à être en surpoids si son IMC est supérieur ou égal à 25.
1. Déterminer l'IMC d'une personne mesurant $1,84$m et pesant $65$kg.
2. Quelle est la taille d'une personne d'IMC égal à $23,5$ et pesant $64$kg ?
3. Quel est le poids d'une personne d'IMC égal à $18$ et mesurant $1,73$m ?
4. Combien pèse une personne en surpoids mesurant $1,71$m ?
Conformément à l'usage de la langue courante, on utilise le mot « poids » pour désigner ce qui est en fait la masse.
Exercice 14
On étudie l'évolution, en fonction du temps, d'une population de levures présentes dans un milieu liquide. Au bout de $300$min, le nombre de levures est stationnaire pendant $30$min, puis il peut être modélisé par la fonction $g$ définie sur l'intervalle $[330;480]$ par $g(t)=0,0056t^2-6,1517t+4389$, $t$ étant exprimé en minutes.
1. Résoudre dans $\mathbb{R}$ l'équation : $0,0056t^2-6,1517t+4389 = 4389$
2. En utilisant les propriétés de symétrie de la parabole, déterminer l'axe de symétrie de la parabole représentant la fonction polynôme définie sur $\mathbb{R}$ par : $g(t)=0,0056t^2-6,1517t+4389$
3. En déduire les variations de la fonction $g$.
4. Comment évolue le nombre de levures sur l'intervalle $[330;480]$ ? Quel est le nombre de levures au bout de $8$ heures ? On arrondira le résultat à l'unité.
Exercice 15
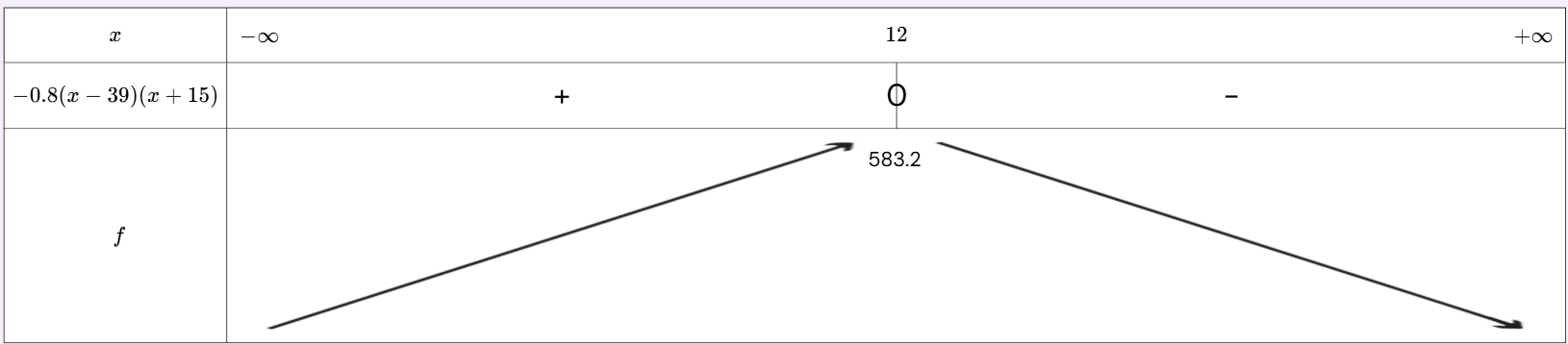
L'empreinte carbone est un indicateur des émissions de gaz à effet de serre qui intègre les émissions directes des ménages français, de la production nationale et celles associés aux produits importés. On étudie les émissions de $CO_2$ de la France selon l'empreinte carbone entre $1995$ et $2015$. Les émissions sont exprimés en million de tonnes équivalent $CO_2$ (Mt eq $CO_2$). On modélise l'évolution de ces émissions en fonction du temps écoulé depuis $1995$, exprimés en années, par la fonction $f$ définie sur l'intervalle $[0;39]$ par : $f(x)=-0,8x^2+19,2x+468$
1. Montrer que $f(x)=-0,8(x-39)(x+15)$. En déduire les deux racines du polynôme sur $\mathbb{R}$.
2. Déterminer le sens de variation de $f$ et dresser le tableau de variation de $f$ sur l'intervalle $[0;39]$.
3. La France s'est engagé, d'ici 2030, à réduire ses émissions de $CO_2$ de $40\%$ par rapport à leur niveau en $1995$, estimé à $468$ Mt eq $CO_2$. D'après ce modèle, l'engagement de la France sera-t-il tenu en $2030$ ? Justifier la réponse.
Exercice 16
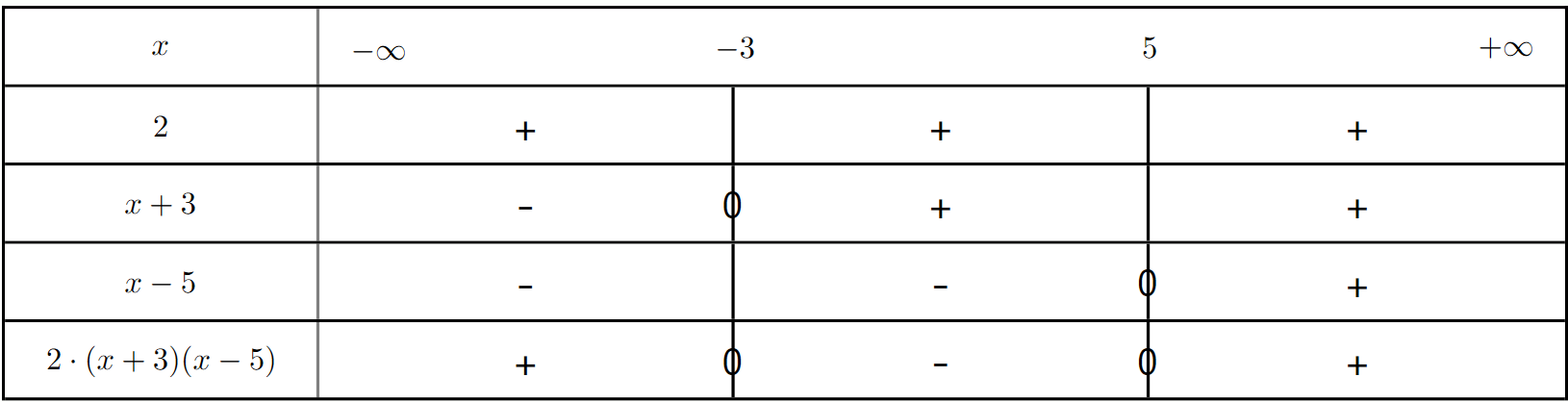
On considère la fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $h(x) = 2(x+3)(x-5)$.
1. Déterminer les racines de la fonction $h$.
2. Établir le tableau de signes de la fonction $h$ sur $\mathbb{R}$.
3. Résoudre graphiquement puis algébriquement l'inéquation $h(x) \leq 0$.
Exercice 17
Une entreprise fabrique et vend des montres connectées. Le coût de production de $x$ montres est donné par $C(x) = 0,1x^2 + 10x + 5000$ euros. Le prix de vente d'une montre est de $60$ euros.
1. Exprimer la recette $R(x)$ obtenue par la vente de $x$ montres.
2. Exprimer le bénéfice $B(x)$ réalisé par la vente de $x$ montres. Rappel : le bénéfice est la différence entre la recette et le coût de production.
Aide (complément de cours) : Pour une fonction quadratique de la forme $f(x) = ax^2 + bx + c$, l'abscisse du sommet (maximum ou minimum) est donnée par la formule $x = -b/2a$.
3. Déterminer le nombre de montres que l'entreprise doit vendre pour que le bénéfice soit maximal.
4. Calculer le bénéfice maximal.