Nombres dérivés et équation de tangente
Ici, vous trouverez des exercices pour vous entraîner sur les nombres dérivés et les équations de tangentes.
Revoyons ensemble les points essentiels sur les nombres dérivés et équation de tangente avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Introduction au nombre dérivé
Imaginez une courbe représentant une fonction. Le nombre dérivé $f'(a)$ en un point d'abscisse $a$ est un nombre qui indique la pente de la courbe en ce point précis. C'est comme mesurer à quel point la fonction monte ou descend exactement à cet endroit.
Graphiquement, $f'(a)$ est le coefficient directeur de la tangente à la courbe de $f$ au point d'abscisse $a$. La tangente est la droite qui "frôle" la courbe au plus près en ce point.
2. Taux de variation : la base du nombre dérivé
Pour comprendre le nombre dérivé, on commence par le taux de variation. C'est une mesure de combien la fonction change en moyenne entre deux points.
Si on prend deux points d'abscisses $a$ et $a+h$, le taux de variation de $f$ entre ces points est :
$$T(h) = \frac{f(a+h) - f(a)}{h}$$
Ce taux de variation représente la pente de la droite qui relie les deux points sur la courbe. C'est une pente moyenne entre les deux points.
Pour obtenir la pente exacte en un seul point (le nombre dérivé), on va rapprocher de plus en plus le point $a+h$ du point $a$. En faisant cela, le taux de variation va se rapprocher d'une valeur précise : le nombre dérivé.
3. Équation de la tangente
Une fois que l'on connaît le nombre dérivé $f'(a)$ en un point d'abscisse $a$, on peut trouver l'équation de la tangente en ce point. L'équation de la tangente à la courbe de $f$ au point d'abscisse $a$ est :
$$y = f'(a)(x-a) + f(a)$$
Pour construire cette équation, on a besoin de :
- $f'(a)$ : le nombre dérivé, qui est la pente de la tangente.
- $a$ : l'abscisse du point de tangence.
- $f(a)$ : l'ordonnée du point de tangence.
4. Fonction dérivable
On dit qu'une fonction $f$ est dérivable en $a$ si on peut trouver un nombre dérivé $f'(a)$ en ce point. Cela signifie que la courbe est "douce" au point d'abscisse $a$, et qu'on peut y tracer une tangente non verticale.
Si une fonction est dérivable en chaque point d'un intervalle, on dit qu'elle est dérivable sur cet intervalle.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
Soit $f$ une fonction définie sur $\mathbb{R}$ par $f(x)=x^2$.
1. Calculer le taux de variation de $f$ au point d'abscisses $2$.
2. En déduire le nombre dérivée de $f$ en $2$.
Exercice 2
Déterminer le taux de variation de la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=(x+1)^2$ au point d'abscisse $-2$. En déduire $f'(-2)$.
Exercice 3
Déterminer le taux de variation de la fonction inverse au point $1$. En déduire le nombre dérivé de la fonction inverse au point $1$.
Exercice 4
Soit $g$ la fonction définie sur $\mathbb{R}$ pour laquelle on a : $\dfrac{g(-2+h)-g(-2)}{h}=-5+h$ où $h$ est un nombre réel non nul. Déterminer $g'(-2)$.
Exercice 5
Soit $f$ la fonction définie sur $\mathbb{R}$ pour laquelle on a : $\dfrac{f(1+h)-f(1)}{h}=h^2+2h+2$ où $h$ est un nombre réel non nul. Déterminer $f'(1)$.
Exercice 6
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f \colon x \mapsto x^2+1$ et $h$ un nombre réel non nul.
1. Exprimer en fonction de $h$ le taux de variation entre $3$ et $3+h$.
2. En déduire que la fonction est dérivable en $3$ et déterminer $f'(3)$.
3. De la même manière, montrer que $f$ est dérivable en $-2$ et déterminer $f'(-2)$
Exercice 7
Soit $f$ la fonction définie sur $[0;+\infty[$ par $f \colon x \mapsto \sqrt{x}$
1. Calculer le taux de variation de $f$ en $1$
2. Vérifier que pour tout $h$ non nul supérieur à $-1$ : $\dfrac{\sqrt{1+h}-1}{h} = \dfrac{1}{\sqrt{1+h}+1}$
3. En déduire que la fonction est dérivable en $1$ et déterminer $f'(1)$.
4. Quelle est la limite du taux de variation de $f$ en $0$ ? Que peut-on en déduire ?
Exercice 8
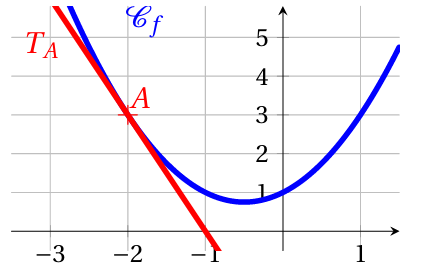
1. Lire graphiquement le coefficient directeur de $T_A$.
2. Quel nombre dérivé peut-on en déduire?
Exercice 9 - Cas 1
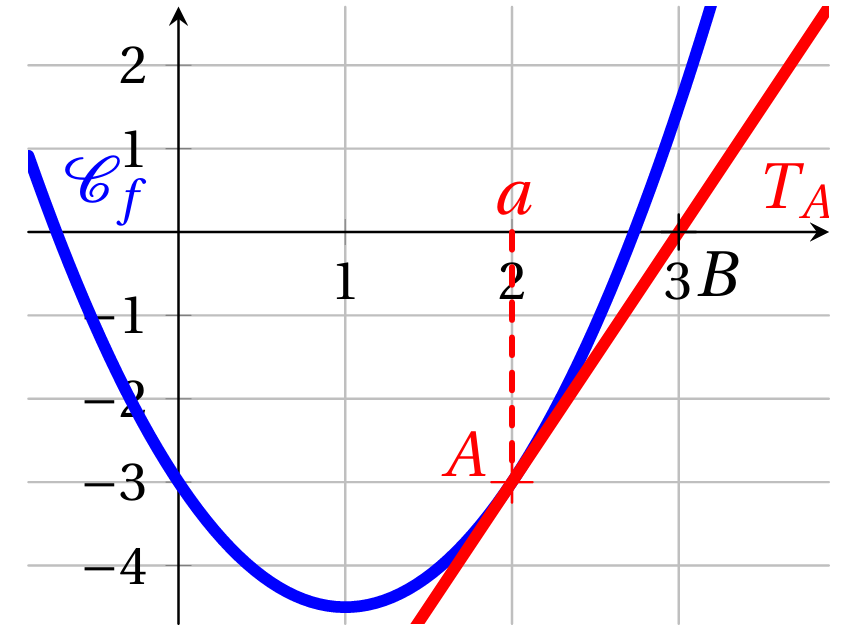
Cas 1.
Exercice 9 - Cas 2
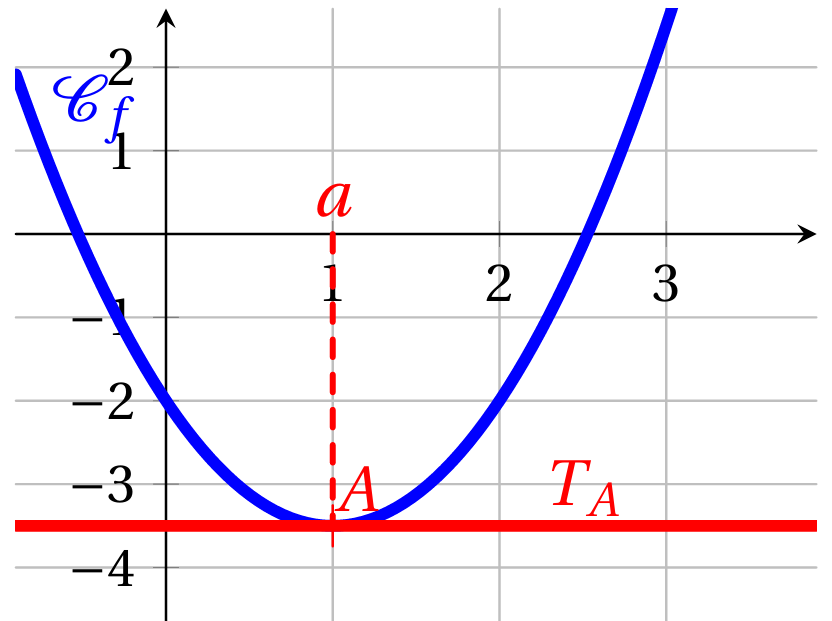
Cas 2.
Exercice 9 - Cas 3
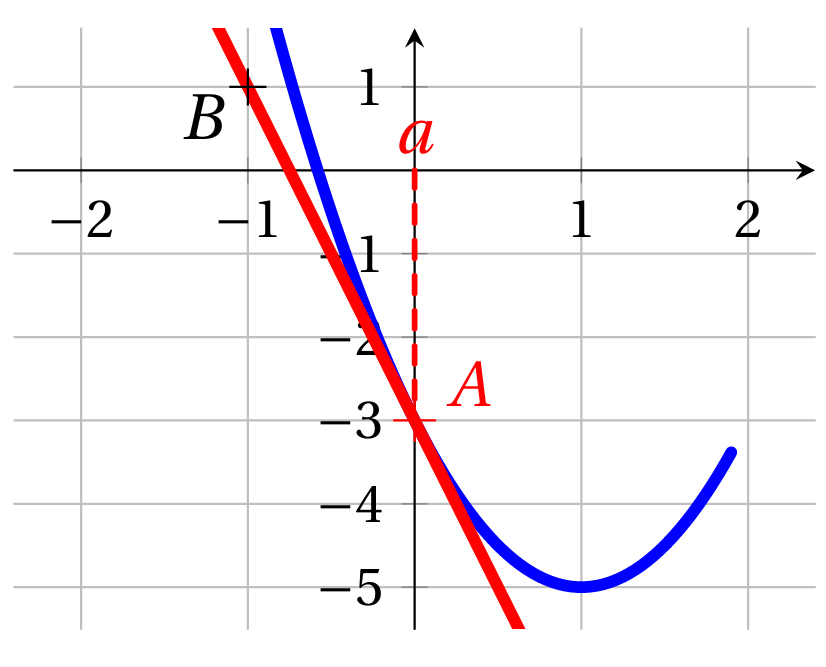
Cas 3.
Exercice 10
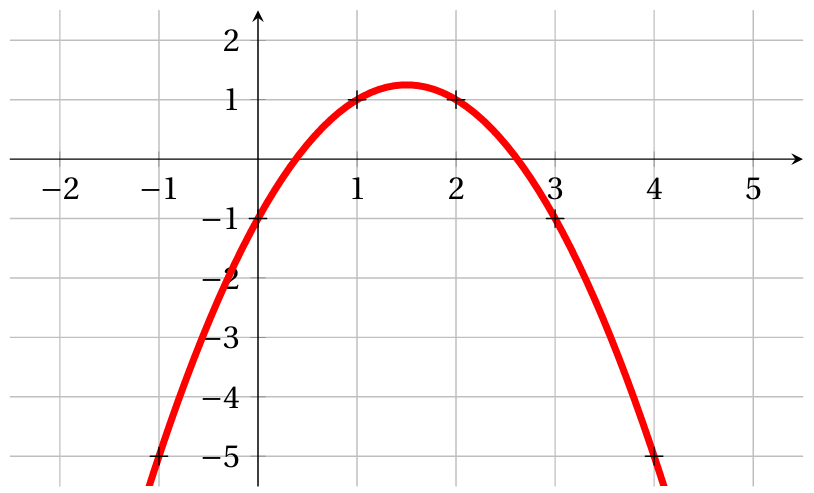
Tracer la tangente à $\mathcal{C}_f$ au point d'abscisse $2$ et la tangente à $\mathcal{C}_f$ au point d'abscisse $0$.
Exercice 12
Soit la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = x^2 – 4x + 6$. A l'aide de la calculatrice, déterminer $f(3)$, $f'(3)$ et en déduire l'équation réduite de la tangente $T$ à la courbe représentative de $f$ au point d'abscisse $3$.
Exercice 13 bis
On considère une fonction $g$ dérivable sur $\mathbb{R}$. On donne les informations suivantes :
- La valeur de la dérivée de $g$ au point d'abscisse $-2$ est $g'(-2) = 1$.
- La valeur de la dérivée de $g$ au point d'abscisse $1$ est $g'(1) = -3$.
- La valeur de la dérivée de $g$ au point d'abscisse $3$ est $g'(3) = 0.5$.
- La fonction $g$ passe par le point $A$ de coordonnées $(-2 ; 0)$, par le point $B$ de coordonnées $(1 ; 4)$ et par le point $C$ de coordonnées $(3 ; 2)$.
1. a. Rappeler l'interprétation du nombre dérivé $g'(a)$ pour une fonction $g$ et un nombre $a$.
b. Que représente la valeur $g'(-2) = 1$ pour la fonction $g$ au point d'abscisse $-2$ ?
2. Déterminer l'équation réduite de la tangente à la courbe représentative de $g$ au point d'abscisse $-2$.
3. Déterminer l'équation réduite de la tangente à la courbe représentative de $g$ au point d'abscisse $1$.
4. Déterminer l'équation réduite de la tangente à la courbe représentative de $g$ au point d'abscisse $3$.
Exercice 14
Soit $g$ une fonction dérivable sur $\mathbb{R}$. On a le tableau de valeurs suivant.
| $x$ | -3 | -1 | 0 | 2 | 4 | 5 |
|---|---|---|---|---|---|---|
| $g(x)$ | 6 | 0 | 2 | 4 | 3 | 1 |
| $g'(x)$ | -4 | 0 | 1,5 | 0 | -1 | -3 |
2. Construire en chacun de ces points les tangentes à la courbe $\mathcal{C}_g$ représentative de la fonction $g$.
3. Représenter une allure possible de $\mathcal{C}_g$.
Exercice 15
La courbe représentative d'une fonction $f$ admet une tangente au point d'abscisse $1$. Cette tangente a pour équation $y=-7x+9$. Que vaut $f'(1)$ ? Que vaut $f(1)$ ?
Exercice 16
Soit $g$ la fonction définie sur $\mathbb{R}$ par $g(x)=(2x^2 – 5x + 4)^{10}$. On admet que $g$ est dérivable en $1$, et que $g'(1)=-10$. Déterminer l'équation réduite de la tangente à la courbe représentative de $g$ au point d'abscisse $1$.
Exercice 17
Soit $f$ une fonction dérivable sur $\mathbb{R}$ et soit $\mathcal{C}$ sa courbe représentative dans un repère du plan. Le point $A(3;-1)$ appartient à la courbe $\mathcal{C}$. Sachant que la tangente $T$ à la courbe $\mathcal{C}$ au point $A$ passe par le point $J(0;1)$, déterminer $f'(3)$, puis l'équation de $T$.