Schéma de Bernoulli
Ici, vous trouverez une série d'exercices conçus pour vous aider à maîtriser le concept de schéma de Bernoulli, un outil fondamental en probabilités. Ces exercices vous guideront à travers l'identification des épreuves de Bernoulli, la détermination des paramètres clés, la construction d'arbres pondérés, et le calcul de probabilités dans divers contextes. Que vous soyez en Terminale Spécialité Maths ou que vous cherchiez à renforcer vos bases en probabilités, ces exercices sont faits pour vous !
Revoyons ensemble les points essentiels sur le Schéma de Bernoulli avant de démarrer les exercices. Ces rappels sont vos fondations pour réussir !
1. Épreuve de Bernoulli
Une épreuve de Bernoulli est une expérience aléatoire ne possédant que deux issues possibles, appelées généralement succès et échec.
On note souvent :
• S l'événement "succès"
• $\overline{S}$ l'événement "échec"
La probabilité d'obtenir un succès est notée $p = P(S)$, et la probabilité d'un échec est $1-p = P(\overline{S})$.
Exemple : Lancer une pièce de monnaie et regarder si elle tombe sur "face" est une épreuve de Bernoulli. Le succès pourrait être "obtenir face", et l'échec "obtenir pile".
2. Schéma de Bernoulli
Un schéma de Bernoulli est la répétition de $n$ épreuves de Bernoulli identiques et indépendantes.
Identiques signifie que la probabilité de succès $p$ reste la même à chaque épreuve.
Indépendantes signifie que le résultat d'une épreuve n'influence pas le résultat des épreuves suivantes.
Un schéma de Bernoulli est caractérisé par deux paramètres :
• n : le nombre de répétitions de l'épreuve.
• p : la probabilité de succès à chaque épreuve.
Exemple : Lancer 10 fois de suite une pièce de monnaie est un schéma de Bernoulli si on suppose que les lancers sont indépendants et que la pièce n'est pas truquée (probabilité de "face" constante à chaque lancer).
3. Arbre pondéré pour un schéma de Bernoulli
Un arbre pondéré est un outil graphique utile pour visualiser et calculer les probabilités dans un schéma de Bernoulli.
Chaque niveau de l'arbre représente une épreuve de Bernoulli.
Chaque branche est pondérée par la probabilité de l'issue correspondante (p pour le succès, 1-p pour l'échec).
Pour calculer la probabilité d'une séquence d'issues (un chemin dans l'arbre), on multiplie les probabilités le long des branches de ce chemin.
Exemple pour 3 épreuves :
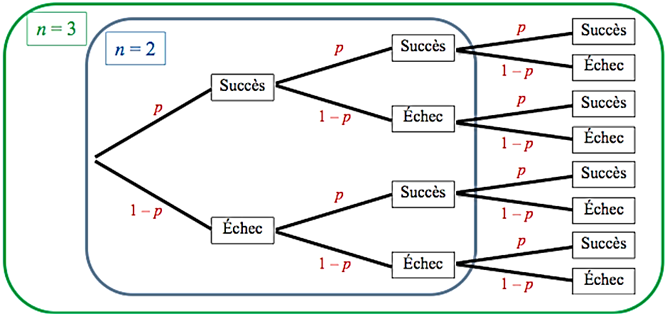
Sur cet arbre, p représente la probabilité de succès (S) et 1-p la probabilité d'échec (E) à chaque épreuve.
4. Calcul de probabilités dans un schéma de Bernoulli
Pour calculer la probabilité d'obtenir un nombre précis de succès dans un schéma de Bernoulli, on peut utiliser l'arbre pondéré pour lister tous les chemins possibles et calculer leurs probabilités.
Cependant, pour un grand nombre d'épreuves, il existe des formules plus efficaces (que vous verrez plus tard dans le cours, notamment avec la loi binomiale).
Pour l'instant, l'arbre pondéré et le calcul direct des probabilités des chemins sont les méthodes à privilégier pour les exercices de cette section.
Règle d'addition des probabilités : Pour calculer la probabilité d'un événement constitué de plusieurs chemins disjoints dans l'arbre (par exemple, "obtenir exactement un succès en 2 épreuves"), on additionne les probabilités de chaque chemin réalisant cet événement.
C'est noté ? 💪 Maintenant, place aux exercices ! Bonne chance !
Exercice 1
Pour chacune des expériences aléatoires suivantes dites si elle constitue une épreuve de Bernoulli? Si c'est le cas proposez un succès $S$ et sa probabilité $P(S)$.
1. Un stock contient $1\ \%$ de pièces défectueuses. On y prélève une pièce et on regarde si elle présente un défaut.
2. Selon l'INSEE, $45\ \%$ des familles française ont un seul enfant, $38\ \%$ en ont deux et $17\ \%$ en ont trois ou plus. On interroge au hasard un élève du lycée et on lui demande le nombre d'enfants de sa famille.
Exercice 2
Pour chaque expérience aléatoire dites si elle constitue un schéma de Bernoulli. Proposez dans ce cas les valeurs des paramètres $n$ et $p$.
1. Dans un stock de $20$ vis, dont $3$ sont trop longues, on prélève successivement $15$ vis, au hasard et sans remise. pour chacune on regarde si elle est trop longue ou non.
2. On considère une suite de $50$ lettres choisies de façon aléatoire. Pour chacune d'entre-elles, on regarde si elle est une voyelle ou non.
Exercice 3
Un appareil comporte deux composantes électroniques qui fonctionnent de façon indépendante. On suppose que, pour chacun d'eux, la probabilité de l'événement $P$ « le composant tombe en panne » est égale à $0,01$.
Démontrer que cette situation est un schéma de Bernoulli dont vous préciserez les paramètres.
Exercice 4
Un restaurateur constate qu'au déjeuner, $9$ clients sur $10$ prennent un café. Quatre clients se présentent pour déjeuner et commandent de façon indépendante. Pour chacun, on note $C$ l'événement « le client prend un café ».
Démontrer que cette situation est un schéma de Bernoulli dont vous préciserez les paramètres.
Exercice 5
Une urne contient trois boules: une rouge, une noire et une bleue. On tire une boule au hasard, on la remet dans l'urne, puis on tire une autre boule au hasard. On admet que tous les tirages d'une boule sont équiprobables.
1. Montrez en utilisant un arbre que la probabilité d'obtenir deux boules rouges $(RR)$ est $\frac{1}{9}$ et que la probabilité d'obtenir une boule rouge puis une boule qui ne l'est pas est $\frac{2}{9}$.
2. On s'intéresse maintenant, pour chaque tirage, à l'obtention ou non de la boule rouge et on représente la situation à l'aide de l'arbre ci-dessous, appelé « arbre pondéré ».
1. Que signifie $R$? $\overline{R}$?
2. À quelles probabilités correspondent les nombres $\frac{1}{3}$ et $\frac{2}{3}$ écrits sur les branches de l'arbre pondéré?
3. Déterminez la règle permettant , à partir de l'arbre pondéré, de calculer les probabilités obtenues à la question 1) et, plus généralement, les probabilités des quatre issues de ce dernier arbre.
Exercice 6
Un schéma de Bernoulli est représenté sous forme d'un arbre ci-dessous. Pour chaque épreuve de Bernoulli répétée, on a noté $S$ le succès et $E$ l'échec.
1. Précisez les valeurs de paramètres $n$ et $p$ du schéma de Bernoulli.
2. Calculez la probabilité des événements $SSE$, $SES$ et $ESS$. Que constate-t-on?
3. Même question pour $SEE$, $ESE$ et $EES$.
Exercice 7
On choisit au hasard une carte dans un jeu de 32 cartes et on s'intéresse à l'obtention d'un As. Puis on remet la carte dans le tas et on choisit une seconde carte.
1. Déterminer la probabilité d'obtenir un As.
2. Justifier que cette situation est un schéma de Bernoulli.
3. Écrire toutes les listes des résultats possibles.
4. On note A l'événement « Obtenir au moins un succès ».
Écrire les listes qui réalisent l'événement A.
Calculer la probabilité de chacune de ces listes et en déduire P(A).
Exercice 8
On lance un dé équilibré à six faces numérotées de 1 à 6. On note le numéro de la face supérieure obtenue. Soit $S$ l'événement « Obtenir un 6 » .
1. Donner la probabilité de l'événement S appelé succès et la probabilité de l'événement $\bar{S}$ appelé échec.
2. On répète deux fois l'expérience décrite ci-dessus. Justifier que cette situation est un schéma de Bernoulli.
3. Calculer la probabilité d'obtenir au moins un succès.
Exercice 9
Une urne contient trois boules blanches et deux boules bleues. On tire au hasard une boule de l'urne, on note sa couleur et on remet la boule dans l'urne. On note $S$ l'événement « Obtenir une boule blanche ».
1. Déterminer la probabilité de l'événement $S$ et celle de l'événement $\bar{S}$.
2. On répète trois fois l'expérience décrite ci-dessus. Justifier que cette situation est un schéma de Bernoulli.
3. Calculer la probabilité d'obtenir au moins un succès.
Exercice 10
Sur un trajet domicile-travail, Sofiane rencontre trois feux tricolores, indépendants les uns des autres. Il a remarqué que, statistiquement, chaque feu est au vert une fois sur trois.
1. Représenter la situation par un arbre pondéré.
2. Pour un trajet domicile-travail de Sofiane, calculez la probabilité des événements suivants.
1. Deux feux sur trois sont au vert.
2. Un seul feu sur les trois est au vert.
3. Tous les feux sont au vert.
4. Aucun des trois feu n'est au vert.
Exercice 11
Un carton de jouets contient un nombre très important de petites briques de couleur rouge ou bleue. On estime que la proportion de briques bleues est $40\ \%$.
Élise prend quatre briques au hasard dans le carton. On assimile ce prélèvement à un tirage successif avec remise.
1. Justifier que l'expérience est un schéma de Bernoulli.
2. Modélisez la situation à l'aide d'un arbre pondéré.
3. Calculez la probabilité des événements suivants.
1. Élise à prélevé $4$ briques bleues.
2. Élise a prélevé deux briques bleues, puis deux briques rouges.
3. Élise a prélevé au moins une brique bleue.
4. Élise a prélevé au plus une brique rouge.
Exercice 12
David a du mal à entendre son réveil le matin. Ses parents estiment que, $6$ fois sur $10$, il se rendort et arrive en retard au lycée.
On suppose que les réveils de David sont indépendants d'un matin à l'autre et on étudie son comportement sur trois jours de la semaine (lundi, mardi, mercredi).
Nous noterons $R$ l'événement « David se rendort et est en retard au lycée », représenter la situation par un arbre pondéré.
1. Justifiez que cette situation correspond à un schéma de Bernoulli.
2. Représentez la situation par un arbre pondéré.
3. Calculez la probabilité des événements suivants:
1. David n'est pas en retard les trois jours.
2. David est en retard au lycée le lundi et le mardi matins.
3. David est en retard deux matins consécutifs.
4. David est en retard au plus une fois.
Exercice 13
Bernard est un adepte de ball-trap. Il tire successivement sur dix disques (les résultats des dix tirs sont indépendants les uns des autres). Pour chaque tire la probabilité que Bernard atteigne le disque est égale à 0,6.
| A | B | C | D | .... E | |
| 1 | L'expérience : | ||||
| 2 | est une épreuve de Bernoulli dont le succès est l'événement : | ||||
| 3 | La probabilité de succès est : | ||||
| 4 | Cette épreuve est répétée : | ||||
| 5 | de façon identique et indépendante. il s'agit donc d'un schéma de Bernoulli de paramètres : | n= | et | p= | |
| 6 | |||||
| 7 | Nombre aléatoire entre 0 et 1 : | ||||
| 8 | |||||
| 9 | Issue d'une simulation de tir au ball-trap |
1. Complétez les cellules du tableur expliquant pourquoi on a un schéma de Bernoulli en précisant ses paramètres:
1. Décrivez en B1 l'expérience que l'on conservera comme épreuve de Bernoulli.
2. Écrivez en B2 une phrase décrivant ce qu'est un succès pour cette épreuve de Bernoulli.
3. Donnez en B3 la probabilité d'un succès.
4. Indiquez en B4 le nombre de fois qu'est répétée cette épreuve.
5. Complétez les égalités en B5 et D5.
2. Le tableur génère des nombres aléatoires compris entre 0 et 1 avec la commande:
=ALEA()
Entrez cette commande en cellule B7, puis appuyer plusieurs fois sur la touche F9.
3. Le test conditionnel sur le tableur se fait avec la commande "SI".
1. Entrez en cellule F4:
=SI(B3=10;"vrai";"faux")
puis expliquez le rôle de cette commande.
2. En combinant les fonctions SI et ALEA du tableur entrez en B9 une formule simulant le tir de ball-trap et affichant Succès ou Échec.
4. Simulez avec le tableur les 10 tirs de ball-trap en usant de la poignée de recopie jusqu'à B19.
5. Dans un schéma de Bernoulli ce qui nous intéresse c'est le nombre de succès obtenus. Pour cela entrez en B20 la commande:
=NB.SI(B9:B19;"Succès")
appuyez plusieurs fois sur F9 puis expliquez son rôle.